递归算法经典例题
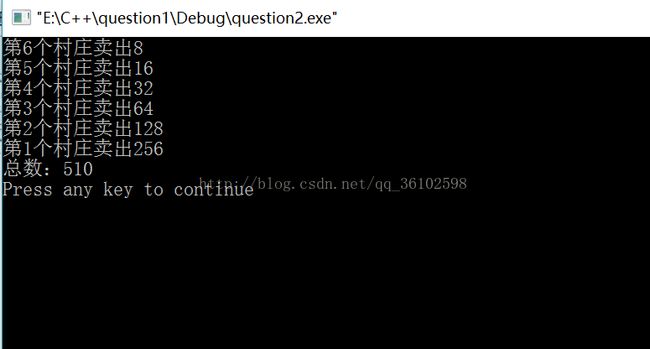
1、一个人赶着鸭子去每个村庄卖,每经过一个村子卖去所赶鸭子的一半又一只。这样他经过了七个村子后还剩两只鸭子,问他出发时共赶多少只鸭子?经过每个村子卖出多少只鸭子
题目分析:
递归终止的条件是当达到第7个村庄时递归停止,设经过的村庄数为n则有剩余的鸭子为总数为每次剩余的鸭子数位sum = sum-(sum/2+1)
算法构造:当 n=7 时 sum = 2;当 0
程序源代码:
/**
*递归解决赶鸭子问题
*anthor :zw_com
*时间 : 2017/05/13
*/
#include
class Questionone{
public:
int answer(int n, int sum){
if(n>0){
sum = 2*sum+2;
if(n-1>0){
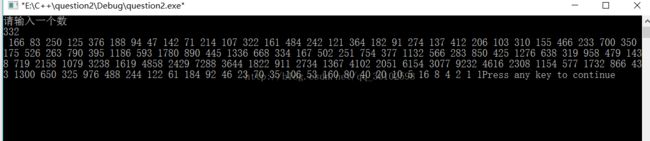
cout<<"第"< 2、角谷定理。输入一个自然数,若为偶数,则把它除以2,若为奇数,则把它乘以3加1。经过如此有限次运算后,总可以得到自然数值1。求经过多少次可得到自然数1。
算法分析:
递归的终止条件是最后值为1;设输入的值为n先进项判断,若 n = 1则输出n;
若n不为1;则对他进行偶数判断,若为偶数除2,若为奇数则乘3加1;然后在进行偶数判断,直到n = 1为止;
算法构造
n=1 时 输出n;n!=1时 偶数判断 偶数 n = n/2;若是奇数 n = 3*n+1
源代码:
/**
*递归算法角谷定理
*anthor zw_com
*时间 2017/05/13
**/
#include
class questiontwo{
public:
int answer(int sum){
if(sum == 1){
cout<<" "<>c;
questiontwo question2;
question2.answer(c);
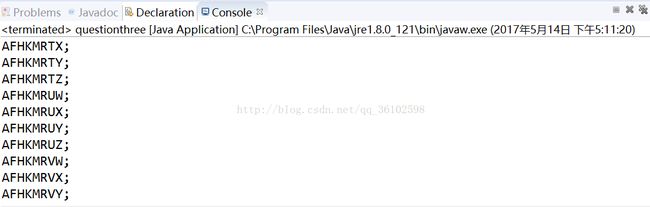
} 1. 电话号码对应的字符组合:在电话或者手机上,一个数字如2对应着字母ABC,7对应着PQRS。那么数字串27所对应的字符的可能组合就有3*4=12种(如AP,BR等)。现在输入一个3到11位长的电话号码,请打印出这个电话号码所对应的字符的所有可能组合和组合数。
题目分析:根据题意可知:2对应的是ABC 3对应的是DEF 4对应的是GHI 5对应的是JKL
6对应的是MNO 7对应的是PQRS 8对应的是TUV 9对应的是WXYZ
源程序:
/**
* 用递归的方法解决电话号码对应的字符组合
* @author ZW_COM
* 时间: 2017/05/14
*/
public class questionthree {
/**
*
* @param number 电话号码
* @param answer 辅助数组
* @param index 电话位数中对应的第几位循环
* @param n 电话位数
*/
public static void Answer(int []number, int []answer,int index,int n){
char[][] word ={{},{},{'A','B','c'},{'D','E','F'},{'G','H','I'},{'J','K','L'},{'M','N','O'},{'P','Q','R','s'},{'T','U','V'},{'W','X','Y','Z'}};
int []sum = {0,0,3,3,3,3,3,4,3,4};
if(index == n){
for(int i = 0; i1. 日本著名数学游戏专家中村义作教授提出这样一个问题:父亲将2520个桔子分给六个儿子。分完 后父亲说:“老大将分给你的桔子的1/8给老二;老二拿到后连同原先的桔子分1/7给老三;老三拿到后连同原先的桔子分1/6给老四;老四拿到后连同原先的桔子分1/5给老五;老五拿到后连同原先的桔子分1/4给老六;老六拿到后连同原先的桔子分1/3给老大”。结果大家手中的桔子正好一 样多。问六兄弟原来手中各有多少桔子?
题目分析:解决此问题主要使用递归运算。由题目可以看出原来手中的加上得到的满足关系式:StartNum = 420 * (n -2)/(n - 1) 分给下一个人的橘子数:GiveNum = AfterGetNum / n; 下一个人的橘子数:nextStartNum = 420*(n-1)/(n-2) - GiveNum; 下一个人加上之前得到的橘子的总数:afterGetNum = nextStartNum + GiveNum; 以此使用递归算法可以算出各个孩子原来手中的橘子数。
源代码:
package question4;
/**
* 递归算法分桔子的问题
* @author zw_com
* 时间 :2017/05/14
*/
public class questionfour {
/**
*
* @param n 表示第几个儿子
* @param befor 表示为分配之前就的桔子数
* @param After 表示分配之后的桔子数
* @param m 分配的比例
* @return
*/
public int answer(int n,int befornum, int afternum,int m ){
if(n>6){
return 0;
}else{
System.out.println("老"+n+"原有的桔子数"+befornum);
//分给下一个人的桔子数
int givenum = afternum/m;
//下一个人的桔子数
int nextBeforenum = 420*(m-1)/(m-2)-givenum;
//下一人加上之前的桔子数的总数
int afterGetnum = nextBeforenum+givenum;
return answer(n+1,nextBeforenum,afterGetnum,m-1);
}
}
public static void main(String[] args){
questionfour question4 = new questionfour();
question4.answer(1, 240, 240, 8);
}