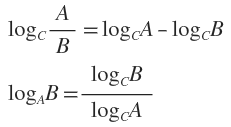分类算法之决策树ID3详解
(1)数据是怎么分裂的
(2)如何选择分类的属性
(3)什么时候停止分裂
从上述三个问题出发,以实际的例子对ID3算法进行阐述。
先上问题吧,我们统计了14天的气象数据(指标包括outlook,temperature,humidity,windy),并已知这些天气是否打球(play)。如果给出新一天的气象指标数据:sunny,cool,high,TRUE,判断一下会不会去打球。
table 1
| outlook | temperature | humidity | windy | play |
| sunny | hot | high | FALSE | no |
| sunny | hot | high | TRUE | no |
| overcast | hot | high | FALSE | yes |
| rainy | mild | high | FALSE | yes |
| rainy | cool | normal | FALSE | yes |
| rainy | cool | normal | TRUE | no |
| overcast | cool | normal | TRUE | yes |
| sunny | mild | high | FALSE | no |
| sunny | cool | normal | FALSE | yes |
| rainy | mild | normal | FALSE | yes |
| sunny | mild | normal | TRUE | yes |
| overcast | mild | high | TRUE | yes |
| overcast | hot | normal | FALSE | yes |
| rainy | mild | high | TRUE | no |
这个问题当然可以用朴素贝叶斯法求解,分别计算在给定天气条件下打球和不打球的概率,选概率大者作为推测结果。
现在我们使用ID3归纳决策树的方法来求解该问题。
预备知识:
(1)信息熵

补充两个对数去处公式:
(2) 信息增益
用决策树来预测:
决策树的形式类似于“如果天气怎么样,去玩;否则,怎么着怎么着”的树形分叉。那么问题是用哪个属性(即变量,如天气、温度、湿度和风力)最适合充当这颗树的根节点,在它上面没有其他节点,其他的属性都是它的后续节点。
那么借用上面所述的能够衡量一个属性区分以上数据样本的能力的“信息增益”(Information Gain)理论。
如果一个属性的信息增益量越大,这个属性作为一棵树的根节点就能使这棵树更简洁,比如说一棵树可以这么读成,如果风力弱,就去玩;风力强,再按天气、温度等分情况讨论,此时用风力作为这棵树的根节点就很有价值。如果说,风力弱,再又天气晴朗,就去玩;如果风力强,再又怎么怎么分情况讨论,这棵树相比就不够简洁了。
用熵来计算信息增益:
1 计算分类系统熵 类别是 是否出去玩。取值为yes的记录有9个,取值为no的有5个,即说这个样本里有9个正例,5 个负例,记为S(9+,5-),S是样本的意思(Sample)。那么P(c1) = 9/14, P(c2) = 5/14
这里熵记为Entropy(S),计算公式为:
Entropy(S)= -(9/14)*log2(9/14)-(5/14)*log2(5/14)
2 分别以Wind、Humidity、Outlook和Temperature作为根节点,计算其信息增益 我们来计算Wind的信息增益
当Wind固定为Weak时:记录有8条,其中正例6个,负例2个;
同样,取值为Strong的记录6个,正例负例个3个。我们可以计算相应的熵为:
Entropy(Weak)=-(6/8)*log(6/8)-(2/8)*log(2/8)=0.811 Entropy(Strong)=-(3/6)*log(3/6)-(3/6)*log(3/6)=1.0
现在就可以计算出相应的信息增益了:
所以,对于一个Wind属性固定的分类系统的信息量为 (8/14)*Entropy(Weak)+(6/14)*Entropy(Strong)
Gain(Wind)=Entropy(S)-(8/14)*Entropy(Weak)-(6/14)*Entropy(Strong)=0.940-(8/14)*0.811-(6/14)*1.0=0.048
这个公式的奥秘在于,8/14是属性Wind取值为Weak的个数占总记录的比例,同样6/14是其取值为Strong的记录个数与总记录数之比。
同理,如果以Humidity作为根节点: Entropy(High)=0.985 ; Entropy(Normal)=0.592 Gain(Humidity)=0.940-(7/14)*Entropy(High)-(7/14)*Entropy(Normal)=0.151 以Outlook作为根节点: Entropy(Sunny)=0.971 ; Entropy(Overcast)=0.0 ; Entropy(Rain)=0.971 Gain(Outlook)=0.940-(5/14)*Entropy(Sunny)-(4/14)*Entropy(Overcast)-(5/14)*Entropy(Rain)=0.247 以Temperature作为根节点: Entropy(Cool)=0.811 ; Entropy(Hot)=1.0 ; Entropy(Mild)=0.918 Gain(Temperature)=0.940-(4/14)*Entropy(Cool)-(4/14)*Entropy(Hot)-(6/14)*Entropy(Mild)=0.029 这样我们就得到了以上四个属性相应的信息增益值: Gain(Wind)=0.048 ;Gain(Humidity)=0.151 ; Gain(Outlook)=0.247 ;Gain(Temperature)=0.029 最后按照信息增益最大的原则选Outlook为根节点。子节点重复上面的步骤。这颗树可以是这样的,它读起来就跟你认为的那样:
ID3优点是理论清晰、方法简单、学习能力较强,但也存在一些缺点:
(1)只能处理分类属性的数据,不能处理连续的数据;
(2)划分过程会由于子集规模过小而造成统计特征不充分而停止;
(3)ID3算法在选择根节点和各内部节点中的分支属性时,采用信息增益作为评价标准。信息增益的缺点是倾向于选择取值较多的属性,在有些情况下这类属性可能不会提供太多有价值的信息。