tensorflow conv2d()参数解析
定义:
tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, data_format=None, name=None)
功能:将两个4维的向量input(样本数据矩阵)和filter(卷积核)做卷积运算,输出卷积后的矩阵
input的形状:[batch, in_height ,in_width, in_channels]
batch: 样本的数量
in_height :每个样本的行数
in_width: 每个样本的列数
in_channels:每个样本的通道数,如果是RGB图像就是3
filter的形状:[filter_height, filter_width, in_channels, out_channels]
filter_height:卷积核的高
filter_width:卷积核的宽
in_channels:输入的通道数
out_channels:输出的通道数
比如在tensorflow的cifar10.py文件中有句:

卷积核大小为 5*5,输入通道数是3,输出通道数是64,即这一层输出64个特征
在看cifar10.py里第二层卷积核的定义:
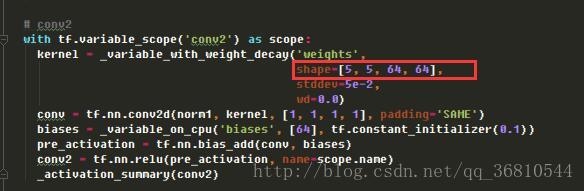
大小依然是5*5,出入就是64个通道即上一层的输出,输出依然是64个特征
strides:[1,stride_h,stride_w,1]步长,即卷积核每次移动的步长
padding:填充模式取值,只能为”SAME”或”VALID”
卷积或池化后的节点数计算公式:
output_w = int((input_w + 2*padding - filter_w)/strid_w) + 1
举例说明:
假设这里使用的图像每副只有一行像素一通道,共3副图像
>>> a = np.array([[1,1,1],[2,2,2],[3,3,3]])
>>> b=tf.reshape(a,[a.shape[0],1,a.shape[1],1])
>>> init = tf.initialize_all_variables()
>>> sess.run(init)
>>> sess.run(b)
array([[[[1],
[1],
[1]]],
[[[2],
[2],
[2]]],
[[[3],
[3],
[3]]]])
然后设有2个1*2的卷积核
>>> k=tf.constant([[[[ 1.0, 1.0]],[[2.0, 2.0]]]], dtype=tf.float32)
>>> mycov=tf.nn.conv2d(b, k, [1, 1, 1, 1], padding='SAME')
>>> init = tf.initialize_all_variables()
>>> sess.run(init)
>>> sess.run(mycov)
array([[[[ 3., 3.],
[ 3., 3.],
[ 1., 1.]]],
[[[ 6., 6.],
[ 6., 6.],
[ 2., 2.]]],
[[[ 9., 9.],
[ 9., 9.],
[ 3., 3.]]]], dtype=float32)
>>> sess.run(b)
array([[[[ 1.],
[ 1.],
[ 1.]]],
[[[ 2.],
[ 2.],
[ 2.]]],
[[[ 3.],
[ 3.],
[ 3.]]]], dtype=float32)
>>> sess.run(k)
array([[[[ 1., 1.]],
[[ 2., 2.]]]], dtype=float32)

最后的0是函数自动填充的,所以最后就得到了一个2通道的卷积结果
将k改成[[ 1.0, 0.5],[2, 1]]然后再次运行:
>>> k=tf.constant([[[[ 1.0, 0.5]],[[2, 1]]]], dtype=tf.float32)
>>> mycov=tf.nn.conv2d(b, k, [1, 1, 1, 1], padding='SAME')
>>> init = tf.initialize_all_variables()
>>> sess.run(init)
>>> sess.run(mycov)
array([[[[ 3. , 1.5],
[ 3. , 1.5],
[ 1. , 0.5]]],
[[[ 6. , 3. ],
[ 6. , 3. ],
[ 2. , 1. ]]],
[[[ 9. , 4.5],
[ 9. , 4.5],
[ 3. , 1.5]]]], dtype=float32)
卷积核一般用tf.get_variable()初始化,这里为了演示直接指定为常量