逆序对总结 【各种求法】

原文链接
.

逆序对：设 A 为一个有 n 个数字的有序集 (n>1)，其中所有数字各不相同。如果存在正整数 i, j 使得 1 ≤ i < j ≤ n 而且 A[i] > A[j]，则 A[i], A[j]> 这个有序对称为 A 的一个逆序对，也称作逆序数。

Example ：求给出一个由n个数组成的序列，求出该序列 的逆序对总数目
暴力解法这里就不提了。

思路 归并排序：（即使序列存在相同元素，该算法也适用，且代码不用修改）
归并排序是将数列a[l,h]分成两半a[l,mid]和a[mid+1,h]分别进行归并排序，然后再将这两半合并起来。在合并的过程中（设l<=i<=mid ,mid+1<=j<=h),
当a[i]<=a[j]时，并不产生逆序数；当a[i]>a[j]时，在前半部分中比a[i]大的数都比a[j]大，将a[j]放在a[i]前面的话，逆序数要加上mid+1-i。因此，可以在归并
排序中的合并过程中计算逆序数.

代码 实现一 归并排序

#include
#define LL long long
using namespace std;
const int MAXN = 50000+5;
const int MAXM = 1e5;
int a[MAXN],temp[MAXN];
LL ans=0;
int n;
void merge(int le,int mid,int ri){//使每两部分【都已经分别有序】，合并为一个有序集合 
    int i,j,k;
    // le到mid 是一个有序部分，mid+1到ri是一个有序部分 ，合并就行了  
    i=le;j=mid+1;k=le;
    for(;i<=mid&&j<=ri;){
        if(a[i]>a[j]){
            temp[k++]=a[j++];
            ans+=mid-i+1;
        }else  temp[k++]=a[i++];
    }
    while(i<=mid) temp[k++]=a[i++];
    while(j<=ri) temp[k++]=a[j++];
    for(i=le;i<=ri;i++) a[i]=temp[i];
}
void merge_sort(int le,int ri){//不断的分为一半，来使各个部分非递减有序 
    if(leint  mid=(le+ri)>>1;
        merge_sort(le,mid);
        merge_sort(mid+1,ri);
        merge(le,mid,ri);
    }
}
int main(){
    while(~scanf("%d",&n)){
        for(int i=0;iscanf("%d",&a[i]);
        ans=0;
        merge_sort(0,n-1);
        printf("%lld\n",ans);
    }
    return 0;
}

思路 二叉树：（我们先说序列不存在相同元素的情况，存在相同元素的情况后面补充）
1,初始化所有节点对应区间为0；
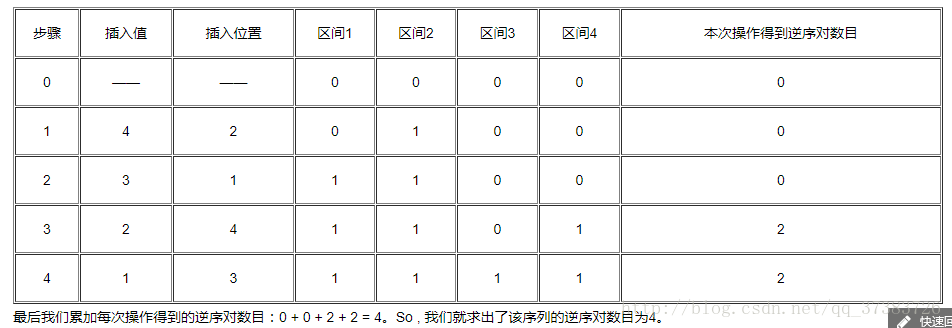
2,优先插入最大值，我们假设当前插入位置为pos，更新pos对应的区间为1。在每次插入后统计在pos位置之前有多少个数，说白了就是求 1到pos-1 区间 的数值总和；
3,累加每次插入的统计值，即是所求的当前序列的逆序对总数目。

struct record
{
    int val;//记录数值  
    int pos;//记录该数值在序列的位置 
}num[];
bool cmp(record a,record b)//优先数值大的 
{
    return a.val > b.val;
}

代码实现二–>线段树：
我们可以从大到小排序原序列，然后依次插入线段树的相应位置，每插入一次，判断一下它前面有几个数，这时候逆序数就加相应个数。
【线段树可以理解将每一个点作为值1，在判断一个数前面有几个数的时候，我们求一下从节点1到当前节点前一个，的总和就代表前面有几个数。】

#include
using namespace std;
#define LL long long
#define ll o<<1
#define rr o<<1|1
#define lson o<<1,le,mid
#define rson o<<1|1,mid+1,ri
const int MAXN =50000+10;
const int MAXM = 1e6;
const LL mod = 9973;
struct Tree{
    int l,r;
    int sum;
}tree[MAXN<<2];
int n;
struct Node{
    int id,val;
}node[MAXN];
bool cmp(Node a,Node b){
    return a.val>b.val;
}
void pushup(int o){
    tree[o].sum=tree[ll].sum+tree[rr].sum;
}
void build(int o,int le,int ri){
    tree[o]={le,ri,0};
    if(le==ri)  return ;
    int mid=(le+ri)>>1;
    build(lson);
    build(rson);
    pushup(o);
}
void update(int o,int pos,int val){
    if(tree[o].l==tree[o].r&&tree[o].l==pos){
        tree[o].sum+=val;
        return ;
    }
    int mid=(tree[o].l+tree[o].r)>>1;
    if(pos>mid) update(rr,pos,val);
    else if(pos<=mid) update(ll,pos,val);
    pushup(o);
}
int query(int o,int le,int ri){
    if(tree[o].l>=le&&tree[o].r<=ri) return tree[o].sum;
    int mid=(tree[o].l+tree[o].r)>>1;
    if(le>mid) query(rr,le,ri);
    else if(ri<=mid) query(ll,le,ri);
    else return  query(ll,le,mid)+query(rr,mid+1,ri);
}
int main(){
     int n,i;
     LL ans;
    while(scanf("%d",&n)!=EOF){
        build(1,1,n);
        for(int i=0;iscanf("%d",&node[i].val);
            node[i].id=i+1;
        }
        sort(node,node+n,cmp);
        ans=0;
        for(int i=0;i1,node[i].id,1);
            if(node[i].id==1)  continue;
            ans+=query(1,1,node[i].id-1);
        }
        printf("%lld\n",ans);
    }
    return 0;
}

代码实现三 –>树状数组：

#include 
#include 
#include 
#define MAX 500000
#define LL long long 
using namespace std;
int c[MAX];
int n;
struct record
{
    int val, pos;//记录数值 和 位置 
}num[MAX];
bool cmp(record a,record b)
{
    return a.val > b.val;
}
int lowbit(int x)
{
    return x&(-x);
}
int sum(int x)//求和 
{
    int s = 0;
    while(x > 0)
    {
        s += c[x];
        x -= lowbit(x);
    }
    return s;
}
void update(int x)//更新 
{
    while(x <= n)
    {
        c[x] += 1;
        x += lowbit(x); 
    }
}
int main()
{
    int i, j;
    LL ans;//统计总数目 
    while(scanf("%d", &n), n)
    {
        memset(c, 0, sizeof(c));//初始化 
        for(i = 0;i < n; i++)
        {
            scanf("%d", &num[i].val);
            num[i].pos = i + 1;
        }
        sort(num, num+n, cmp);
        ans = 0;
        for(i = 0;i < n; ++i)//每一次插入当前最大值 
        {
            update(num[i].pos);
            ans += sum(num[i].pos-1);//统计前面有多少个数 
        }
        printf("%lld\n", ans);
    }
    return 0;
}

补充存在相同元素情况：
上面代码实现的是序列不存在相同元素的情况，若是存在相同元素，只需限制一下插入顺序就ok了。
修改代码如下（其余代码不用修改）：

struct record
{
    int val;
    int pos;
}num[];
bool cmp(record a, record b)
{
    if(a.val != b.val)
    return a.val > b.val;
    else
    return a.pos > b.pos;
}