最长上升子序列(Longest Increasing Subsequence)问题(两种解法)

前言

本篇博客主要介绍了有关最长上升子序列(LIS)的三种DP解决方法,分别是O(n^2)和O(nlogn)(贪心加二分)两种DP

问题介绍

对于一个有序序列 x1,x2,x3,...,xn x 1 , x 2 , x 3 , . . . , x n 我们可以从其中得到一序列 ai1,ai2,ai3,...,aim a i 1 , a i 2 , a i 3 , . . . , a i m 满足 ai1<ai2<ai3<...<aim a i 1 < a i 2 < a i 3 < . . . < a i m 且 1≤i1<i2<i3<...<im≤n 1 ≤ i 1 < i 2 < i 3 < . . . < i m ≤ n 这样的字序列被称为该序列的上升子序列,也称单调递增子序列,而我们目标就是求一个序列中最长的单调递增的子序列。
如对于一有序序列{1,6,2,5,4,2,1,6},{1,5,6}为其一的上升子序列,而{1,2,4,6}就为其最长上升子序列.

求解方法

1. O(n2) O ( n 2 ) 朴素算法

那么既然这是一道DP问题,我们可以发现它具有无后效性和最优子结构,因为它这个序列首先不会改变,而对于它的子序列求出的LIS会也会对答案有贡献。
那么f[i]定义为：以 xi x i 结尾的最长上升子序列的长度
我们首先可以发现,单个位置的f[i]肯定为1因为它可以以自己作为一[1,i]的上升子序列
然后我们假设f[1],f[2],…,f[i-1]的值都已求出,而我们的目标就是求f[i]的值.也就是要求状态转移方程式.
我们现在已知道在1~j(1<=j< i)的最长上升子序列,我们的目标就是在一合法的1~j且该子序列的LIS最长的后添加一i,那是不是如果 xj<xi x j < x i 就可以进行拼接？也就是转移。那我们就可以得到状态转移方程式;

f[i]=max(f[j])+1(1<=j<iandxj<xi) f [ i ] = m a x ( f [ j ] ) + 1 ( 1 <= j < i a n d x j < x i )

最后答案就是f[n]

代码

#include
#include
#define LL long long
using namespace std;
int read(){
    int f=1,x=0;char s=getchar();   
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}  
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
#define MAXN 1000
int x[MAXN+5],f[MAXN+5];
int main()
{
    int n=read(),ans=1;
    for(int i=1;i<=n;i++)
        x[i]=read();
    for(int i=1;i<=n;i++){
        f[i]=1;
        for(int j=1;j<=i-1;j++)
            if(x[j]1>f[i])
                f[i]=f[j]+1;
        ans=max(ans,f[i]);
    }
    printf("%d\n",ans);
    return 0;
}

2. O(n⋅logn) O ( n · l o g n ) 贪心+二分优化

我们的状态定义就会变得跟之前的不一样了,但我们还是可以通过刚才的定义来观察一下：
我们对于 i i 将会找到它之前满足条件的最大的f[j]转移过来也就是长度最大,那其实我们可以来建一个一长度为下标的数组f,我们的目标是每次能直接将low数组中小于i的最大的一个下标直接加1就能得到1~i中以i结尾的最长的LIS,f[i]在这里定义为：
f[i]:长度为i的上升子序列中末尾元素的最小值 f [ i ] : 长 度 为 i 的 上 升 子 序 列 中 末 尾 元 素 的 最 小 值
因为这样是一贪心策略,对于一定位置i,当一上升子序列长度一定是,末尾元素越小越利于后面元素的选择
也就是大于等于i的第一个数的下标,同时由于这里i在这里必然小于f[i]还可以顺带更新f[i]，我们这样做了过后整个f数组是呈严格上升的,于是我们就能直接二分答案,在这里我们可以直接调用algoriethm里的lower_bound函数,二分一次low数组的时间复杂度的 O(logn) O ( l o g n ) ，所以总的时间复杂度是 O(n⋅logn) O ( n · l o g n )
来一次完整演示：
这是原数组

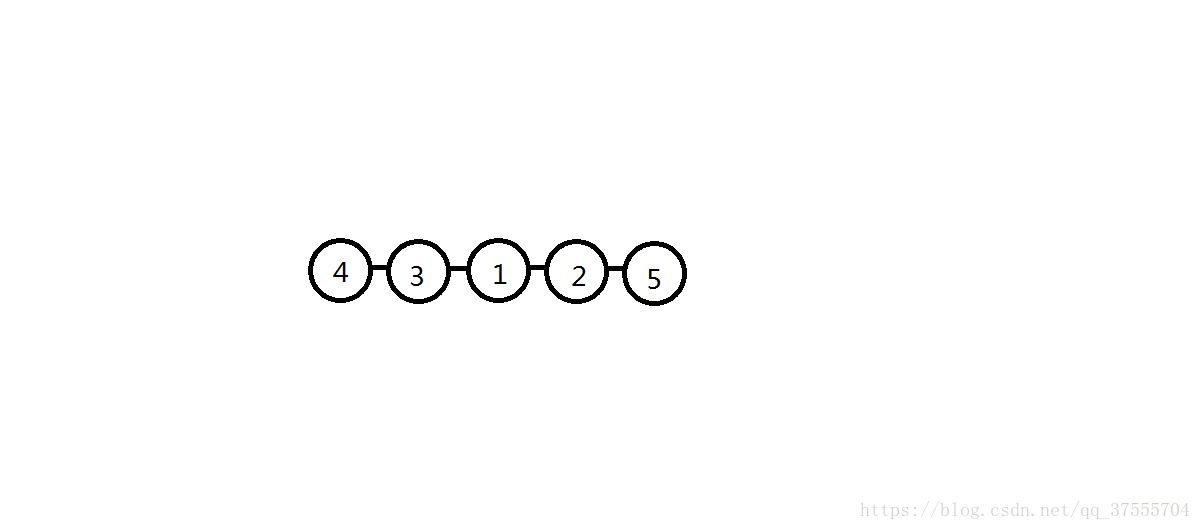
首先将f[1]更新

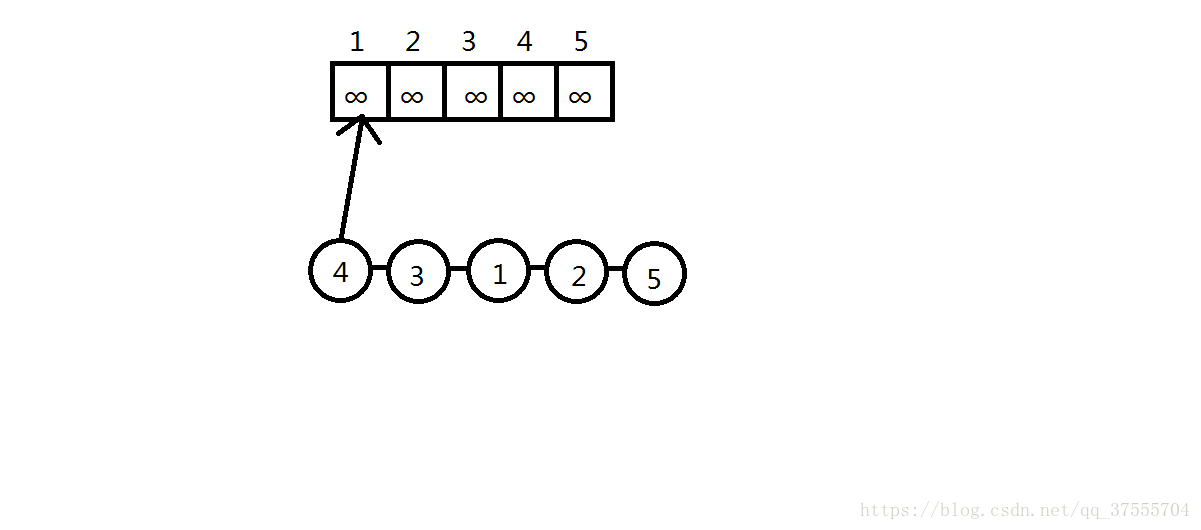
然后发现f[1]还是比当前元素大,继续更新

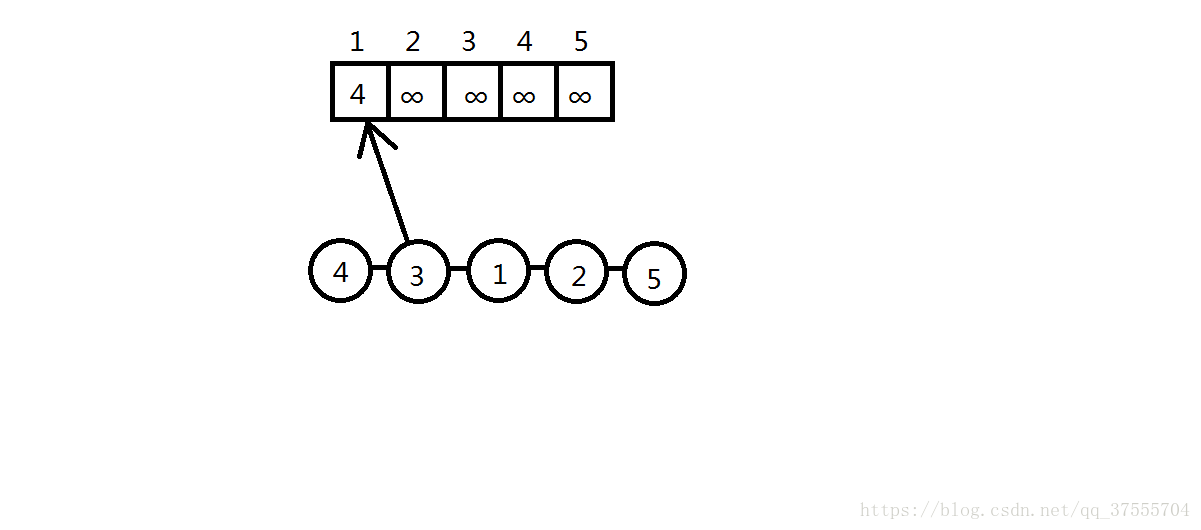
同上

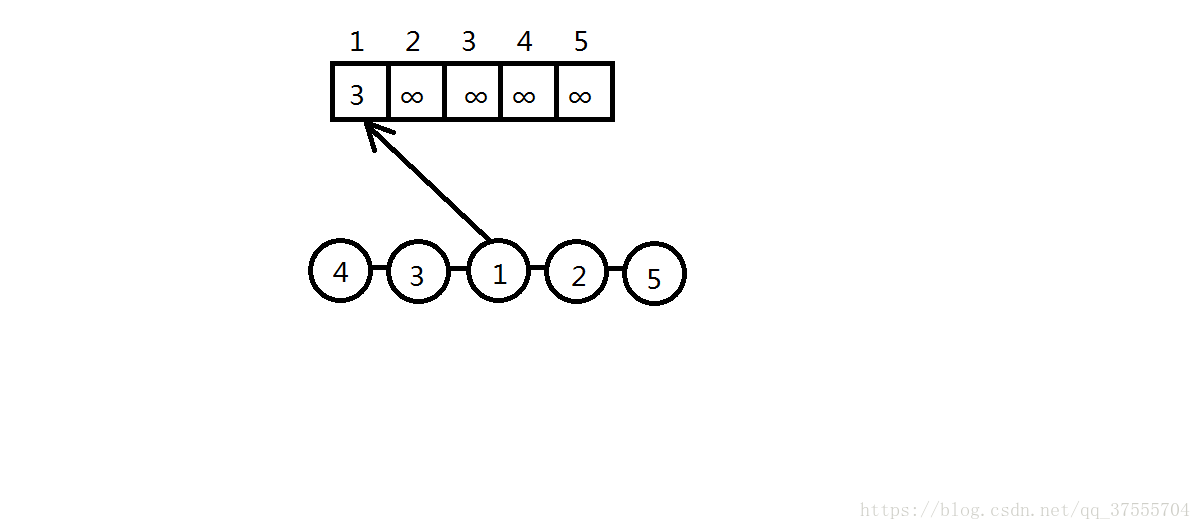
这里发现2比1大,于是更新了f[2]

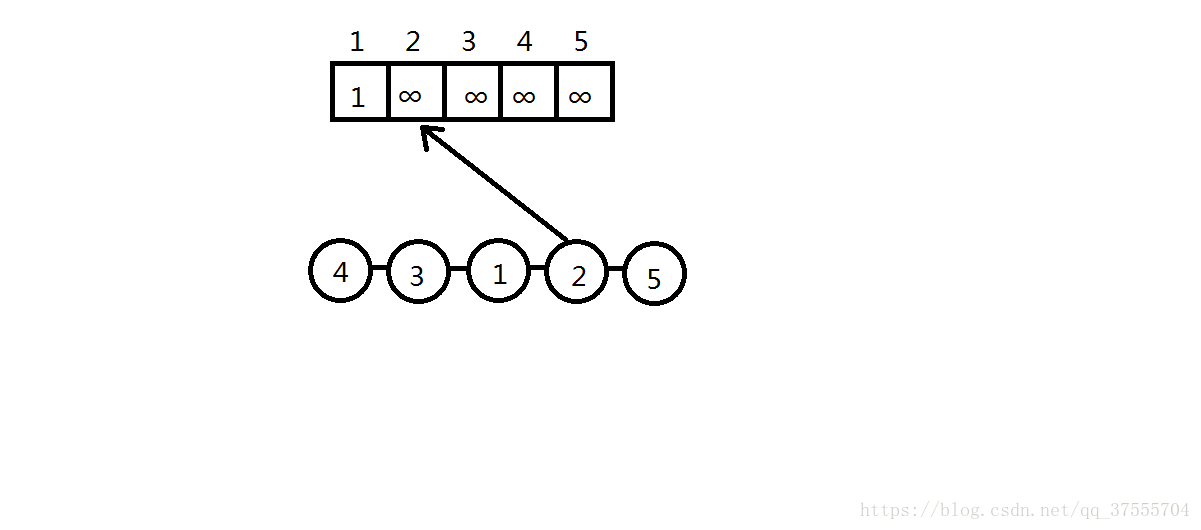
同上

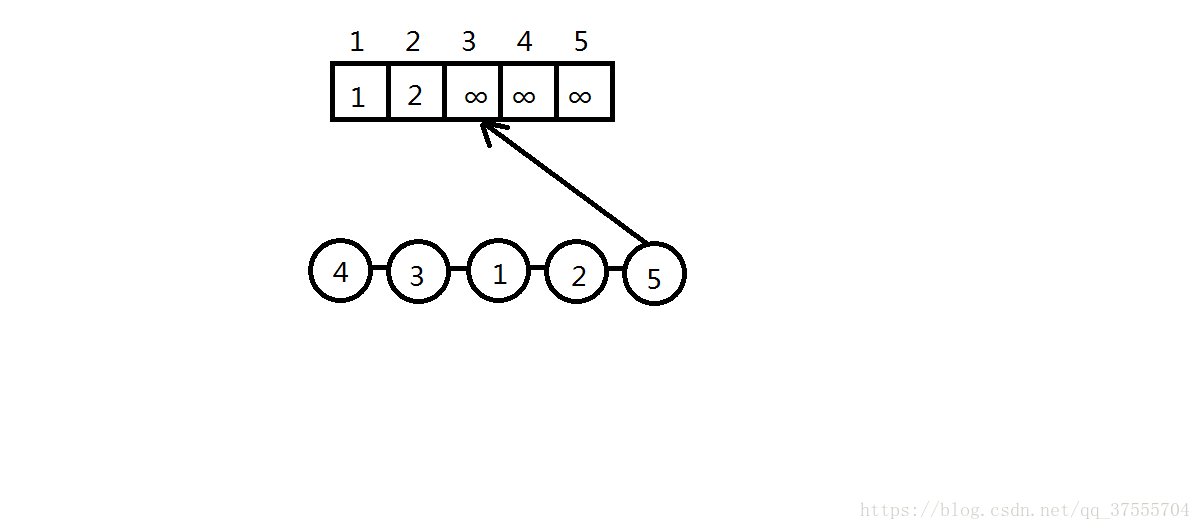
这里最后就返回了3

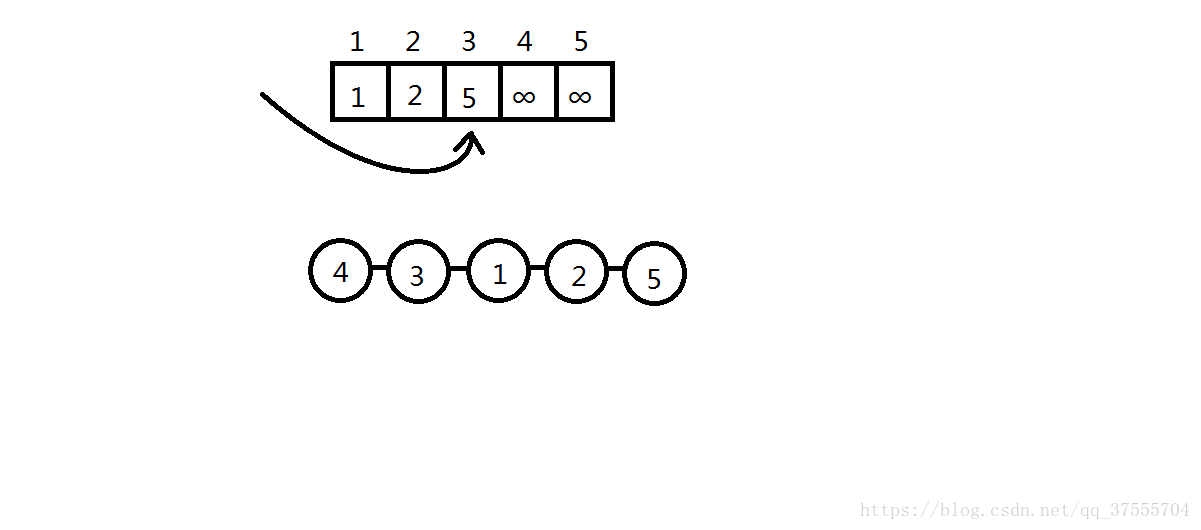
程序写起来也极为简洁.

代码

#include
#include
#include
using namespace std;
int read(){
    int f=1,x=0;char s=getchar();   
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}  
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
#define MAXN 1000
#define INF 0x3f3f3f3f
int a[MAXN+5],dp[MAXN+5];
int main(){
    int n=read();
    memset(dp,0x3f,sizeof(dp));
    for(int i=1;i<=n;i++)
        a[i]=read(),*lower_bound(dp+1,dp+n+1,a[i])=a[i];
    printf("%d\n",lower_bound(dp+1,dp+n+1,INF)-(dp+1));
    return 0;
}