不倒嗡嗡
2016年的诺贝尔奖颁发给了拓扑凝聚态物理,拓扑一时风靡全国,各种拓扑概念炙手可热。拓扑中最为常见、也是最为强有力的理论工具当同调代数莫属。神圣网格问题的基本拓扑工具既包括微分拓扑中子流形的光滑浸入理论、又包括代数拓扑中的同调理论。
一百多年以前,在庞加莱发明同调论的时候,世上没有计算机,没有有限元理论,更遑论神圣网格问题。但是同调论的核心思想恰恰正好契合了神圣网格的核心问题,其恰切程度往往令人觉得同调论的发明正是为了解决神圣网格问题。历史如此惊人的巧合,再度验证了抽象数学不可思议的普适性和实用性。今年的诺贝尔生理医学奖得主大隅良典有一句名言:“科学并不从属于技术”,另一方面,技术的发展更应该以科学为指导,顺应科学。
同调论的观点
十九世纪末叶,在美丽的法国南锡,数学家拓扑学之父庞加莱思索着这样一个问题:假如有一只具有高度智慧的蚂蚁,生活在一张曲面之上。因为蚂蚁生活的空间是二维的,它也无法跳跃,因此也没有三维概念。那么这只蚂蚁是否能够判断它生活的空间更像是一个苹果(sphere)的表面,还是一个甜甜圈(torus)的表面?对于生活在三维空间中的人类而言,这一问题显而易见,因为人类可以看到甜甜圈中间的“洞”,或称之为“环柄”,而苹果没有环柄。但是蚂蚁无法跳离曲面,因此看不到环柄。
庞加莱的问题可以如下理解:人类对照轮胎曲面和背景空间,看到了“洞”,这是否意味着轮胎(torus)曲面的环柄(洞)和轮胎在三维背景空间中的嵌入方式有关,而并非由轮胎曲面本身所内蕴决定?如果这样,那么蚂蚁只能观测到曲面的内蕴信息,因此无法判定环柄的存在。
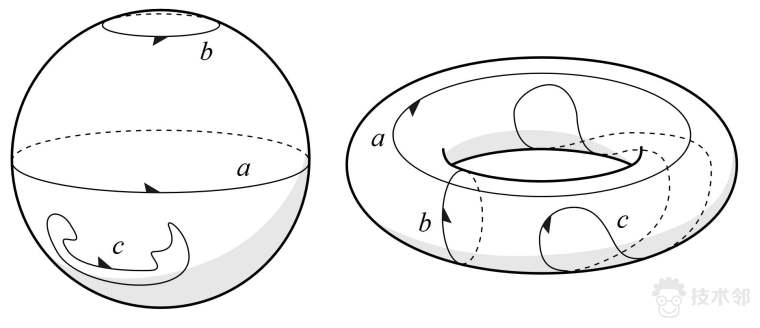
图2. 同调的基本思想:边和圈的差别。
庞加莱的想法是考察曲面上的封闭曲线,即首尾相连的“圈”。曲面上的子区域的边界我们称为“边”,所有的“边”必然是“圈”,但是有些“圈”未必是“边”。如图2所示,球面上所有的圈都围绕着子区域,换言之,球面上所有的圈都是边;但是,轮胎表面上有些圈是边,如曲线c,有些圈不是边,如曲线a和b。(如果我们沿着圈a将轮胎切开,我们会得到一个圆柱曲面,圆柱曲面的边界包含上下两个圈,因此圈a本身并不是圆柱的边界。)由此,庞加莱的解答就是令蚂蚁考察曲面上
圈和边的差别
如果封闭曲面上所有的圈都是边,那么曲面必为球面,反之,曲面上具有环柄。
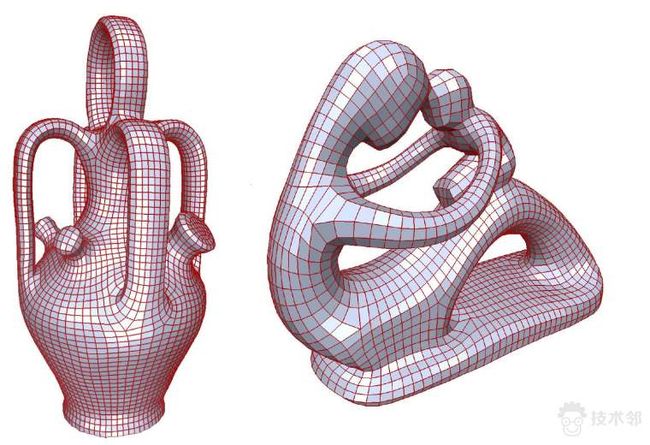
图3. 曲面的四边形网格化(Leif Kobbelt)。
六面体网格化问题
图4. 六面体网格化。
在计算机辅助工程领域(CAE),为了预测机械设计的性能,人们将机械零件剖分成六面体网格,然后用有限元方法(FEM)来求解偏微分方程。解的精确度和求解过程的效率很大程度上取决于网格化的质量。在工程实践中,人们经常将实体分解成许多零件,分别剖分每个零件,然后再整合。这就需要剖分在各个零件之间相交的界面上相互一致。一种常见的方法是先在各个零件表面上设计彼此一致的四边形网格,然后将表面的四边形网格向体内拓展成六面体网格,同时在拓展过程中保持表面四边形网格不变。这样,自然地引发了下面的问题:
在过去的二十年间,学者和工程师们坚持不懈地寻求这一问题的解答。最终,在2014年,Jeff Erickson教授用同调的语言对这个基本问题给出了最为精确、最为简洁的回答。
零调链奇偶性条件
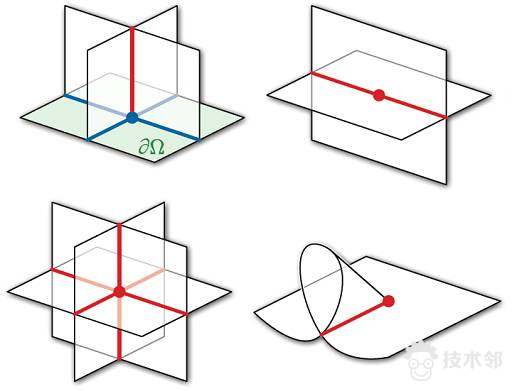
图5. 曲面光滑浸入,稳定横截相交,奇异点的分类。
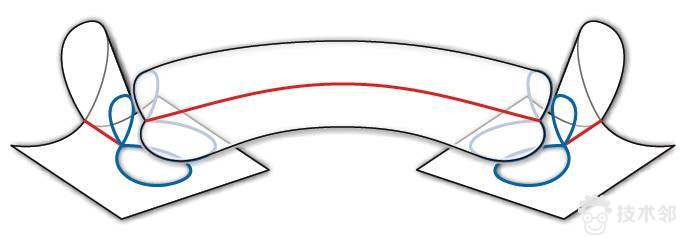
图6. 瑟斯顿的手术,消除分支奇异点【3】。
图7. 高亏格曲面上的环柄圈(handleloop, 绿色)和隧道圈(tunnelloop, 红色)。(孙剑作)
Thurston-Mitchell的理论可以被看成是Erickson理论的特例,因为球面上所有的圈都是边,四边形网格的所有2-链都由四边形组成,其边界必然有偶数条边,因此(3)自动满足,从而得出(1)和(2)也自动满足。
图8. Mitchell's 轮胎【1】。
Erickson的理论表明了一个四边形网格Q是否能够拓展成一个六面体网格H,不仅取决于Q的组合结构,同时也取决于在背景空间中的嵌入方式。如图8所示,Mitchell给出了一个轮胎的四边形网格,其在空间中有两种嵌入方式,左侧的嵌入无法拓展成六面体网格;右侧的嵌入方式却可以。
构造性证明
基于同调理论的存在性证明简洁抽象,但是并不直观,同时无法直接转换成实用的算法。Eppstein【4】给出了一种构造性方法,后来Erickson加以改进【3】。这种构造方法非常曲折,如果没有理论的存在性证明,相信Eppstein很难坚持到最后。
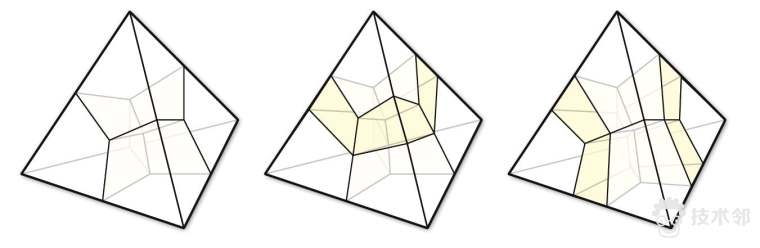
图9. 每个四面体被劈开成四个六面体。
图11. 截面增厚。
第四步:我们在Q寻找子图G,使得每个面和这个子图G有两个或者三个公共边。
小结
从以上讨论我们可以看出,四边形网格Q可拓展到六面体网格H的充分必要条件是Q的对偶是H的对偶的边缘,亦即Q的对偶是零调的。这正是同调理论的核心观点。再加上H对偶的浸入应该排除分支奇异点,由此得到了奇偶性条件。这基本概括了过去二十年间,在六面体网格生成领域的理论进展,可以用艰辛而缓慢来形容。
但是,Thurston-Mitchell-Erickson-Eppstein的理论主要关注非结构的六面体网格,在工程实践中,人们真正关注的是结构化的六面体网格。结构化六面体网格具有更加苛刻的条件,需要更为深刻的洞察和使用更加复杂的理论工具。我们在下一讲会仔细讲解。