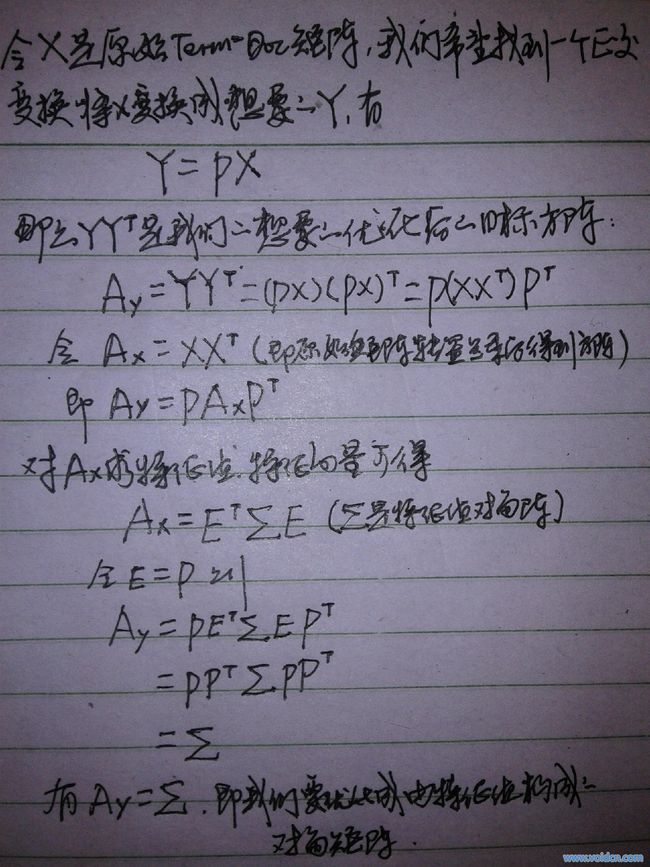一、LSA概论
1)LSA的引入
LSA(latent semantic analysis)潜在语义分析,也被称为LSI(latent semantic index),是Scott Deerwester, Susan T. Dumais等人在1990年提出来的一种新的索引和检索方法。该方法和传统向量空间模型(vector space model)一样使用向量来表示词(terms)和文档(documents),并通过向量间的关系(如夹角)来判断词及文档间的关系;而不同的 是,LSA将词和文档映射到潜在语义空间(这是个正交空间,该如何找到?下文),从而去除了原始向量空间中的一些“噪音”,提高了信息检索的精确度。
2)传统方法的缺点
传统向量空间模型使用精确的词匹配,即精确匹配用户输入的词与向量空间中存在的词。由于一词多义(polysemy)和一义多词(synonymy)的存 在,使得该模型无法提供给用户语义层面的检索。比如用户搜索”automobile”,即汽车,传统向量空间模型仅仅会返回包含”automobile” 单词的页面,而实际上包含”car”单词的页面也可能是用户所需要的。
3) LSA如何解决这些问题
LSA 潜在语义分析的目的,就是要找出词(terms)在文档和查询中真正的含义,也就是潜在语义,从而解决上节所描述的问题。具体说来就是对一个大型的文档集合使用一个合理的维度建模,并将词和文档都表示到该空间,比如有2000个文档,包含7000个索引词,LSA使用一个维度为100的向量空间将文档和词表示到该空间,进而在该空间进行信息检索。而将文档表示到此空间的过程就是SVD奇异值分解和降维的过程。降维是LSA分析中最重要的一步,通过降维,去除了文档中的“噪音”,也就是无关信息(比如词的误用或不相关的词偶尔出现在一起),语义结构逐渐呈现。相比传统向量空间,潜在语义空间的维度更小,语义关系更明确。
4)LSA的步骤
1. 分析文档集合,建立Term-Document矩阵。
2. 对Term-Document矩阵进行奇异值分解。
3. 对SVD分解后的矩阵进行降维,也就是奇异值分解一节所提到的低阶近似。
4. 使用降维后的矩阵构建潜在语义空间,或重建Term-Document矩阵。
下面是Introduction to Latent Semantic Analysis里面的一个例子,描述了完整的LSA步骤
假设文档集合如下:
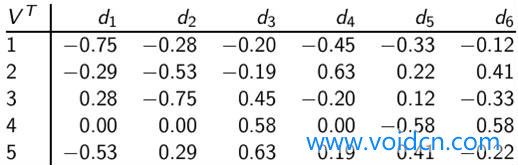
原始的Term-Document矩阵如下:
观察这个矩阵,human和user,他们没有在某篇文档中共现过,他们的关系使用Spearman coefficient来表示为
R(human,user)=-0.38,R(human,minors)=-0.29
对其进行奇异值分解:
然后对分解后的矩阵降维,这里保留{S}的最大两个奇异值,相应的{W}{P}矩阵如图,注意{P}在公式中需要转置。
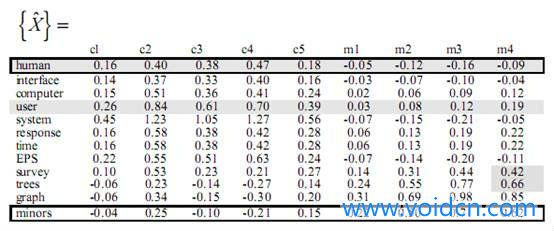
到了这一步后,我们有两种处理方法,论文Introduction to Latent Semantic Analysis是将降维后的三个矩阵再乘起来,重新构建了{X}矩阵如下:
观察这个经过奇异值分解后重新构建的矩阵,同样计算Spearman coefficient系数,R(human,user)=0.94,R(human,minors)=-0.83,可以看到human和user的相关联程度竟然达到了0.94,虽然他们在原始文档中并没有共现。
5)LSI在IR中的应用
对词项-文档矩阵进行SVD分解;
计算在新的低维空间下的文档表示;
将查询映射到新的低维空间:
由
推出(在C2左边点乘U的转置和Σ的转置),q2即表示v2
计算q2和V2中所有文档表示的相似度;
像以往一样按照相似度高低输出相似文档
二、LSA推理及说明
LSI能够发现文档的语义上的关联,但是在原始向量空间中,这些文档的相似度不大(因为他们使用不同的词语)。于是可以通过LSI将他们映射到新的低维向量空间中,在新的低维空间中,两者相似度较高。因此LSI能够解决一义多词和语义关联的问题,在标准的向量空间下,同义词对文档相似度计算没有任何贡献。
先通过一个例子,然后提出问题,解答问题。奇异值分解请参照http://hi.baidu.com/leifenglian/item/bd11affd02d4f00d84d278c8
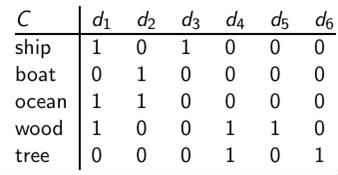
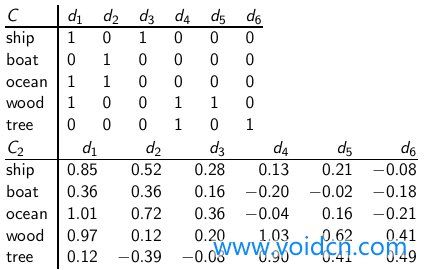
例子矩阵C:
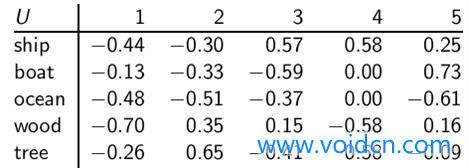
奇异值分解后矩阵U:
每个词项对应一行,每个min(M,N)对应一列,其中M为词项的数目,N是文档的数目。这是个正交矩阵:
1)列向量都是单位向量,即CC'的正交特征向量集合;
2)任意列向量之间都是相互正交的,可以想象这些列向量分别代表不同的的“语义”维度,比如政治、经济、体育等主题,元素Uij给出的是词项i和第j个语义维度之间的关系强弱程度。
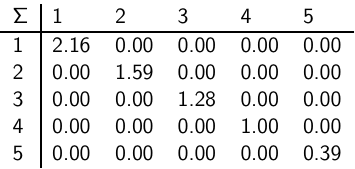
奇异值分解后矩阵Σ:
这是个min(M,N) ×min(M,N)的对角方阵。对角线上是矩阵C的奇异值,即CC'的特征值。奇异值的大小度量的是相应“语义”维度的重要性。我们可以通过忽略较小的值来忽略对应的“语义”维度。
奇异值分解后矩阵V’(转置):
每篇文章对应一列,每min(M,N)对应一行,同样也是正交矩阵:
1)每个行向量都是单位矩阵,即C'C的正交特征向量集合;2)任意两个行向量也是正交。同样每个行向量代表的是一个语义维度,矩阵元素Vij(注意没转置)代表的是文档i和语义维度j的关系强弱程度。
问题一:为什么在LSA中使用SVD分解?
1)最关键的性质:每个奇异值对应的是每个“语义”维度的权重
2)将不太重要的权重置为0,可以保留重要的信息,去掉一些信息“枝节”,这些枝节可能是噪音(简化的LSI噪音更少,是一种更好的表示方法),也有可能使本来应该相似的对象不相似,简化的LSI由于其更好的表达相似度,因而是一种更优的表示方式。
3)“细节越少越好”,把颜色去掉的花朵更容易看到两者的相似性。
只需要将矩阵Σ中的相应维度置为0即可,此时,相当于矩阵U和V的相应维度被忽略,然后重新计算出C,得到C2
C2可以看着是C的一个二维表示,ship和boat在原文档中没有共现,但在低维空间C2中语义相似
问题二:SVD的什么性质能使相似度的计算有所提高?
求CC'的特征向量集合得到了矩阵U,特征值得到了对角矩阵Σ;
求C'C的特征向量集合得到了矩阵V,CC'和C'C的特征值相同。
CC'是一个对称矩阵,矩阵元素表示的是每个词相互的共现度,从几何意义上讲,该对称矩阵表示的是一个线性变换,求该对称矩阵的特征向量集合即是寻找一组正交基来表示这个线性变换(每一个基向量可以看着是一个语义维度)。这组特征向量所表示的方向即是经矩阵变换后方向保持不变的方向而只做一定的拉伸,拉伸程度即特征值。先找到最大的一个特征值,表示在相应语义维度的重要性,即先找到一个最重要的语义维度,然后找次大的。每个语义维度之间的关联尽可能小,因为特征向量集是正交的,表示完全不同的语义方向,因此形成不同的语义空间。最后,自己的语义空间中相似度得到提高,不同语义之间的相似度得以减小以加大区分度。
几句话:
降维迫使我们忽略大量的“细节”;
我们将原始空间下不同的词映射到低维空间的同一维中;
将同义词映射到同一维的“开销”远小于无关词的聚集;
SVD选择开销最小的映射方法;
因此,SVD会将同义词映射到同一维;
但是,它同时能避免将无关词映射到同一维。
问题三:第一个做LSA的人是如何发现前K个特征值对应的特征向量可以构建出潜在的语义(词语义,主题语义)空间的?(关键!!!!)
还是看原始Term-Doc矩阵Am*n,m是特征词的个数,n是文档个数,即行向量是一个词在各个文档中的变化(可看着是一个变量的值变化情况),列向量是一篇文档中各个词的分布情况。
做LSA的过程即要求AA'的特征向量特征值,来看看AA'方阵元素表示的意义,A的行向量乘以A'的列向量,即各个词之间变化规律的一种联系,AA'对角线上的某个元素值表示每个词自身变量的变化情况,非对角线上的某个元素值表示两个词之间的共现程度(相似程度)。
AA'在向量空间中表示了一组线性变换,但是这个方阵总是不大好的,充满了噪声和冗余,我们希望找到另外一个组基来对这个方阵进行优化,以将这个方阵转变为一个空间变化意义明显的矩阵,即能体现出潜在语义空间。那么我们希望将方阵AA'优化成怎样的矩阵呢?我们希望优化成:
a)对角线上元素:拥有偏大的值。因为偏大的值表明这个词只在一部分文档中出现,且在这一类文档中占重要地位,即属于主题词,代表一类语义(以TF-IDF作为权重,如果一个词在A中所有文档中出现,那么该词的TF-IDF权重值肯定非常小,在做AA'时,权重的平方和将偏小,如果该词只在一部分文档中出现,即该词是这类文档的主题词,那么该词在这类文档中的TF-IDF权重肯定很大,在做AA'时,权重的平方和将偏大。我们即需要这样偏大的值)
b)非对角线上的元素:拥有零值。可能未优化前的方阵非对角线上元素为零值(这个最好了),也可能为很大的值(表明某个词a和某个词b存在很大的相似度,他们很可能是同一个语义,我很喜欢这个大值,因为表明找到了语义类,但注意了,他属于冗余,因为同时在相应对角线上词a(或b)也存在一个大值,我们只需要这一个大值就表示了这个语义类,多出一个都算冗余了,应该去除),也可能是一个很小的非零值(不喜欢这个很小的非零值,他可能是某个词a本"不应该"出现在某类文章中,他代表噪声,应该去除)
接下来,请看以下推导:
很明白了,我们就是要求XX'的特征值和特征向量,特征向量表示词的语义维度方向,特征值表示该维度的重要程度。这样我们就可以分解出原矩阵中所有词的语义空间。
同时,我们可求X'X,X'中的行向量表示一篇文章各个词的分布,可以把行向量看着是文档变量,不同的词组成不同的文档变量,X'X后方阵的元素表示各文档之间的相似度,对角线上的元素是文档变量自身的变化,非对角线上的元素是文档变量之间关联。我们希望优化这个A=X'X矩阵,使之优化成:
a)对角线上元素:拥有偏大的值。以TF-IDF值作为矩阵元素权重,一篇文档中,我们理想的希望有关这篇文档的所有主题词出现(主题词的TF-IDF高),所有无关的词尽量不要出现(非主题词的TF-IDF小),这样X'X后元素值的平方和达到最大,否则,由于非主题词的干扰,会使得TF-IDF元素值的平方和没有那么大。因此,使对角线上的元素拥有偏大值,即消除非主题词噪声的干扰。
b)非对角线上的元素:拥有零值。非对角线上的值可能出现很大值,此时表示两篇文档拥有很大的相似度,即表示了一个主题,次数我们只需要一个该主题的表示即可,因此他属于冗余,我们希望它为零值。也可能出现很小的非零值,此时表示两篇文档没有多少相似度,是两个无关主题,但值并不为0,这是由于两篇文档中有些词还是可能同时出现过,但此时他是噪声。我们同样希望它为零值。
因此,求X'X的特征值,特征向量,特征向量表示了某个主题维度方向,特征值表示该维度的权重。
因此,可直接对元素矩阵X进行奇异值分解,即可同时得到XX'的特征向量和X'X的特征向量,即同时得到词的语义空间和文档的主题空间!
Reference:
http://blog.csdn.net/wangran51/article/details/7408406
http://wenku.baidu.com/view/cb373a1c5f0e7cd184253634.html lecture18-lsi信息检索导论王斌
http://hi.baidu.com/leifenglian/item/abf63c11772020fe64eabf3f 主成分分析
【转】PLSA 与 LSA
细节看http://blog.csdn.net/huangxy10/article/details/8091478
1. 引子
Bag-of-Words 模型是NLP和IR领域中的一个基本假设。在这个模型中,一个文档(document)被表示为一组单词(word/term)的无序组合,而忽略了语法或者词序的部分。BOW在传统NLP领域取得了巨大的成功,在计算机视觉领域(Computer Vision)也开始崭露头角,但在实际应用过程中,它却有一些不可避免的缺陷,比如:
稀疏性(Sparseness): 对于大词典,尤其是包括了生僻字的词典,文档稀疏性不可避免;
多义词(Polysem): 一词多义在文档中是常见的现象,BOW模型只统计单词出现的次数,而忽略了他们之间的区别;
同义词(Synonym): 同样的,在不同的文档中,或者在相同的文档中,可以有多个单词表示同一个意思;
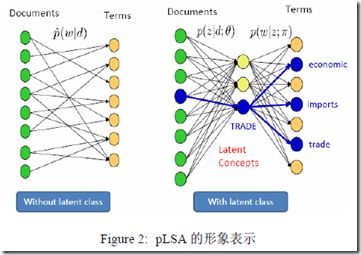
从同义词和多义词问题我们可以看到,单词也许不是文档的最基本组成元素,在单词与文档之间还有一层隐含的关系,我们称之为主题(Topic)。我们在写文章时,首先想到的是文章的主题,然后才根据主题选择合适的单词来表达自己的观点。在BOW模型中引入Topic的因素,成为了大家研究的方向,这就是我们要讲的Latent Semantic Analysis (LSA) 和 probabilitistic Latent Semantic Analysis (pLSA),至于更复杂的LDA和众多其他的Topic Models,以后再详细研究。
2. LSA简介
已知一个文档数据集
及相应的词典
,采用BOW模型假设,我们可以将数据集表示为一个
的共生矩阵,
,其中,
表示词典中的第j个单词在第i个文档中出现的次数。
LSA的基本思想就是,将document从稀疏的高维Vocabulary空间映射到一个低维的向量空间,我们称之为隐含语义空间(Latent Semantic Space).
如何得到这个低维空间呢,和PCA采用特征值分解的思想类似,作者采用了奇异值分解(Singular Value Decomposition)的方式来求解Latent Semantic Space。标准的SVD可以写为:
其中,
和
均为正交矩阵,有
,
是包含
所有奇异值的对角矩阵。LSA降维的方式就是只取
中最大的K个奇异值,而其他置为0,得到
的近似矩阵
,于是得到了共生矩阵的近似:
注意到如果我们利用内积来计算文档与文档之间的的相似度,即
的自相关矩阵,可以得到:
。于是,我们可以把
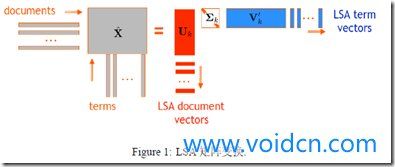
解释为文档样本在Latent Space上的坐标,而
则是两个空间之间的变换矩阵。下图形象的展示了LSA的过程:
由LSA在训练集合上得到的参数,当一个新的文档向量
到来时,我们可以利用下式将其原始term space映射到latent space:
LSA的优点
低维空间表示可以刻画同义词,同义词会对应着相同或相似的主题;
降维可去除部分噪声,是特征更鲁棒;
充分利用冗余数据;
无监督/完全自动化;
与语言无关;
LSA的不足
没有刻画term出现次数的概率模型;
无法解决多义词的问题;
SVD的优化目标基于L-2 norm 或者是 Frobenius Norm的,这相当于隐含了对数据的高斯噪声假设。而term出现的次数是非负的,这明显不符合Gaussian假设,而更接近Multi-nomial分布;
对于count vectors 而言,欧式距离表达是不合适的(重建时会产生负数);
特征向量的方向没有对应的物理解释;
SVD的计算复杂度很高,而且当有新的文档来到时,若要更新模型需重新训练;
维数的选择是ad-hoc的;
3. pLSA
类似于LSA的思想,在pLSA中也引入了一个Latent class,但这次要用概率模型的方式来表达LSA的问题,如下图:
在这个probabilitistic模型中,我们引入一个Latent variable
,这对应着一个潜在的语义层。于是,完整的模型为:
代表文档在数据集中出现的概率;
代表当确定了语义
时,相关的term(word)出现的机会分别是多少;
表示一个文档中语义分布的情况。利用以上这些定义,我们就可以一个生成式模型(generative model),利用它产生新的数据:
首先根据分布
随机抽样选择一个文档
;
选定文档后,根据
抽样选择文档表达的语义
;
选定语义后,根据
选择文档的用词;
这样,我们得到了一个观测对
,多次重复这一过程我们就得到了一个类似N的共生矩阵,而潜在的语义
在观测值中并没有表现出来。为了刻画
的联合分布,我们可得到以下公式:
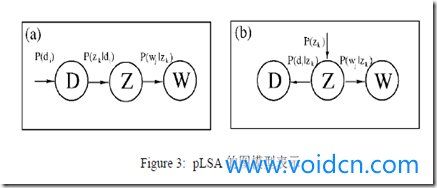
用图模型来表示以上公式如Figure3中的(a),而(b)是pLSA模型的另外一种等价形式,公式可写作:
模型确定好了,已知的数据集N,我们可以利用Maximum Likelihood准则来确定模型的参数,目标函数可写作:
此目标函数也可以解释为使
与
两个分布之间的K-L Divergence最小,即
更好的刻画共生矩阵的实际分布。
EM求解
在似然值
的表达式中存在对数内部的加运算,所以球pLSA最大似然解的问题没有闭式解,我们只能求助于EM算法,下面我们从最简单的启发式的角度推导出pLSA的求解过程。
既然似然值
无法直接求解最大值,那么我们转而优化其下界
,并通过迭代不断的将此下界提高,那么最终得到的解即为
近似最大解, 当然,此过程中寻求的下界
要求尽量紧确。利用琴生不等式和概率小于1的性质,我们可以得到如下推导:
这样,我们就把
拿到了
外面来,接下来我们就可以对
直接求解了。注意这个最大化问题的约束条件是:
利用拉格朗日法,我们可以得到优化目标:
对此目标函数求导,我们可以得到EM算法中的M-step:
而EM算法中的E-step也就是求已知
时隐含变量
的后验概率:
观察可以得到,E-step与M-step互相依赖,可以证明每一步都使得下界
的期望值提高,通过不断的迭代求解即可最后求得原问题的近似最大似然解。
pLSA与LSA的关系
由Figure4可以看到pLSA与LSA之间的对应关系。其中
刻画了Latent Space也即topic space的信息;
刻画了topic space与term space之间的关系,对应着LSA中的正交基
;在文档分类是,这两部分也就是我们在模型训练结束需要保存的信息,当一个新的文档的到来时, 我们可以再次利用EM算法得到新的文档与主题的对应关系
,并由此得到文档在topic空间上的表示
。
pLSA的优势
定义了概率模型,而且每个变量以及相应的概率分布和条件概率分布都有明确的物理解释;
相比于LSA隐含了高斯分布假设,pLSA隐含的Multi-nomial分布假设更符合文本特性;
pLSA的优化目标是是KL-divergence最小,而不是依赖于最小均方误差等准则;
可以利用各种model selection和complexity control准则来确定topic的维数;
pLSA的不足
概率模型不够完备:在document层面上没有提供合适的概率模型,使得pLSA并不是完备的生成式模型,而必须在确定document i的情况下才能对模型进行随机抽样;
随着document和term 个数的增加,pLSA模型也线性增加,变得越来越庞大;
当一个新的document来到时,没有一个好的方式得到$p(d_i)$;
EM算法需要反复的迭代,需要很大计算量;
针对pLSA的不足,研究者们又提出了各种各样的topic based model, 其中包括大名鼎鼎的Latent Dirichlet Allocation (LDA),在此就不再多说了。
4. 参考文献
Thomas Hofmann, “Unsupervised Learning by Probabilistic Latent Semantic Analysis,” Machine Learning 42, no. 1 (January 1, 2001): 177-196.
转自http://tech.bobgo.net/?p=135
什么是LDA?
主题模型LDA(latent dirichlet allocation)的应用还是很广泛的,之前我自己在检索、图像分类、文本分类、用户评论的主题词抽取等都用过,做feature、降维等。例如可以用主题维度来表示原来的字典维度,大大的降低了文本表示的维度。这其实也很deep
learning中的对特征的抽象有点相似,通过一些聚类等的思想,将一些细粒度的特征组合到一个新的空间上去,例如主题空间。