前言
本来是内部做分享交流Core Text，懒得做PPT，坐标系转换这块单独写篇文章倒省事
正文
上篇文章从零到一撸个YYLabel中提到过
Core Text是Apple的文字渲染引擎，坐标系为自然坐标系，即左下角为坐标原点，而iOS坐标原点在左上角。所以，在iOS上用Core Text绘制文字时，需要转换坐标系
通常情况下，坐标系转换会这么写
CGContextTranslateCTM(context, 0, size.height);
CGContextScaleCTM(context, 1, -1);
所谓知其然，知其所以然。为啥这样写就可以转换坐标系？这要从CGAffineTransform说起
CGAffineTransform
CGAffineTransform是用于绘制二维图形的仿射变换矩阵，用结构体定义
typedef struct CGAffineTransform CGAffineTransform;
struct CGAffineTransform {
CGFloat a, b, c, d;
CGFloat tx, ty;
};
CGAffineTransform对应一个3*3矩阵，可以看到矩阵中9个元素最后一列总是001，其余6个元素与CGAffineTransform结构体各成员一一对应。搞过Core Animation的都知道，还有个东西叫做CATransform3D，那是个更繁琐的矩阵，超出本文范围，这里不做赘述。
回顾一下线性代数的基本知识：任意矩阵乘以单位矩阵等于原矩阵（AE = A）
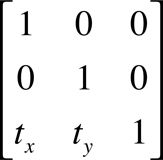
所谓单位矩阵，即主对角线（左上到右下的对角线）元素为1，其余元素为0的m*m矩阵，如下图3*3单位矩阵
先看这几个基本函数：
CGAffineTransform CGAffineTransformMake(CGFloat a, CGFloat b, CGFloat c, CGFloat d, CGFloat tx, CGFloat ty);
CGAffineTransform CGAffineTransformMakeTranslation(CGFloat tx, CGFloat ty);
CGAffineTransform CGAffineTransformMakeScale(CGFloat sx, CGFloat sy);
CGAffineTransform CGAffineTransformMakeRotation(CGFloat angle);
-
CGAffineTransformMake
CGAffineTransformMake最简单，用于生成一个各元素对应的3*3矩阵
CGAffineTransformMake.png
-
CGAffineTransformMakeTranslation
CGAffineTransformMakeTranslation用来移动坐标，tx对应X轴移动单位，ty对应Y轴移动单位，生成矩阵为
CGAffineTransformMakeTranslation.png
可以看到，当tx = ty = 0时，就是单位矩阵，所以CGAffineTransformMakeTranslation生成的矩阵只会影响X轴与Y轴。如果有坐标(x, y)，那么新坐标是如何得到的？
很简单，只要将(x, y)坐标点转换成1*3矩阵即可：[x y 1]。
用坐标矩阵乘以CGAffineTransformMakeTranslation生成矩阵即可得到新矩阵[x+tx y+ty 1]，对应坐标方程为：
-
CGAffineTransformMakeScale
CGAffineTransformMakeScale用来缩放坐标，sx对应X轴缩放系数，sy对应Y轴缩放系数，生成矩阵为：
CGAffineTransformMakeScale.png
同理，当sx = sy = 1时，就是单位矩阵。用坐标矩阵[x y 1]乘以CGAffineTransformMakeScale生成矩阵可得新矩阵[x*sx y*sy 1]，对应方程为：
- CGAffineTransformMakeRotation
CGAffineTransformMakeRotation用来旋转坐标，α对应坐标系旋转角度，生成矩阵为：
当α = 0时，cos α = 1， ±sin α = 0。同样，这是一个单位矩阵。 用坐标矩阵乘以CGAffineTransformMakeRotation生成矩阵可以得到新矩阵[(x*cosα-y*sinα) (x*sinα+y*cosα) 1]，对应方程为：
平移和缩放得到的方程直接看得出是对的，来简单验证下旋转方程的正确性：
在自然坐标系中（原点为左下角的坐标系），假设原坐标点A(3, 3)，求点A逆时针旋转90度后新坐标点A'。（逆时针旋转90度，即：α = -π/2）
带入上述公式后可得A'(-3, 3)，显然正确
这里又得说到坐标原点的事了，iOS坐标原点为左上角，macOS坐标原点为左下角，所以：
- 在iOS坐标系中
α > 0，逆时针旋转
α < 0，顺时针旋转
macOS坐标系中刚好相反
- 在macOS坐标系中
α > 0，顺时针旋转
α < 0，逆时针旋转
OK，有了这些知识储备，再来看这两句代码为啥可以翻转坐标系
// void CGContextTranslateCTM(CGContextRef cg_nullable c, CGFloat tx, CGFloat ty);
// void CGContextScaleCTM(CGContextRef cg_nullable c, CGFloat sx, CGFloat sy);
CGContextTranslateCTM(context, 0, size.height);
CGContextScaleCTM(context, 1, -1);
CGContextTranslateCTM X轴移动tx个单位，Y轴移动ty个单位是如何做到的？其实就是通过CGAffineTransformMakeTranslation对原坐标系进行矩阵变换。CGContextScaleCTM X轴缩放sx倍，Y轴缩放sy倍也是通过CGAffineTransformMakeScale对原坐标系进行矩阵变换
所以，这两句代码可以翻转坐标系
同理，CGContextRotateCTM 坐标系旋转α角度，是通过CGAffineTransformMakeRotation对原坐标系进行矩阵变换
Happy Ending！