上次给大家分享了《2017年最全的excel函数大全12—工程函数(下)》,这次分享给大家兼容性函数(上),如果你使用的是 Excel 2007,则可以在“公式”选项卡上的统计或数学与三角函数类别中找到这些函数。
BETADIST 函数
描述
返回累积 beta 概率密度函数。 Beta 分布通常用于研究样本中一定部分的变化情况,例如,人们一天中看电视的时间比率。
有关新函数的详细信息,请参考 BETA.DIST 函数。
用法
BETADIST(x,alpha,beta,[A],[B])
BETADIST 函数用法具有以下参数:
X 必需。 用来计算其函数的值,介于值 A 和 B 之间。
Alpha 必需。 分布参数。
Beta 必需。 分布参数。
A 可选。 x 所属区间的下界。
B 可选。 x 所属区间的上界。
备注
如果任何一个参数是非数值型,则 BETADIST 返回 #VALUE! 错误值。
如果 alpha ≤ 0 或 beta ≤ 0,则 BETADIST 返回 #NUM! 错误值。
如果 x < A、x > B 或 A = B,则 BETADIST 返回 #NUM! 错误值。
如果省略 A 或 B 值,则 BETADIST 使用标准的累积 beta 分布,即 A = 0,B = 1。
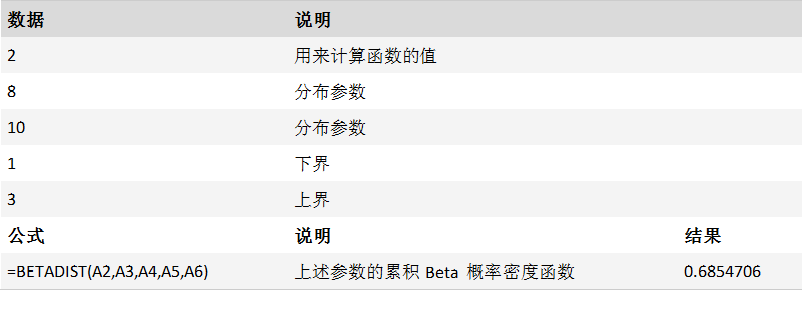
案例
描述
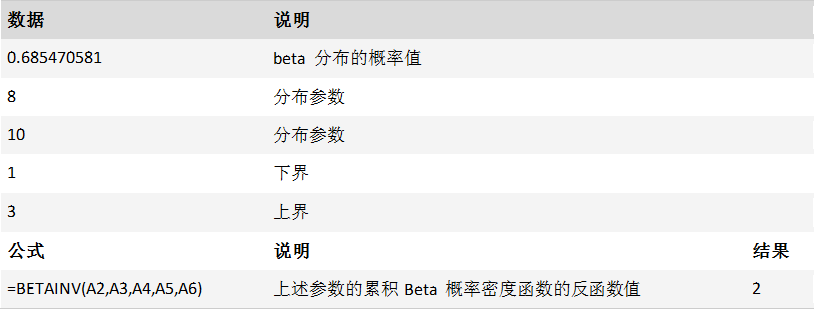
返回指定 beta 分布的累积 beta 概率密度函数的反函数。 也就是说,如果 probability = BETADIST(x,...),则 BETAINV(probability,...) = x。 beta 分布函数可用于项目设计,在已知预期的完成时间和变化参数后,模拟可能的完成时间。
有关新函数的详细信息,请参考 BETA.INV 函数。
用法
BETAINV(probability,alpha,beta,[A],[B])
BETAINV 函数用法具有以下参数:
Probability 必需。 与 beta 分布相关的概率。
Alpha 必需。 分布参数。
Beta 必需。 分布参数。
A 可选。 x 所属区间的下界。
B 可选。 x 所属区间的上界。
备注
如果任何一个参数是非数值型,则 BETAINV 返回 #VALUE! 错误值。
如果 alpha ≤ 0 或 beta ≤ 0,则 BETAINV 返回 #NUM! 错误值。
如果 probability ≤ 0 或 probability > 1,则 BETAINV 返回 #NUM! 错误值。
如果省略 A 或 B 值,则 BETAINV 使用标准的累积 beta 分布,即 A = 0,B = 1。
如果已给定概率值,则 BETAINV 使用 BETADIST(x, alpha, beta, A, B) = probability 求解数值 x。 因此,BETAINV 的精度取决于 BETADIST 的精度。
案例
BINOMDIST 函数
描述
返回一元二项式分布的概率。 BINOMDIST 用于处理固定次数的试验或实验问题,前提是任意试验的结果仅为成功或失败两种情况,实验是独立实验,且在整个试验过程中成功的概率固定不变。 例如,BINOMDIST 可以计算三个即将出生的婴儿中两个是男孩的概率。
有关新函数的详细信息,请参考 BINOM.DIST 函数。
用法
BINOMDIST(number_s,trials,probability_s,cumulative)
BINOMDIST 函数用法具有以下参数:
Number_s 必需。 试验的成功次数。
Trials 必需。 独立试验次数。
Probability_s 必需。 每次试验成功的概率。
Cumulative 必需。 决定函数形式的逻辑值。 如果 cumulative 为 TRUE,则 BINOMDIST 返回累积分布函数,即最多存在 number_s 次成功的概率;如果为 FALSE,则返回概率密度函数,即存在 number_s 次成功的概率。
备注
Number_s 和 trials 将被截尾取整。
如果 number_s、trials 或 probability_s 是非数值型,则 BINOMDIST 返回 #VALUE! 错误值。
如果 number_s < 0 或 number_s > trials,则 BINOMDIST 返回 #NUM! 错误值。
如果 probability_s < 0 或 probability_s > 1,则 BINOMDIST 返回 #NUM! 错误值。
如果 x = number_s、n = trials 且 p = probability_s,则二项概率质量函数为:
其中:
![]()
等于 COMBIN(n,x)。
如果 x = number_s、n = trials 且 p = probability_s,则累积二项分布为:
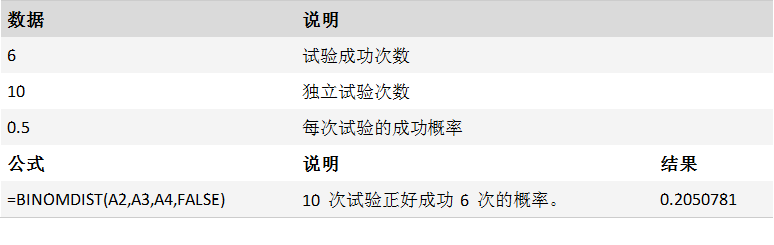
案例
CHIDIST 函数
描述
返回 χ2 分布的右尾概率。 χ2 分布与 χ2 测试相关联。 使用 χ2 测试可比较观察值和预期值。 例如,某项遗传学实验可能假设下一代植物将呈现出某一组颜色。 通过使用该函数比较观察结果和理论值,可以确定初始假设是否有效。
有关新函数的详细信息,请参考 CHISQ.DIST 函数和CHISQ.DIST.RT 函数。
用法
CHIDIST(x,deg_freedom)
CHIDIST 函数用法具有以下参数:
X 必需。 用来计算分布的数值。
Deg_freedom 必需。 自由度数。
备注
如果任何一个参数是非数值型,则 CHIDIST 返回 #VALUE! 错误值。
如果 x 为负值,CHIDIST 返回 #NUM! 错误值。
如果 deg_freedom 不是整数,则将被截尾取整。
如果 deg_freedom < 1 或 deg_freedom > 10^10,则 CHIDIST 返回 #NUM! 错误值。
CHIDIST 的计算公式为 CHIDIST = P(X>x),其中 X 为 χ2 随机变量。
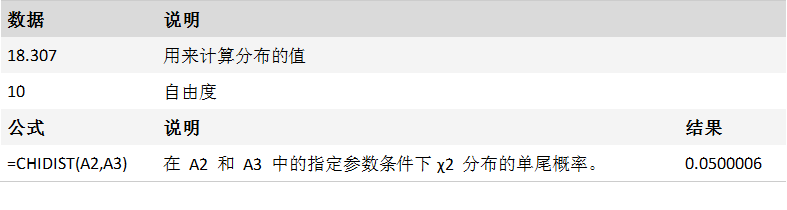
案例
CHIINV 函数
描述
返回 χ2 分布的右尾概率的反函数。 如果 probability = CHIDIST(x,...),则 CHIINV(probability,...) = x。 使用此函数可比较观察结果与理论值,以确定初始假设是否有效。
有关新函数的详细信息,请参考CHISQ.INV 函数和 CHISQ.INV.RT 函数。
用法
CHIINV(probability,deg_freedom)
CHIINV 函数用法具有以下参数:
Probability 必需。 与 χ2 分布相关联的概率。
Deg_freedom 必需。 自由度数。
说明
如果任何一个参数是非数值型,则 CHIINV 返回 #VALUE! 错误值。
如果 probability < 0 或 probability > 1,则 CHIINV 返回 #NUM! 错误值。
如果 deg_freedom 不是整数,则将被截尾取整。
如果 deg_freedom < 1,则 CHIINV 返回 #NUM! 错误值。
如果已给定概率值,则 CHIINV 使用 CHIDIST(x, deg_freedom) = probability 求解数值 x。 因此,CHIINV 的精度取决于 CHIDIST 的精度。 CHIINV 使用迭代搜索技术。 如果搜索在 100 次迭代之后没有收敛,则函数返回错误值 #N/A。
案例
CHITEST 函数
描述
返回独立性检验值。 CHITEST 返回卡方 (χ2) 分布的统计值和相应的自由度数。 您可以使用 χ2 检验值确定假设结果是否经过实验验证。
有关新函数的详细信息,请参考 CHISQ.TEST 函数。
用法
CHITEST(actual_range,expected_range)
CHITEST 函数用法具有以下参数:
Actual_range 必需。 包含观察值的数据区域,用于检验预期值。
Expected_range 必需。 包含行列汇总的乘积与总计值之比率的数据区域。
备注
如果 actual_range 和 expected_range 数据点的个数不同,则函数 CHITEST 返回错误值 #N/A。
χ2 检验首先使用下面的公式计算 χ2 统计:
其中:
Aij = 第 i 行、第 j 列的实际频率
Eij = 第 i 行、第 j 列的预期频率
r = 行数
c = 列数
χ2 低值是独立性的指示器。 从公式中可看出,χ2 始终为正数或 0,且仅当每个 i,j 的 Aij = Eij 时为 0。
CHITEST 返回在独立的假设条件下,χ2 统计的值偶然发生与以上公式计算出的值至少一样高的概率。 在计算此概率时,CHITEST 将 χ2 分布与相应自由度 (df) 一起使用。 如果 r > 1 且 c > 1,则 df = (r - 1)(c - 1)。 如果 r = 1 且 c > 1,则 df = c - 1,或者如果 r > 1 且 c = 1,则 df = r - 1。 不允许 r = c= 1,将返回 #N/A。
当 Eij 不会太小时,最适合使用 CHITEST。 某些统计人员建议每个 Eij 应该大于或等于 5。
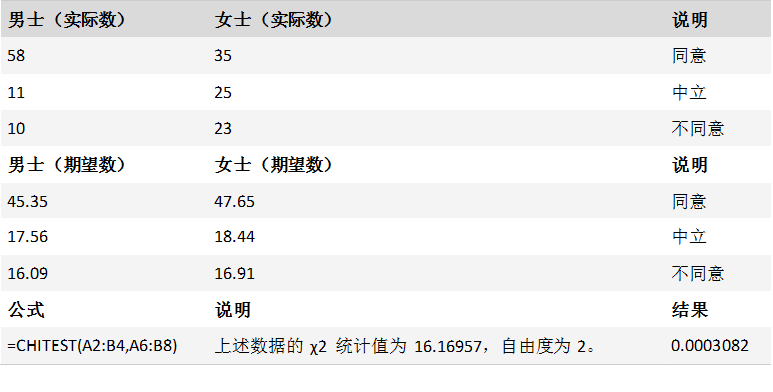
案例
CONCATENATE 函数
描述
使用 CONCATENATE(其中一个文本函数)将两个或多个文本字符串联接为一个字符串。
用法
CONCATENATE(text1, [text2], ...)
例如:
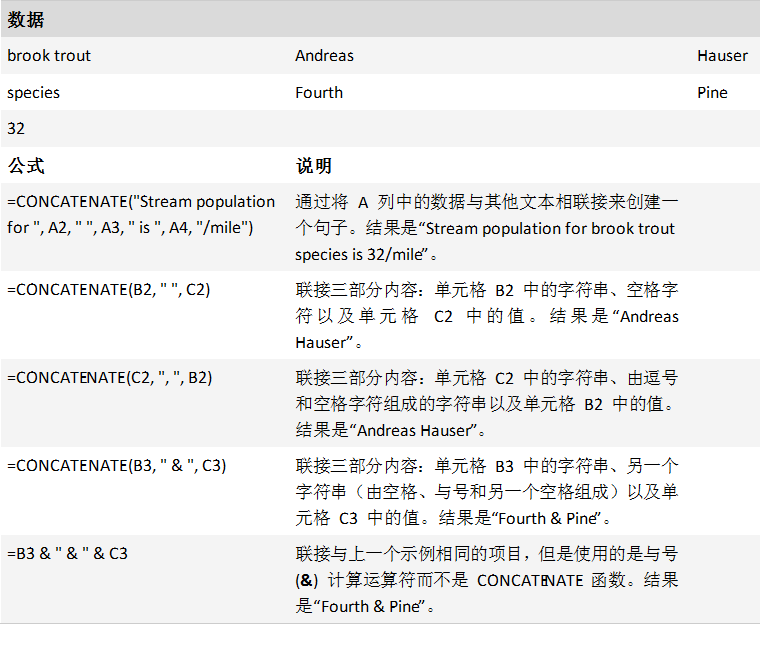
=CONCATENATE("Stream population for ", A2, " ", A3, " is ", A4, "/mile")
=CONCATENATE(B2, " ", C2)
案例
最佳做法
CONFIDENCE 函数
说明
使用正态分布返回总体平均值的置信区间。
置信区间为某一范围的值。 样本平均值 x 位于此范围的中心,此范围为 x ± CONFIDENCE。 例如,如果 x 是通过邮件订购的产品交付时间的样本平均值,x ± CONFIDENCE 为总体平均值范围。 对于在此范围中的任意总体平均值 μ0,从 μ0 而非 x 中获取样本平均值的概率大于 alpha;对于不在此范围内的任意总体平均值 μ0,从 μ0 而非 x 中获取样本平均值的概率小于 alpha。 换言之,假设我们使用 x、standard_dev 和字号在显著性水平 alpha 上构建一个双尾测试,其中假设总体平均值为 μ0。 则如果 μ0 处于置信区间,我们将不会拒绝该假设;如果 μ0 未处于置信区间,则将拒绝该假设。 置信区间无法使我们推断出概率 1 - alpha,即我们的下一个包的发送时间处于置信区间内。
有关新函数的详细信息,请参考 CONFIDENCE.NORM 函数和 CONFIDENCE.T 函数。
用法
CONFIDENCE(alpha,standard_dev,size)
CONFIDENCE 函数用法具有下列参数:
Alpha 必需。 用来计算置信水平的显著性水平。 置信水平等于 100*(1 - alpha)%,亦即,如果 alpha 为 0.05,则置信水平为 95%。
standard_dev 必需。 数据区域的总体标准偏差,假定为已知。
大小 必需。 样本大小。
备注
如果任一参数为非数值,则 CONFIDENCE 返回 #VALUE! 错误值 #REF!。
如果 Alpha ≤ 0 或 ≥ 1,则 CONFIDENCE 返回 #NUM! 错误值 #REF!。
如果 standard_dev ≤ 0,则 CONFIDENCE 返回 #NUM! 错误值 #REF!。
如果 Size 不是整数,将被截尾取整。
如果 Size < 1,则 CONFIDENCE 返回 #NUM! 错误值 #REF!。
如果假设 Alpha 等于 0.05,则需要计算等于 (1 - alpha) 或 95% 的标准正态分布曲线之下的面积。 其面积值为 ±1.96。 因此置信区间为:
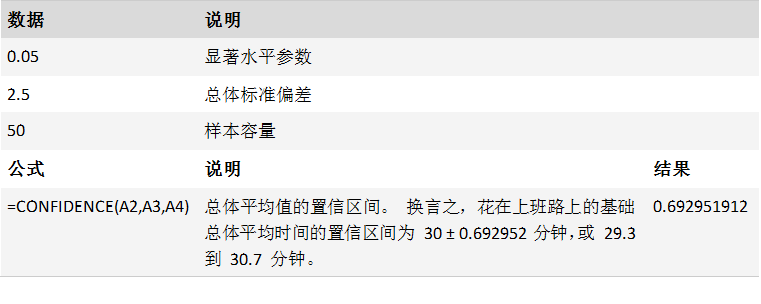
案例
COVAR 函数
描述
返回协方差,即两个数据集中每对数据点的偏差乘积的平均数。
利用协方差确定两个数据集之间的关系。例如,您可检查教育程度与收入是否成正比。
有关新函数的详细信息,请参考 COVARIANCE.P 函数和 COVARIANCE.S 函数。
用法
COVAR(array1,array2)
COVAR 函数用法具有下列参数:
Array1 必需。整数的第一个单元格区域。
Array2 必需。整数的第二个单元格区域。
备注
参数必须是数字,或者是包含数字的名称、数组或引用。
如果数组或引用参数包含文本、逻辑值或空白单元格,则这些值将被忽略;但包含零值的单元格将计算在内。
如果 array1 和 array2 所含数据点的个数不等,则函数 COVAR 返回错误值 #N/A。
如果 array1 和 array2 当中有一个为空,则函数 COVAR 返回错误值 错误值 #NUM!。
协方差计算公式为
其中
![]()
是样本平均值 AVERAGE(array1) 和 AVERAGE(array2),n 是样本大小。
案例
CRITBINOM 函数
描述
返回一个数值,它是使得累积二项式分布的函数值大于等于临界值的最小整数。 此函数可用于质量检验。 例如,使用 CRITBINOM 来决定装配线上整批产品达到检验合格所允许的最多残次品个数。
有关新函数的详细信息,请参考 BINOM.INV 函数。
用法
CRITBINOM(trials,probability_s,alpha)
CRITBINOM 函数用法具有下列参数:
Trials 必需。 贝努利试验次数。
Probability_s 必需。 一次试验中成功的概率。
Alpha 必需。 临界值。
备注
如果任一参数为非数值型,则 CRITBINOM 返回错误值 #VALUE!。
如果 trials 不是整数,将被截尾取整。
如果 trials < 0,则 CRITBINOM 返回 错误值 #NUM!。
如果 probability_s < 0 或 probability_s > 1,则 CRITBINOM 返回 错误值 #NUM!。
如果 alpha < 0 或 alpha > 1,则 CRITBINOM 返回 错误值 #NUM!。
案例
 以上是所有EXCEL的兼容性函数(上)描述用法以及使用案例。这次分享中存在哪些疑问或者哪些不足,可以在下面进行评论。如果觉得不错,可以分享给你的朋友,让大家一起掌握这些excel的兼容性函数(上)。
以上是所有EXCEL的兼容性函数(上)描述用法以及使用案例。这次分享中存在哪些疑问或者哪些不足,可以在下面进行评论。如果觉得不错,可以分享给你的朋友,让大家一起掌握这些excel的兼容性函数(上)。