1.栈的应用:
1.1浏览器前进与后退
1. 顺序查看了a->b->c三个页面,将a->b->c压入栈X
2. 点击后退按钮,从c->b->a 将 c, b 放入栈Y中
3. 点击前进按钮, 将 b 放入到栈X中
4. b 跳转新到新页面 d ,则需要清空栈Y
1.2括号匹配
检测表达式: 4+(2+8)*[5/(9-7)] 括号是否匹配
思路: 依次读入字符,如果是左括号,将它放进栈,如果是右括号,而且栈顶元素是相对应的左括号,就把栈顶元素弹出,最后如果栈空就跳出循环,结果为no,因为这样说明栈中没有左括号;字符全都读入,如果栈空的话,就是yes,否则就是no。
1. 检测到第一个括号“(”,进栈;
2. 检测到第二个括号“)”,进栈。子表达式 “4+(2+8)” 完成匹配,匹配的括号都出栈;
3. 检测到第三个括号“[”,进栈;
4. 检测到第四个括号“(”,进栈。与(3)中的括号不匹配,但由于同是左括号,可以继续匹配;
5. 检测到第五个括号“)”,进栈。由括号的作用可知,后来的括号比先来的括号优先级高,因此与(4)中括号匹配,匹配的括号都出栈;
6. 检测到第六个括号“]”,进栈。由于原来优先级更高的括号已完成,因此与(3)中括号匹配。匹配的括号都出栈,至此所有括号匹配完成。
1.3表达式求值
计算表达式: 6* (2 + 3 )*8 + 5
思路:
使用两个栈,stack0用于存储操作数,stack1用于存储操作符
从左往右扫描,遇到操作数入栈stack0
遇到操作符时,如果优先级低于或等于栈顶操作符优先级,则从stack0弹出两个元素进行计算,并压入stack0,继续与栈顶操作符的比较优先级
如果遇到操作符高于栈顶操作符优先级,则直接入栈stack1
遇到左括号,直接入栈stack1,遇到右括号,则直接出栈并计算,直到遇到左括号
1. 以表达式 6* ( 2 + 3 )*8 + 5 为例,从左向又扫描字符, 6 和 * 分别入栈
2. 继续往后扫描,遇到 ( 直接入栈,2 入栈,栈顶是左括号,+ 入栈,3 入栈
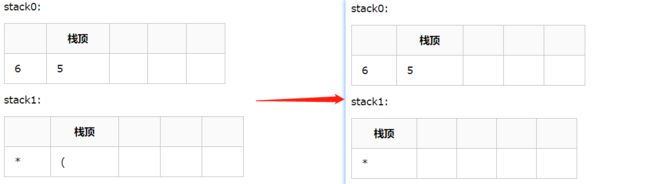
3. 向后扫描,遇到 ),它与栈顶操作符 + 相比,优先级要高,因此将 + 出栈,弹出两个操作数3 和2 ,计算结果得到 5 ,并入栈
4. 继续出栈,直到遇到左括号
5. 继续扫描,* 入栈, 与stack1栈顶 * 优先级相等, 弹出 5和 6 计算结果为30, 后面 8 入栈,+ 优先级小于 * ,弹出操作数计算得到结果240,并将其入栈,最后 + 也入栈
6. 最后 5 入栈,发现操作符栈不为空,弹出操作符 + 和两个操作数,并进行计算,得到 245 ,入栈,得到最终结果。
2. 如何快读找到一个链表的中间结点
链表与数组最大的区别之一就是 链表内存空间不连续,不可以随机访问。
数组相比链表的优劣:数组连续空间更利于CPU缓存;链表可充分利用内存碎片
思路:快慢指针遍历法。A指针每次移动一个节点,B指针每次移动两个节点。当B到达end的时候,A的位置即为中点
普通方法: 循环单链表,确定单链表的长度,然后循环长度1/2确定中间节点.
缺点: 需要遍历 L+L/2 次 ,算法难度 O(L+L/2)=O(3L/2)
快慢指针遍历法: 需要遍历L/2 次, 算法复杂度O(L/2)
3. LRU算法如何用链表实现?
LRU(Least recently used,最近最少使用)
LRU算法根据数据的历史访问记录来进行淘汰数据,其核心思想是“如果数据最近被访问过,那么将来被访问的几率也更高”。
解法:
1. 有序链表,按照访问时间倒序,头部时间戳>尾部时间戳
2. 元素A被访问,遍历链表,如果此数据在原链表中,将其从原来位置删除,然后插入到头部
3. 如果A不在原链表中,则判断链表是否已满;如果未满,插入到头部;如果已满,删除一个尾部元素,然后将A插入到头部
【命中率】 当存在热点数据时,LRU的效率很好,但偶发性的、周期性的批量操作会导致LRU命中率急剧下降,缓存污染情况比较严重。
【复杂度】 实现简单。
【代价】 命中时需要遍历链表,找到命中的数据块索引,然后需要将数据移到头部。如果Cache的数量少,问题不会很大, 但是如果Cache的空间过大,达到10W或者100W以上,一旦需要淘汰,则需要遍历所有计算器,其性能与资源消耗是巨大的。效率也就非常的慢了。