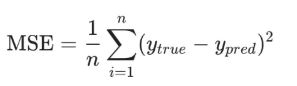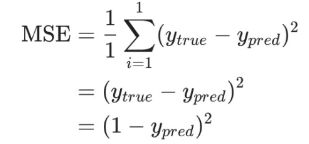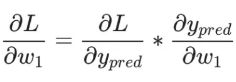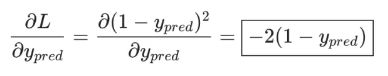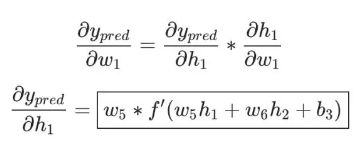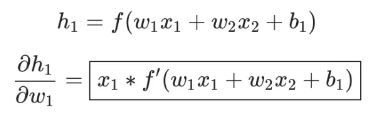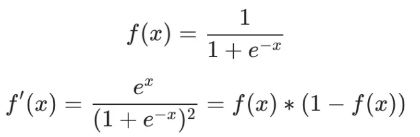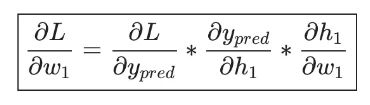神经网络初探

一、从人脑神经元到人工神经网络

仿生学是通过分析生物系统的特质，再通过工程技术进行实现并有效利用生物功能的一门学科，例如：蝙蝠-雷达。

树突用来接受信息的输入，一个神经元有多个树突，经过细胞核处理加工后，得出的结果通过轴突，突触输出，只有一个轴突，多个突触。当神经元与其他神经元相连，当它兴奋时，就会向相连的神经元发送化学物质，从而改变这些神经元的电位，当电位超过了一个阈值，那么它就会被激活，即兴奋，传递化学物质。

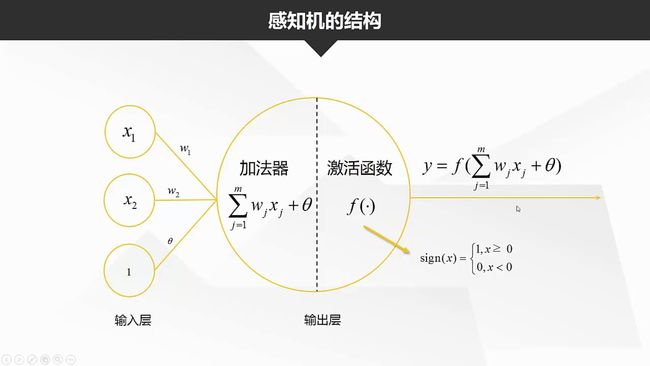
经过加法器，接收到总输入值，与神经元的阈值进行比较，然后通过激活函数处理以阐述神经元的输出。

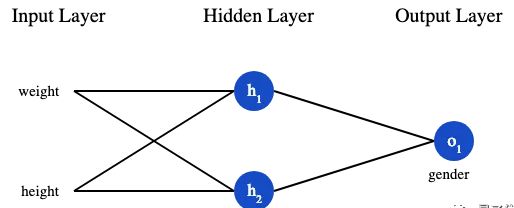
输入层只负责接收信息，一般3个x，加上一个常数项，输出层一般有2个节点，如果没有隐藏层，则为感知机。

把神经元的输入向前传递获得输出的过程称为前馈（feedforward）。

二、感知机

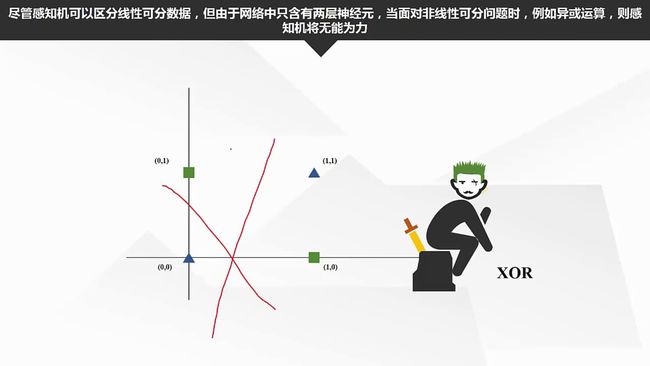
感知机是神经网络和支持向量机的基础，支持向量机对分离超平面增加约束条件，即间隔最大，和核技巧。而神经网络是增加了隐藏层。

激活函数的作用是将无限制的输入转换为可预测形式的输出。感知机的激活函数是阶跃函数。一般常见的还有sigmod函数,将可能在较大范围内变化的输入值挤压到（0，1）输出值范围内。也称为挤压函数。

三、bp神经网络

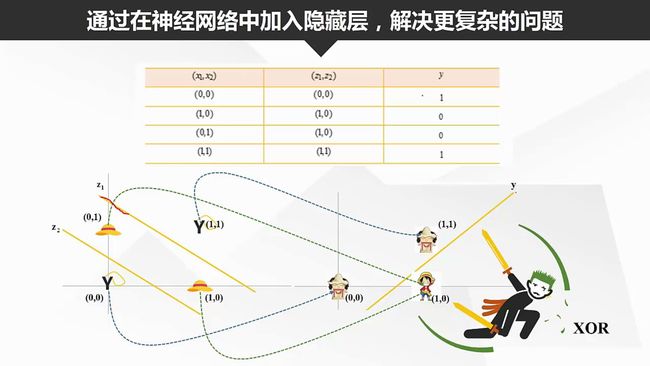
在感知机的基础上加入隐藏层，构造多个超平面，可以解决非线性可分问题。隐藏层和输出层神经元都是拥有激活函数的功能神经元。

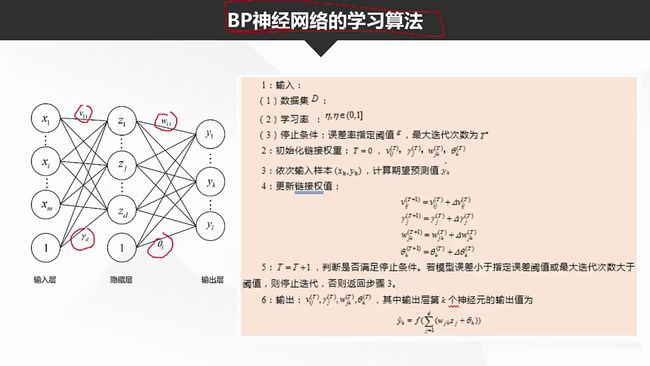
神经网络的学习过程，就是根据训练数据莱调整神经元之间的连接权和每个功能神经元的阈值。

简单来讲，“神经网络”就是通过输入多个非线性模型以及不同模型之间的加权互联（加权的过程在隐蔽层完成），最终得到一个输出模型。其中，隐蔽层所包含的就是非线性函数。

由于“神经网络”拥有特有的大规模并行结构和信息的并行处理等特点，因此它具有良好的自适应性、自组织性和高容错性，并且具有较强的学习、记忆和识别功能。目前神经网络已经在信号处理、模式识别、专家系统、预测系统等众多领域中得到广泛的应用。

“神经网络”的主要缺点就是其知识和结果的不可解释性，没有人知道隐蔽层里的非线性函数到底是如何处理自变量的，“神经网络”应用中的产出物在很多时候让人看不清其中的逻辑关系。但是，它的这个缺点并没有影响该技术在数据化运营中的广泛应用，甚至可以这样认为，正是因为其结果具有不可解释性，反而更有可能促使我们发现新的没有认识到的规律和关系。

四、训练神经网络

学习如何训练它，其实这就是一个优化的过程。假设有一个数据集，包含4个人的身高、体重和性别：

现在我们的目标是训练一个网络，根据体重和身高来推测某人的性别。为了简便起见，我们将每个人的身高、体重减去一个固定数值，把性别男定义为1、性别女定义为0。

在训练神经网络之前，我们需要有一个标准定义它到底好不好，以便我们进行改进，这就是损失（loss）。比如用均方误差（MSE）来定义损失：

n是样本的数量，在上面的数据集中是4；y代表人的性别，男性是1，女性是0；ytrue是变量的真实值，ypred是变量的预测值。顾名思义，均方误差就是所有数据方差的平均值，我们不妨就把它定义为损失函数。预测结果越好，损失就越低，训练神经网络就是将损失最小化。

如果上面网络的输出一直是0，也就是预测所有人都是男性，那么损失是：

MSE= 1/4 (1+0+0+1)= 0.5

五、减少神经网络损失

这个神经网络不够好，还要不断优化，尽量减少损失。我们知道，改变网络的权重和偏置可以影响预测值，但我们应该怎么做呢？

为了简单起见，我们把数据集缩减到只包含Alice一个人的数据。于是损失函数就剩下Alice一个人的方差：

预测值是由一系列网络权重和偏置计算出来的：

所以损失函数实际上是包含多个权重、偏置的多元函数：

如果调整一下w1，损失函数是会变大还是变小？我们需要知道偏导数∂L/∂w1是正是负才能回答这个问题。

根据链式求导法则：

而L=(1-ypred)2，可以求得第一项偏导数：

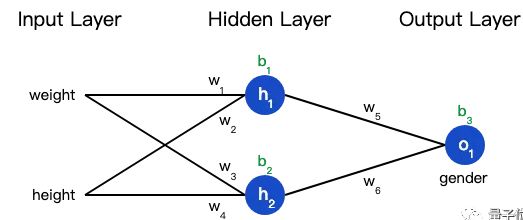
接下来我们要想办法获得ypred和w1的关系，我们已经知道神经元h1、h2和o1的数学运算规则：

实际上只有神经元h1中包含权重w1，所以我们再次运用链式求导法则：

然后求∂h1/∂w1

我们在上面的计算中遇到了2次激活函数sigmoid的导数f′(x)，sigmoid函数的导数很容易求得：

总的链式求导公式：

这种向后计算偏导数的系统称为反向传播（backpropagation）。

上面的数学符号太多，下面我们带入实际数值来计算一下。h1、h2和o1

h1=f(x1⋅w1+x2⋅w2+b1)=0.0474

h2=f(w3⋅x3+w4⋅x4+b2)=0.0474

o1=f(w5⋅h1+w6⋅h2+b3)=f(0.0474+0.0474+0)=f(0.0948)=0.524

神经网络的输出y=0.524，没有显示出强烈的是男（1）是女（0）的证据。现在的预测效果还很不好。

我们再计算一下当前网络的偏导数∂L/∂w1：

这个结果告诉我们：如果增大w1，损失函数L会有一个非常小的增长。

改进：随机梯度下降

下面将使用一种称为随机梯度下降（SGD）的优化算法，来训练网络。

经过前面的运算，我们已经有了训练神经网络所有数据。但是该如何操作？SGD定义了改变权重和偏置的方法：

η是一个常数，称为学习率（learning rate），它决定了我们训练网络速率的快慢。将w1减去η·∂L/∂w1，就等到了新的权重w1。

当∂L/∂w1是正数时，w1会变小；当∂L/∂w1是负数 时，w1会变大。

如果我们用这种方法去逐步改变网络的权重w和偏置b，损失函数会缓慢地降低，从而改进我们的神经网络。

训练流程如下：

1、从数据集中选择一个样本；

2、计算损失函数对所有权重和偏置的偏导数；

3、使用更新公式更新每个权重和偏置；

4、回到第1步。

(转自：https://mp.weixin.qq.com/s/JrLcPFVX6_uui-bfLHRefg，内含代码）