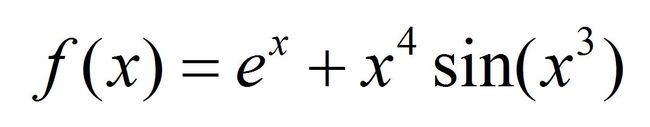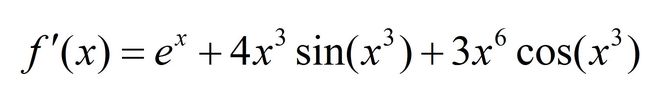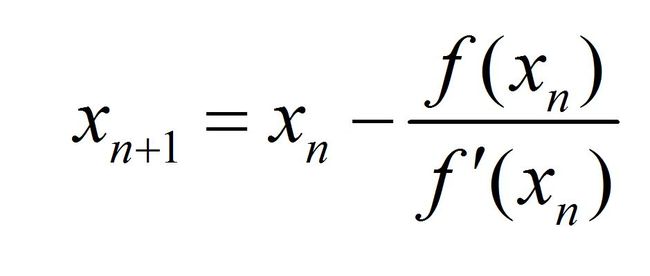使用牛顿迭代法求方程的根

第二篇随笔

9102年11月底,工科男曹**要算一个方程f(x)=0的根,其中f(x)表达式为:

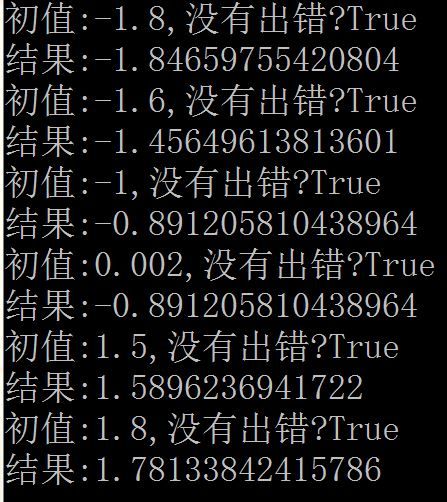
因为实数范围内f(x)=0的根太多,所以本文只研究-2

这个式子更丑,但是,我们有牛顿迭代法,可以构造迭代序列{xn}满足:

其中f'(xn)不等于0.可以证明,只要初值选的好,序列可以收敛到要求的根.然后就可以写程序求根了.

先上函数图像(由desmos绘制),看到指定区间上有5个零点.然后,零点附近取值吧.

再上效果

 

结果还是不错的.

最后,上代码.f(x)和f'(x)用委托的方式传入calc函数.委托注意实例化

Public Delegate Function myfunc(x As Double) As Double

Public Function func0(x As Double) As Double
    Return Exp(x) + Pow(x, 4) * Sin(Pow(x, 3))
End Function
Public Function func0derive(x As Double) As Double
    Return Exp(x) + 4 * Pow(x, 3) * Sin(Pow(x, 3)) + 3 * Pow(x, 6) * Cos(Pow(x, 3))
End Function

Dim f0 As New myfunc(AddressOf func0)
Dim fd0 As New myfunc(AddressOf func0derive)

 

calc的参数中f和fd分别是指向f(x)和f'(x)的函数指针,x0为初值,eps为精度,cnt为迭代次数

用传引用的方式,通过sol返回计算结果.

返回True为没有出错,False为出错.

 1 Public Function Calc(f As myfunc, fd As myfunc, x0 As Double, eps As Double, cnt As Integer, ByRef sol As Double) As Boolean
 2         If cnt <= 0 Or f Is Nothing Or fd Is Nothing Then
 3             Return False
 4         End If
 5         Try
 6             sol = 0
 7             Dim x As Double = x0, c0 As Integer = 0
 8             While Math.Abs(x) > eps And cnt > c0
 9                 x = x - f(x) / fd(x)
10                 c0 += 1
11             End While
12             sol = x
13             Return True
14         Catch ex As Exception
15             Return False
16         End Try
17     End Function