决策树和随机森林既可以解决分类问题,也可以解决预测问题。
随机森林的构建有两个方面:数据的随机性选取,以及待选特征的随机选取。
数据的随机选取:
第一,从原始的数据集中采取有放回的抽样,构造子数据集,子数据集的数据量是和原始数据集相同的。不同子数据集的元素可以重复,同一个子数据集中的元素也可以重复。
第二,利用子数据集来构建子决策树,将这个数据放到每个子决策树中,每个子决策树输出一个结果。最后,如果有了新的数据需要通过随机森林得到分类结果,就可以通过对子决策树的判断结果的投票,得到随机森林的输出结果了。
待选特征的随机选取:
与数据集的随机选取类似,随机森林中的子树的每一个分裂过程并未用到所有的待选特征,而是从所有的待选特征中随机选取一定的特征,之后再在随机选取的特征中选取最优的特征。这样能够使得随机森林中的决策树都能够彼此不同,提升系统的多样性,从而提升分类性能。
随机森林属于集成算法,森林从字面理解就是由多棵决策树构成的集合,而且这些子树都是经过充分生长的CART树;随机表示构成多棵决策树的数据是随机生成的,生成过程采用的是Bootstrap抽样法,运行速度快,预测准确高。
随机性具体体现在:一、每棵树的训练样本随机;二、树中每个节点的分裂字段也是随机选择的,从而不容易产生过拟合。
优点:
决策树易于理解和解释,可以可视化分析,容易提取出规则;
计算复杂度不高,对中间值的缺失不敏感,可以处理不相关特征数据;
测试数据集时,运行速度比较快;
决策树可以很好的扩展到大型数据库中,同时它的大小独立于数据库大小;
不需要任何领域知识或参数假设。
缺点:
容易出现过拟合问题。
对缺失数据处理比较困难。
忽略数据集中属性的相互关联。
ID3 算法计算信息增益时结果偏向数值比较多的特征。
改进措施(主要解决过拟合问题):
对决策树进行剪枝,可以采用交叉验证法和正则化的方法;
使用基于决策树的 combination 算法,如 Bagging,Random Forest 等。
应用领域:
企业管理实践,企业投资决策,由于决策树很好的分析能力,在决策过程应用较多。
**随机森林的优点: **
可以处理高维数据,不同进行特征选择(特征子集是随机选择)
模型的泛化能力较强
训练模型时速度快,成并行化方式,即树之间相互独立
模型可以处理不平衡数据,平衡误差
最终训练结果,可以对特种额排序,选择比较重要的特征
随机森林有袋外数据(OOB),因此不需要单独划分交叉验证集
对缺失值、异常值不敏感
模型训练结果准确度高
相对Bagging能够收敛于更小的泛化误差
数据预处理
# 导入第三方模块
import pandas as pd
# 读入数据
Titanic = pd.read_csv('F:\Titanic.csv')
Titanic.shape
891个观测,12个变量
Titanic.head()
数据有下面几列:
PassengerId,乘客的标识符;
Survived,他(她)是否存活了下来,为因变量,1表示存活,0表示未存活
Pclass,舱室类别,也许 1 表示经济舱,2 表示商务舱,3 表示头等舱;
Name,乘客的名字;
Sex,性别;
Age,年龄;
SibSp,即兄弟姐妹(siblings)或配偶(spouses),表示在船上的兄弟姐妹以及配偶的数目;
Parch,即父母(Parents)或子女(Children),表示在船上的父母子女的数目;
Ticket,船票详情;
Cabin,舱号,NaN 表示未知;
Embarked,登船的起始地,S 表示南安普顿(Southampton),Q 表示皇后镇(Queenstown),C 表示瑟堡(Cherbourg)
PassengerID、Name、Ticket、Cabin无意义,此处删除
# 删除无意义的变量
Titanic.drop(['PassengerId','Name','Ticket','Cabin'], axis = 1, inplace = True)
#检查剩余自字是否含有缺失值,并按行统计缺失值个数
Titanic.isnull().sum(axis = 0)
数据清理中最常用的技术是填充缺失数据。可以用众数、平均数或中位数来填充缺失数据。选择这些数据没有绝对规则,可以一一尝试,然后看看它们的表现如何。但是根据经验来讲,分类数据只能用众数,连续数据可以用中位数或平均数
Age缺失比较多,不可用均值直接填充,按照性别对客户的缺失年龄分组填充
# 对Sex分组,用各组乘客的平均年龄填充各组中的缺失年龄
Titanic.Sex.unique()
fillna_Titanic = []
for i in Titanic.Sex.unique():
update = Titanic.loc[Titanic.Sex == i,].fillna(value = {'Age': Titanic.Age[Titanic.Sex == i].mean()}, inplace = False)
fillna_Titanic.append(update)
fillna_Titanic
Embarked缺失较少,此处用众数填充
Titanic = pd.concat(fillna_Titanic)
# 使用Embarked变量的众数填充缺失值
Titanic.fillna(value = {'Embarked':Titanic.Embarked.mode()[0]}, inplace=True)
Titanic.head()
将数据集中的离散变量Pclass、Sex、Embarked进行哑变量处理
以登船地数据为例——这是用 Q、S 或 C 填充的数据。Python 库不能处理这个,因为它只能处理数字。所以需要独热向量化(One Hot Vectorization)来处理,它可以把一列变成三列。用 0 或 1 填充 Embarked_Q、Embarked_S 和 Embarked_C,来表示这个人是不是从这个港口出发的。
# 将数值型的Pclass转换为类别型,否则无法对其哑变量处理
Titanic.Pclass = Titanic.Pclass.astype('category')
# 哑变量处理
dummy = pd.get_dummies(Titanic[['Sex','Embarked','Pclass']])
# 水平合并Titanic数据集和哑变量的数据集
Titanic = pd.concat([Titanic,dummy], axis = 1)
# 删除原始的Sex、Embarked和Pclass变量
Titanic.drop(['Sex','Embarked','Pclass'], inplace=True, axis = 1)
Titanic.head()
表中右边8个变量为哑变量
构建决策树模型
# 导入第三方包
from sklearn import model_selection
# 取出所有自变量名称
predictors = Titanic.columns[1:]
predictors
# 将数据集拆分为训练集和测试集,且测试集的比例为25%
X_train, X_test, y_train, y_test = model_selection.train_test_split(Titanic[predictors], Titanic.Survived,
test_size = 0.25, random_state = 1234)
为防止构建决策树过拟合,需进行预剪枝,限制树生长的最大深度,中间节点能够继续分支的最小样本量,叶节点的最小样本量
Python提供了网格搜索法,即调用GridSearch类选择最佳的参数组合
# 导入第三方模块
from sklearn.model_selection import GridSearchCV
from sklearn import tree
# 预设各参数的不同选项值
max_depth = [2,3,4,5,6]
min_samples_split = [2,4,6,8]
min_samples_leaf = [2,4,8,10,12]
# 将各参数值以字典形式组织起来
parameters = {'max_depth':max_depth, 'min_samples_split':min_samples_split, 'min_samples_leaf':min_samples_leaf}
parameters
# 网格搜索法,测试不同的参数值
grid_dtcateg = GridSearchCV(estimator = tree.DecisionTreeClassifier(), param_grid = parameters, cv=10)
# 模型拟合
grid_dtcateg.fit(X_train, y_train)
# 返回最佳组合的参数值
grid_dtcateg.best_params_
经过十重交叉验证,可得最佳组合值:3,4,2
# 导入第三方模块
from sklearn import metrics
# 构建分类决策树
CART_Class = tree.DecisionTreeClassifier(max_depth=3, min_samples_leaf = 4, min_samples_split=2)
# 模型拟合
decision_tree = CART_Class.fit(X_train, y_train)
decision_tree
# 模型在测试集上的预测
pred = CART_Class.predict(X_test)
pred
# 模型的准确率
print('模型在测试集的预测准确率:\n',metrics.accuracy_score(y_test, pred))
此时因变量为离散变量(分类变量),使用准确率指标
当因变量为连续型的数值,使用均方误差MSE或者均方根误差RMSE,越小代表拟合效果越好,即metrics.mean_squared_error(y_test,pred),在随机森林中类似,不再用准确率,也用MSE。即tree.DecisionTreeClassifier改为Regressor
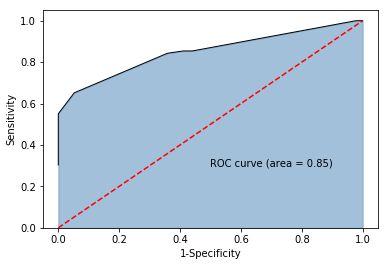
预测精度比较高,但无法体现正例和负例的覆盖率,为进一步验证模型在测试集上预测效果,绘制ROC曲线
# 导入第三方包
import matplotlib.pyplot as plt
y_score = CART_Class.predict_proba(X_test)[:,1]
fpr,tpr,threshold = metrics.roc_curve(y_test, y_score)
# 计算AUC的值
roc_auc = metrics.auc(fpr,tpr)
roc_auc
# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()
ROC曲线下的面积AUC为0.85,超过0.8,模型拟合效果比较好
下面将决策树进行可视化,需要在电脑中安装Graphviz, 然后将解压文件中的bin设置到环境变量中
# 导入第三方模块
from sklearn.tree import export_graphviz
from IPython.display import Image
import pydotplus
from sklearn.externals.six import StringIO
# 绘制决策树
dot_data = StringIO()
export_graphviz(
decision_tree,
out_file=dot_data,
feature_names=predictors,
class_names=['Unsurvived','Survived'],
# filled=True,
rounded=True,
special_characters=True
)
# 决策树展现
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())
构建随机森林模型
# 导入第三方包
from sklearn import ensemble
# 构建随机森林
RF_class = ensemble.RandomForestClassifier(n_estimators=200, random_state=1234)
# 随机森林的拟合
RF_class.fit(X_train, y_train)
# 模型在测试集上的预测
RFclass_pred = RF_class.predict(X_test)
# 模型的准确率
print('模型在测试集的预测准确率:\n',metrics.accuracy_score(y_test, RFclass_pred))
用随机森林确实提高了测试数据集上的预测准确率
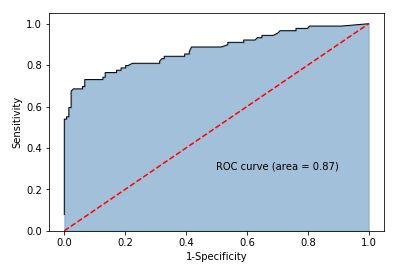
同样,也绘制ROC曲线
# 计算绘图数据
y_score = RF_class.predict_proba(X_test)[:,1]
fpr,tpr,threshold = metrics.roc_curve(y_test, y_score)
roc_auc = metrics.auc(fpr,tpr)
# 绘图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
plt.plot(fpr, tpr, color='black', lw = 1)
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
plt.show()
AUC的值为0.87,同样比单棵决策树的AUC高
再挑选出重要因素
# 变量的重要性程度值
importance = RF_class.feature_importances_
# 构建含序列用于绘图
Impt_Series = pd.Series(importance, index = X_train.columns)
# 对序列排序绘图
Impt_Series.sort_values(ascending = True).plot('barh')
plt.show()
年龄,票价,是否为女性是最重要的前三个因素,从而在一定程度上体现妇女和儿童优先的原则