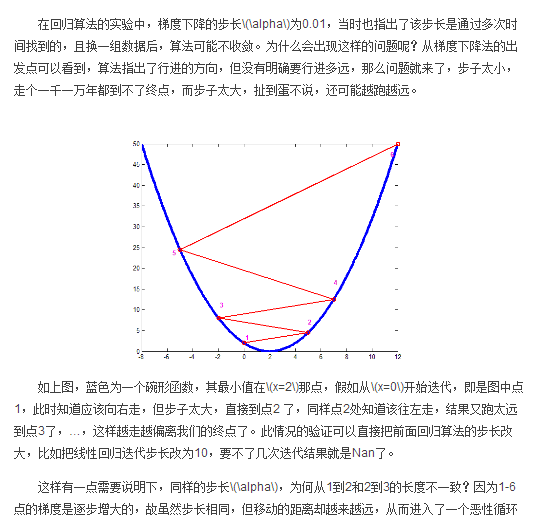
梯度下降法的搜索方向顾名思义就是梯度方向,也就是当前点所在地形最陡峭的下降方向(你这个图里面只有左右两个方向)。
步长的选择要看函数的性质,一般可导函数,只要步长足够小,则保证每次函数值都不会增加,此外:
1. 如果函数可导,且函数的梯度满足李普希兹连续(常数为L),若以小于(1/L)的步长迭代,则能保证每次迭代的函数值都不增,则保证最终会收敛到梯度为0的点。也可以采用Line search确定步长,Line search的本质目的其实也是为了保证函数值下降(或称作不增)。
2. 如果函数还是凸的,则最终会走到最优点。
作者:li Eta
来源:知乎
链接:https://www.zhihu.com/question/37911687/answer/74529437
对于full gradient方法,一般都是line search,基本思想就是每次试一个步长,如果用该步长走的话,看函数值会不会比当前点下降一定的程度,如果没有,就按比例减小步长,再试,直到满足条件(根据泰勒展开式我们知道步长足够小时总会满足下降条件)。所以line search实际上是计算量比较大的,不过在以前数据量不大的情况下这都不是问题。关于line search,我觉得[1]写的极好。
此外,还有一种方法叫Barzilai-Borwen方法(简称BB,[2]),这种方法源自拟牛顿法,非常简单,基本不用额外计算也可以很好的估计步长。这个方法缺点就是,有可能不收敛,所以一般的用法是先用BB算一个步长、再从这个步长出发用line search,这样可以大大减少line search的次数。关于BB法可以推荐看综述[3]。
对于SGD,普通的line search计算量太大根本不可能。目前没有非常成熟的办法,实际中还是靠手动调步长。当然,最近几年也有一些工作:
最有名的是AdaGrad和改进版的AdaDelta,这两个方法有用,至少可以确保收敛,但速度上不够好,远不如手动调的最好步长,特别迭代次数多了之后。当然他们的优点就是在不怎么要手动调参、基本不用额外计算量的情况下收敛的还可以。
[4] 中有提出过一种简化版line search方法。这种方法每轮迭代只用一个子函数做一次line search来估计Lipschitz常数L,然后选择理论上最好的步长,比如说1/L,这样相对计算量还可以接受了。但这个方法有两个问题:一是只能用在SAG、SVRG这种固定步长能保证收敛的算法上,原始的SGD不行;第二就是,就算知道了L,但实际中最佳步长和理论最佳往往差了很远。但总的来说,根据我实验观察,这是种比较靠谱的方法。
[5] 提出了一种probabilistic line search。基本思想就是在每个迭代点计算一个子函数的值,然后用Gaussian Process来做拟合,给出目标函数在每个的估计值,然后利用这个估计值来做line search。我自己没有亲自实验过这种方法,但个人感觉就是计算量仍然偏大(除了每次迭代要计算一个函数值,还要要不断计算和更新一个Gaussian process),而且感觉不一定能收敛。
[6] 是做SGD步长估计的,几个月前才出炉的paper。大概思想是假设步长服从某个简单的函数,比如
(因为SGD需要diminishing的步长来保证收敛),这儿k是指第几轮迭代,C是某个我们要估计的常数。然后在每轮迭代的时候用online梯度下降的方法更新下对C的估计。但是这篇paper实验做的巨简单无比,不太清楚这个方法到底咋样。最后,我最近有篇paper关于这个问题,等发了再说。
参考文献:
[1] Nocedal, Jorge, and Stephen Wright.Numerical optimization. Springer Science & Business Media, 2006.
[2] Fletcher, R. (2005). On the barzilai-borwein method. InOptimization and control with applications(pp. 235-256). Springer US.
[3] Raydan, Marcos. "On the Barzilai and Borwein choice of steplength for the gradient method."IMA Journal of Numerical Analysis13.3 (1993): 321-326.
[4] Roux, Nicolas L., Mark Schmidt, and Francis R. Bach. "A stochastic gradient method with an exponential convergence _rate for finite training sets."Advances in Neural Information Processing Systems. 2012.
[5] Mahsereci, Maren, and Philipp Hennig. "Probabilistic line searches for stochastic optimization."Advances In Neural Information Processing Systems. 2015.
[6] Massé, Pierre-Yves, and Yann Ollivier. "Speed learning on the fly."arXiv preprint arXiv:1511.02540(2015).
作者:Martin Tan
链接:https://www.zhihu.com/question/37911687/answer/93944721
来源:知乎