1 The Purposes
- Get familiar with the common ANN algorithms, such as KD-Tree and LSH
- Learn the implementation of LSH and other related coding skills
- Analysis the performance of KD-Tree and LSH under different dimensions
2 The Principles
2.1 ANN
Efficient and accurate methods for Approximate Near-NearestNeighbor (ANN) queries are important for large-scale datasetsapplications such as image feature matching, recommendation system,DNA sequencing and so on.
Popular ANN methods include randomized kd-tree(KD-Tree),hierarchical k-means(HKM) and locality-sensitive hashing(LSH).
2.1.1 KDT
KDT partition a vector space by recursively generatinghyperplanes and cut along coordinates where there is maximal variancein the data. KD-Tree is good for searching in low-dimensional spaceswhile its efficiency decreases as dimensionality grows over than 10generally.
- Building a kd-tree: O(N*logN) for time and O(N) for space
- Nearest neighbor search: O(logN)
- M nearest neighbors: O(M*logN)
2.1.2 LSH
LSH algorithm map similar input items to the same hash code withhigher probability than dissimilar items. For a given key size K, wegenerate randomized hyperplanes and check if a point P is above orbelow the hyperplanes. Assigning 0/1 based on below/above checking.And then perform harmming distance search on K bit for approximatenearest neighbors.
- Build a LSH table: O(N*K) for time and O(N) for space, K is the key size
- Nearest neightbor search: O(1) for the best situation
2.2 Related Open Source Projects
FLANNis a library for performing fast approximate nearest neighborsearches in high dimensional spaces. It contains a collection ofalgorithms we found to work best for nearest neighbor search and asystem for automatically choosing the best algorithm and optimumparameters depending on the dataset.
LsHash is an open source project on Github and implement a fast pythonlocality sensitive hashing with persistance support.
Webenchmark our KD-Tree performance based on FLANN and pyflann project.The dynamic library libflann.so is compiled and linked bypyflann python bindings. Our Lsh algorithm is based on LsHash andsome modifications are made.
2.3 Datasets
2.3.1 SIFT10K
SIFT10K dataset contains 128 dimensionalities of SIFT feature. Itcomprises up to 10 thousand of data vectors and one hundred of queryvectors. For each query vector, the ground truth file is also givenwith top k=100 nearest neighbors.
2.3.3 SIFT1M
SIFT1M dataset contains 128 dimensionalities of SIFT feature. Itcomprises up to 1 million of data vectors and 10 thousand of queryvectors. For each query vector, the ground truth file is also givenwith top k=100 nearest neighbors.
2.3.3 GIST1M
GIST dataset contains 960 dimensionalities of GIST feature. Itcomprises up to 1 million of data vectors and one thousand of queryvectors. For each query vector, the ground truth file is also givenwith top k=100 nearest neighbors.
2.4 Measure
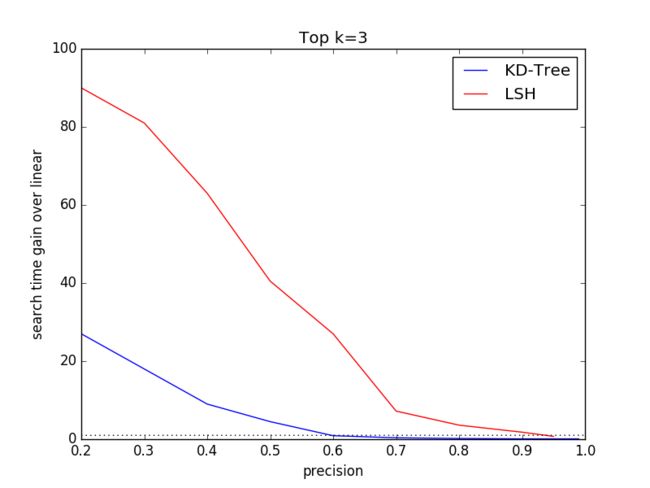
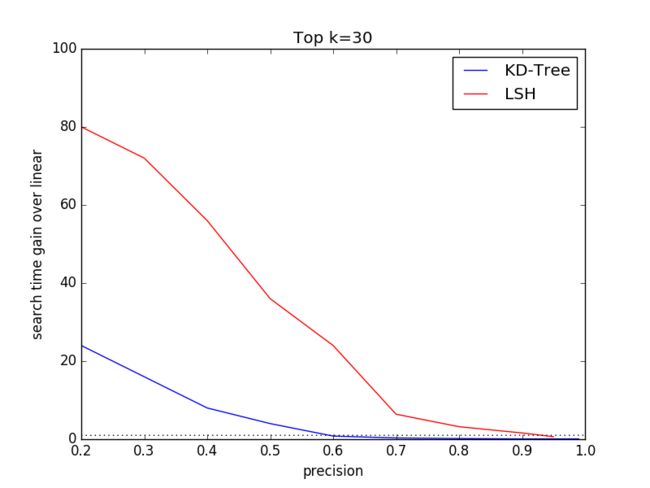
We choose 3 main factors to benchmark performance of KD-Tree andLSH. Precesion can be seen as a measure of exactness or quality andtime/memory cost are also taken into account.
For each expriment, we will plot the two (x,y) lines underdifferent different algorithms, where y is the search time gain overlinear search time and x is the corresponding precision. Theprecision is the average precision of all query points.
Regarding expriment figure may like Fig.1 :
3 The Procedures
This is the machine configuration:
- Ubuntu 16.04, 64 bit, with Intel Core i7-4970K 4.0GHz x8 and 16GB RAM
- Main programming language: Python2.7 & C11++
- FLANN 1.8.4 and pyflann bindings
- LSH implementation via python based on open source LsHash
3.1 Data Dimensionality
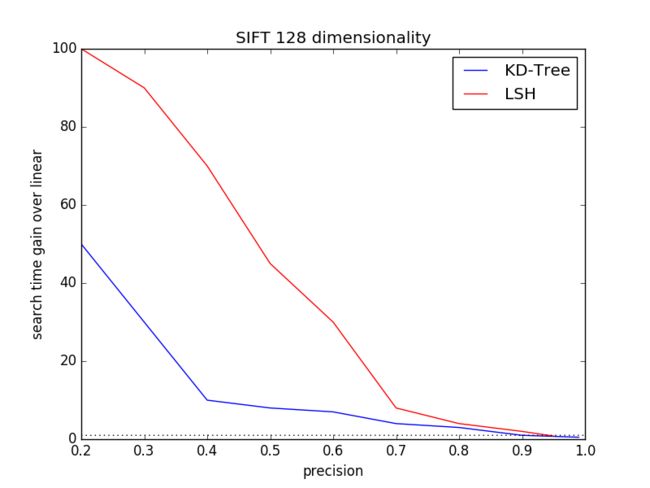
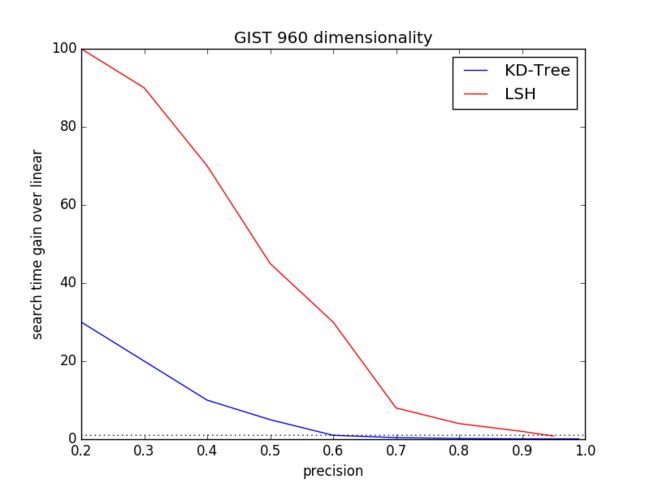
The Startdard dataset SIFT1M contains 128 dimensionality of SIFTfeature and GIFT1M comprises 960 dimensionality of GIST feature. Wecompare the each performance of KD-Tree and LSH on dimension 128, 960respectively.
For KD-Tree, the parameters include Kd-tree number K and how manyleafs to visit when searching for neighbors, namely Checks. For LSH,the parameters include table number L and key size.
For each dimension, we will calculate the distribution of(precision, search time gain over linear) and plot it using pythonmatplotlib.
Fig.2 and Fig.3 are the respecting expriement result.
Besides, we will calculate the memory cost on both 128 and 960dimentionality.
3.2 Dataset Size
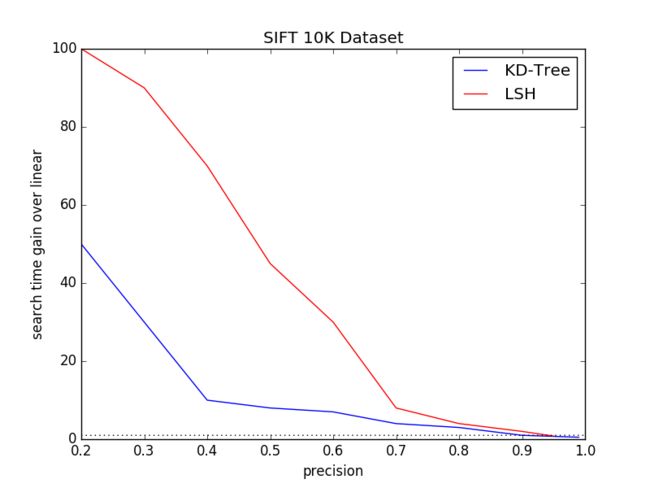
We select dataset size of 10K, 1M from standard dataset SIFT10Kand SIFT1M. We discard the GIST1M dataset as the GIST featuredimension varies. For better comparision, SIFT1B need to be takeninto account. However, it’s too large to run on my computer atpresent.
In this expriment, we will vary the tree number K, search leafsChecks for KD-Tree algorithm and table number L, key Size for LSHalgorithm to get the disbritution of (search time gain over linear,precision) under different dataset size.
Fig.2 and Fig.3 are the respecting expriement result.
Besides, we will calculate the memory cost on both 10K and 1Mdataset.
3.3 Varying k
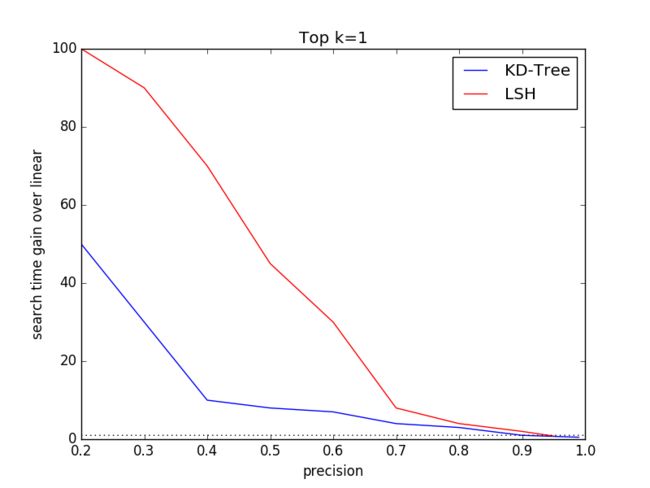
The ground truth dataset comprises top k=100 features for eachquery. To compare specific k performance of KD-Tree and LSHalgorithms, we select k=1, 3, 30, 100. We choose SIFT1M as thedataset and discard SIFT10K and GIST1M to keep the other dimensionsame other than different k.
In this expriment, we will vary the tree number K, search leafsChecks for KD-Tree algorithm and table number L, key Size for LSHalgorithm to get the disbritution of (search time gain over linear,precision) under different dataset size.
4 The Results
To be continued...
5 The Bibliography
[1]MariusMuja and David G. Lowe: Nearest Neighbor Algorithms for High Dimensional Data. Pattern Analysis and Machine Intelligence (PAMI), Vol. 36, 2014.
[2]A. Gionis, P. Indyk, and R. Motwani. Similarity search in highdimensions via hashing. In Proc. Int’l Conf. on Very Large DataBases (VLDB), 1999. 1, 2, 4
[3]Qin Lv, William Josephson, Zhe Wang, Moses Charikar, Kai Li.Multi-Probe LSH: Efficient Indexing for High-Dimensional SimilaritySearch. Proceedings of the 33rd International Conference on VeryLarge Data Bases (VLDB). Vienna, Austria. September 2007
[4]Marius Muja, David Lowe. FLANN - Fast Library for Approximate NearestNeighbors User Manual. January 24, 2013
[5]C. Silpa-Anan and R. Hartley. Optimised KD-trees for fast imagedescriptor matching. In Proc. Computer Vision and Pattern Recognition(CVPR), 2008. 1, 2
[6]IoannisZ. Emiris and DimitriNicolopoulos. Randomizedkd-trees for Approximate Nearest Neighbor Search.
November28, 2013
[7]JingdongWang, Heng Tao Shen, Jingkuan Song, and Jianqiu Ji. Hashing forSimilarity Search: A Survey.
arXiv:1408.2927v1[cs.DS] 13 Aug 2014
[8]MalcolmSlaney, Yury Lifshits and Junfeng He. Optimal Parameters for Locality-Sensitive Hashing.Proceedings of the IEEE, Vol. 100, No. 9, September 2012
[9]Nearest neighbor search. Wikipedia,https://en.wikipedia.org/wiki/Nearest_neighbor_search. Accessed 12 Oct 2016
[10]FLANN-Fast Library for Approximate Nearest Neighbors. University ofBritsh, http://www.cs.ubc.ca/research/flann/.Access 14 Oct 2016
[11]ALGLIB User Guide. ALGLIB Project,http://www.alglib.net/other/nearestneighbors.php.Accessed 14 Oct 2016
[12]Jason. LSH 算法框架分析. Web, http://blog.jasonding.top/2018/01/01/MLStick/ http://www.cnblogs.com/hxsyl/p/4626092.html.Access 11 Oct 2016
[13]坏人. LSH位置敏感哈希算法. CSDN, http://blog.csdn.net/u013378306/article/details/52473176,8 Sep 2016.