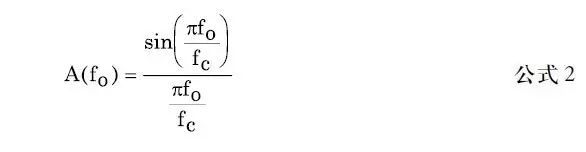姓名:徐娇 学号:17011210547
转自http://mp.weixin.qq.com/s/ZMTYubs8hUqlg_B2So-cdA
【嵌牛导读】随着数字技术在仪器仪表和通信系统中的广泛使用,可从参考频率源产生多个频率的数字控制方法诞生了,即直接数字频率合成(DDS)。DDS是一种采样数据系统,因此必须考虑所有与采样相关的问题,包括量化噪声、混叠、滤波等。例如,DAC输出频率的高阶谐波会折回奈奎斯特带宽,因而不可滤波,而基于PLL的合成器的高阶谐波则可以滤波。此外,还有其它几种因素需要考虑,稍后将会讨论。
【嵌牛鼻子】DDS系统、DDS构架基本原理
【嵌牛提问】DDS构架的基本原理及其影响因素?
【嵌牛正文】
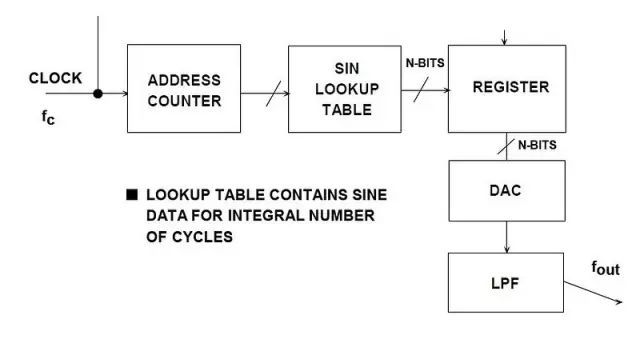
随着数字技术在仪器仪表和通信系统中的广泛使用,可从参考频率源产生多个频率的数字控制方法诞生了,即直接数字频率合成(DDS)。其基本架构如图1所示。该简化模型采用一个稳定时钟来驱动存储正弦波(或其它任意波形)一个或多个整数周期的可编程只读存储器(PROM)。
随着地址计数器逐步执行每个存储器位置,每个位置相应的信号数字幅度会驱动DAC,进而产生模拟输出信号。最终模拟输出信号的频谱纯度主要取决于DAC。相位噪声主要来自参考时钟。
DDS是一种采样数据系统,因此必须考虑所有与采样相关的问题,包括量化噪声、混叠、滤波等。例如,DAC输出频率的高阶谐波会折回奈奎斯特带宽,因而不可滤波,而基于PLL的合成器的高阶谐波则可以滤波。此外,还有其它几种因素需要考虑,稍后将会讨论。
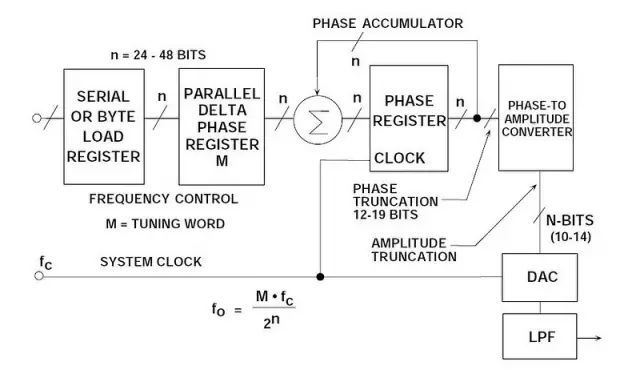
这种简单DDS系统的基本问题在于,最终输出频率只能通过改变参考时钟频率或对PROM重新编程来实现,非常不灵活。实际DDS系统采用更加灵活有效的方式来实现这一功能,即采用名为数控振荡器(NCO)的数字硬件。图2所示为该系统的框图。
系统的核心是相位累加器,其内容会在每个时钟周期更新。相位累加器每次更新时,存储在△相位寄存器中的数字字M就会累加至相位寄存器中的数字。假设△相位寄存器中的数字为00...01,相位累加器中的初始内容为00...00。相位累加器每个时钟周期都会按00...01更新。如果累加器为32位宽,则在相位累加器返回至00...00前需要232(超过40亿)个时钟周期,周期会不断重复。
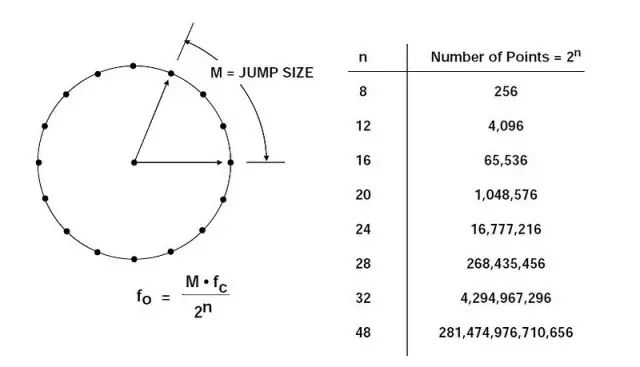
相位累加器的截断输出用作正弦(或余弦)查找表的地址。查找表中的每个地址均对应正弦波的从0°到360°的一个相位点。查找表包括一个完整正弦波周期的相应数字幅度信息。(实际上,只需要90°的数据,因为两个MSB中包含了正交数据)。因此,查找表可将相位累加器的相位信息映射至数字幅度字,进而驱动DAC。图3用图形化的“相位轮”显示了这一情况。
考虑n = 32,M = 1的情况。相位累加器会逐步执行232个可能的输出中的每一个,直至溢出并重新开始。相应的输出正弦波频率等于输入时钟频率232分频。若M=2,相位累加器寄存器就会以两倍的速度“滚动”计算,输出频率也会增加一倍。以上内容可总结如下:
n位相位累加器(大多数DDS系统中,n的范围通常为24至32)存在2n个可能的相位点。△相位寄存器中的数字字M代表相位累加器每个时钟周期增加的数量。如果时钟频率为fc,则输出正弦波频率计算公式为:
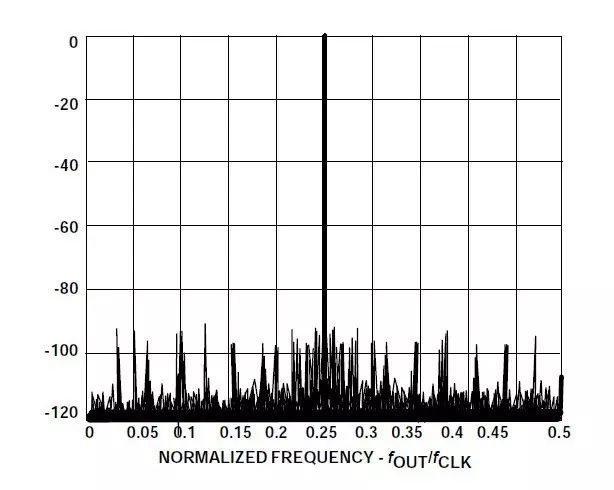
该公式称为DDS“调谐公式”。注意,系统的频率分辨率等于fc/2n。n = 32时,分辨率超过40亿分之一!在实际DDS系统中,溢出相位寄存器的位不会进入查找表,而是会被截断,只留下前13至15个MSB。这样可以减小查找表的大小,而且不会影响频率分辨率。相位截断只会给最终输出增加少量可接受的相位噪声。(参见图4)。
DAC的分辨率通常比查找表的宽度少2至4位。即便是完美的N位DAC,也会增加输出的量化噪声。图4显示的是32位相位累加器15位相位截断时计算得出的输出频谱。选择M值后,输出频率会从0.25倍时钟频率开始稍有偏移。注意,相位截断和有限DAC分辨率产生的杂散都至少比满量程输出低90 dB。这一性能远远超出了任何商用12位DAC,足以满足大多数应用的需求。
上述基本DDS系统极为灵活,且具有高分辨率。只需改变M寄存器的内容,频率就可以立即改变,不会出现相位不连续。但是,实际DDS系统首先需要执行串行或字节加载序列,以将新的频率字载入内部缓冲寄存器,然后再载入M寄存器。这样就可以尽可能减少封装引脚数。新的频率字载入缓冲寄存器后,并行输出△相位寄存器就会同步操作,从而同时改变所有位。加载△相位缓冲寄存器所需的时钟周期数决定了输出频率的最大改变速率。
DDS系统中的混叠
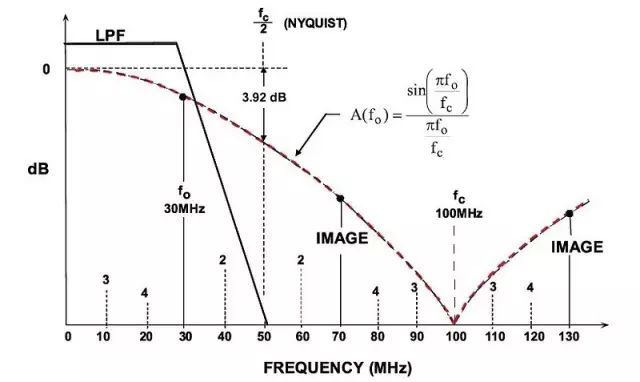
简单DDS系统中可能会产生一种重要的输出频率范围限制。奈奎斯特准则表明,时钟频率(采样速率)必须至少为输出频率的两倍。实际最高输出频率限制在约1/3时钟频率范围内。图5所示为DDS系统中的DAC输出,其中输出频率为30 MHz,时钟频率为100 MHz。如图所示,重构DAC后必须跟随一个抗混叠滤波器,以消除较低的图像频率(100 – 30 = 70 MHz)。
注意,DAC输出(滤波前)的幅度响应跟随着一个sin(x)/x响应,在时钟频率及其整数倍时,该值为零。归一化输出幅度A(fO)的精确计算公式如下:
其中,fO为输出频率,fc为时钟频率。
出现该滚降的原因是由于DAC输出并非一系列零宽脉冲(和最佳重新采样器中一样),而是一系列矩形脉冲,宽度等于更新速率的倒数。sin(x)/x响应的幅度比奈奎斯特频率低3.92 dB(DAC更新速率的1/2)。实际上,抗混叠滤波器的传递函数可用来补偿sin(x)/x滚降,使整体频率响应相对平坦,达到最大输出DAC频率(一般为1/3更新速率)。
另一个重要的考虑因素在于,和基于PLL的系统不同,DDS系统中的基本输出频率高阶谐波会因混叠而折回至基带。这些谐波无法通过抗混叠滤波器去除。例如,如果时钟频率为100 MHz,输出频率为30 MHz,则30 MHz的第二个谐波会出现在60 MHz(带外),但也会出现在100 – 60 = 40 MHz(混叠成分)。同样,第三个谐波(90 MHz)会出现在带内,频率为100 – 90 = 10 MHz,第四个谐波出现在120 – 100 MHz = 20 MHz。高阶谐波也会落在奈奎斯特带宽内(直流至fc/2)。前4个谐波的位置如图所示。
用作ADC时钟驱动器的DDS系统
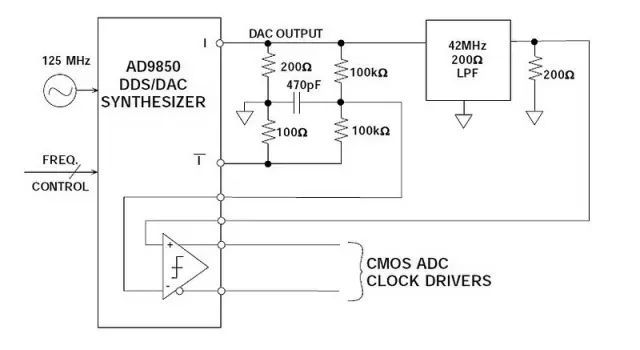
DDS系统(如AD9850)可以提供产生ADC采样时钟的出色方法,尤其适合ADC采样频率必须受到软件控制,且锁定至系统时钟的情况(参见图6)。DAC输出电流IOUT驱动200 Ω、42 MHz的低通滤波器,源和负载阻抗端接,等效负载为100 Ω。滤波器可以消除42 MHz以上的杂散频率成分。经过滤波的输出可以驱动AD9850内部比较器的一个输入端。DAC补偿输出电流可以驱动100 Ω的负载。位于两个输出之间的100 kΩ电阻分压器输出经过去耦,可以产生参考电压以供内部比较器使用。
比较器输出有2 ns的上升和下降时间,可以产生与TTL/CMOS逻辑电平兼容方波。比较器输出边缘的抖动小于20 ps rms。输出和补偿输出均可按要求提供。
在图6所示的电路中,40 MSPS ADC时钟的总输出均方根抖动为50 ps rms,由此产生的信噪比下降在宽动态范围应用中必须加以考虑。
DDS系统中的幅度调制
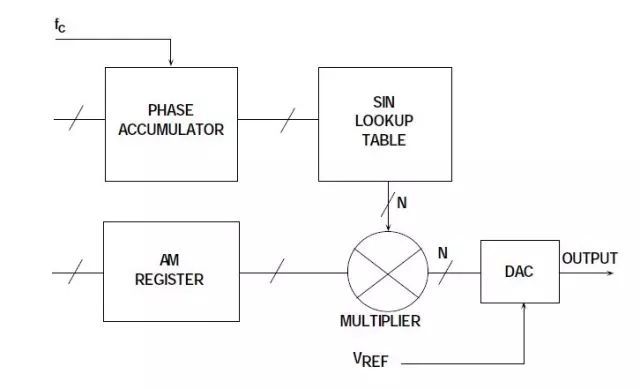
DDS系统中的幅度调制可以通过在查找表和DAC输入之间放置数字乘法器来实现,如图7所示。调制DAC输出幅度的另一种方法是改变DAC的参考电压。在AD9850中,内部参考控制放大器的带宽约为1 MHz。这种方法在输出幅度变化相对较小的情况下非常有效,只要输出信号不超过+1 V的规格即可。
DDS系统中的无杂散动态范围考虑
在大多数DDS应用中,首要考虑因素是DAC输出的频谱纯度。遗憾的是,该性能的测量、预测和分析十分复杂,涉及大量相互作用的因素。
即便是理想的N位DAC,也会在DDS系统中产生谐波。这些谐波的幅度主要取决于输出频率与时钟频率的 比值。原因在于,DAC量化噪声的频谱成分会随着该比值的变化而变化,虽然其理论均方根值仍等于q/√12(其中q是LSB的权重)。“量化噪声表现为白噪声,在奈奎斯特带宽内均匀分布”这条假设在DDS系统中并不适用(这条假设在ADC系统中更为适用,因为ADC会给信号增加一定的噪声,从而“扰动”量化误差或使其随机化。
但是,依然存在一定的相关性)。例如,如果DAC输出频率精确设置为时钟频率的约数,则量化噪声会集中在输出频率的倍数,也就是说,主要取决于信号。如果输出频率稍有失调,量化噪声会变得更加随机,从而改进有效SFDR。
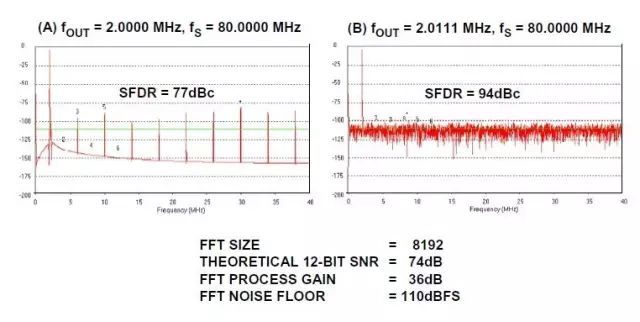
图8说明了上述情况,其中4096 (4k)点FFT基于理想12位DAC中数字化生成的数据计算得出。左侧图表(A)中,所选的时钟频率和输出频率的比值恰好等于40,获得的SFDR约为77 dBc。右侧图表中,比例稍有失调,有效SFDR增至94 dBc。在这一理想情况下,只是略微改变了频率比,SFDR就改变了17 dB。
因此,通过仔细选择时钟与输出频率,就可以获得最佳SFDR。但是,在有些应用中,这点可能难以实现。在基于ADC的系统中,增加少量的随机噪声至输入就可能使量化误差随机化,并且减少这种效应。
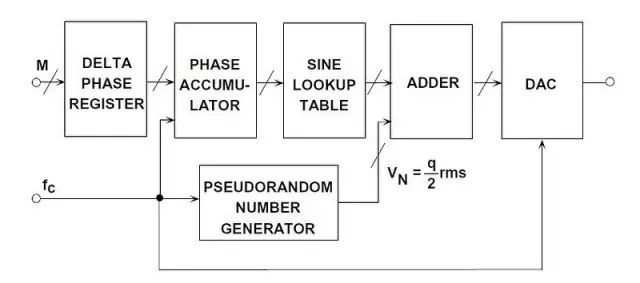
DDS系统中也可以实现同样的效果,如图9所示。伪随机数字噪声发生器输出先增加至DDS正弦幅度字,然后再载入DAC。数字噪声的幅度设置为1/2 LSB左右。这样就能实现随机化过程,代价是整体输出本底噪声会略微增加。但是,在大多数DDS系统中,有足够的灵活性可以选择不同的频率比,因此不需要扰动。