机器学习 | 优化——梯度下降（Gradient Descent）

写在前面：

在求解机器学习算法的模型参数，即 无约束优化问题 时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法，当然还有其他的方式。

下文主要是对梯度下降进行总结，其中很多文字均不是自己写的，仅作为学习笔记的整理。

本文主要是对 梯度下降（Gradient Descent）小结 这篇文章的文字搬运，如若侵权，还望告知，侵删！！！

1. 梯度：

在微积分里面，对多元函数的参数求偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。

比如函数, 分别对求偏导数，求得的梯度向量就是 ,简称 或者。

对于在点的具体梯度向量就是 或者 。

如果是个参数的向量梯度，就是 ，以此类推。

那么这个 梯度向量 求出来有什么意义呢？

从几何意义上讲，其意义就是 函数变化增加最快的地方。具体来说，对于函数f(x,y),在点(x_0,y_0)，沿着梯度向量的方向就是的方向是增加最快的地方。或者说，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，也就是 的方向，梯度减少最快，也就是更加容易找到函数的最小值。

——参考：梯度下降（Gradient Descent）小结

2. 梯度下降与梯度上升：

在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。

梯度下降法和梯度上升法是可以互相转化的。比如我们需要求解损失函数的最小值，这时我们需要用梯度下降法来迭代求解。但是实际上，我们可以反过来求解损失函数的最大值，这时梯度上升法就派上用场了。
（就好比求解最大值和求解最小值可以相互转化一样）

3. 梯度下降：

3.1 直观理解：

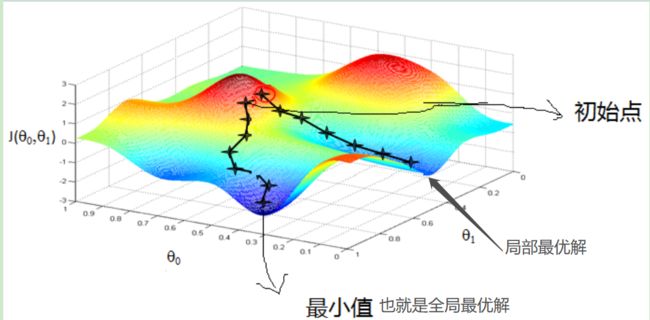
首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。

从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

参考：梯度下降（Gradient Descent）小结

还可以看一下这篇文章：tensorflow-梯度下降,有这一篇就足够了，更好理解梯度下降。

3.2 相关概念：

• 步长（Learning rate）：也称为学习率。步长决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。
  用上面下山的例子，步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。

• 特征（feature）：指的是样本中输入部分，比如个 单个特征 的样本,，则第一个样本特征为，第一个样本输出为。

• 假设函数（hypothesis function）：在监督学习中，为了拟合输入样本，而使用的假设函数，记为。
  比如对于 单个特征 的个样本，可以采用拟合函数如下： 。

• 损失函数（loss function）：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方。
  比如对于m个样本，采用 线性回归，损失函数为：其中表示第个样本特征，表示第个样本对应的输出，为假设函数。

3.3 详细描述（代数方式）：

4. 梯度下降大家族：BGD、SGD、MBGD

5. 代码实现：

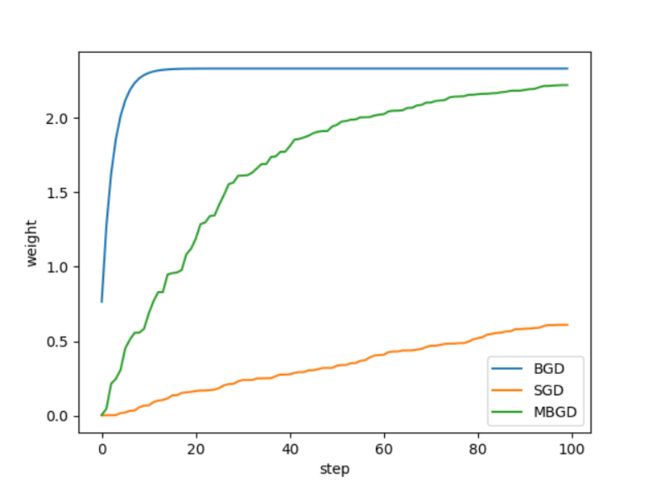
5.1 BGD、SGD、MBGD直观比较：

# encoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
# 创建训练数据集
# 假设训练学习一个线性函数 y=2.33x
EXAMPLE_NUM = 100# 样本总数
BATCH_SIZE = 10# mini_batch训练集大小
TRAIN_STEP = 100# 训练次数
LEARNING_RATE = 0.0001# 学习率
X_INPUT = np.arange(EXAMPLE_NUM) * 0.1# 生成输入数据 X
Y_OUTPUT_CORRECT = 2.33 * X_INPUT# 生成训练正确输出数据
 
def train_func(X, K):
    result = K * X
    return result

# BGD
# 参数初始化值
k_BGD = 0.0
# 记录迭代数据用于作图
k_BGD_RECORD = []
for step in range(TRAIN_STEP):
    SUM_BGD = 0
    for index in range(len(X_INPUT)):
        SUM_BGD += (train_func(X_INPUT[index], k_BGD) - Y_OUTPUT_CORRECT[index]) * X_INPUT[index]# 所有样本
    k_BGD -= LEARNING_RATE * SUM_BGD
    k_BGD_RECORD.append(k_BGD)

# SGD
k_SGD = 0.0
k_SGD_RECORD = []
for step in range(TRAIN_STEP):
    index = np.random.randint(len(X_INPUT))
    SUM_SGD = (train_func(X_INPUT[index], k_SGD) - Y_OUTPUT_CORRECT[index]) * X_INPUT[index]# 一个样本
    k_SGD -= LEARNING_RATE * SUM_SGD
    k_SGD_RECORD.append(k_SGD)

# MBGD
k_MBGD = 0.0
k_MBGD_RECORD = []
for step in range(TRAIN_STEP):
    SUM_MBGD = 0
    index_start = np.random.randint(len(X_INPUT) - BATCH_SIZE)
    for index in np.arange(index_start, index_start+BATCH_SIZE):
        SUM_MBGD += (train_func(X_INPUT[index], k_MBGD) - Y_OUTPUT_CORRECT[index]) * X_INPUT[index]# batch_size个样本
    k_MBGD -= LEARNING_RATE * SUM_MBGD
    k_MBGD_RECORD.append(k_MBGD)

# 作图
plt.plot(np.arange(TRAIN_STEP), np.array(k_BGD_RECORD), label='BGD')
plt.plot(np.arange(TRAIN_STEP), k_SGD_RECORD, label='SGD')
plt.plot(np.arange(TRAIN_STEP), k_MBGD_RECORD, label='MBGD')
plt.legend()
plt.ylabel('weight')
plt.xlabel('step')
plt.show()

——代码来源：梯度下降（BGD、SGD、MSGD）差异

---

5.2 tensorflow应用：

import tensorflow as tf
 
# Model parameters
W = tf.Variable([.3], dtype=tf.float32)
b = tf.Variable([-.3], dtype=tf.float32)
# Model input and output
x = tf.placeholder(tf.float32)
linear_model = W*x + b
y = tf.placeholder(tf.float32)
 
# loss
loss = tf.reduce_sum(tf.square(linear_model - y)) # sum of the squares
# optimizer
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)
 
# training data
x_train = [1, 2, 3, 4]
y_train = [0, -1, -2, -3]
# training loop
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init) # reset values to wrong
for i in range(1000):
  sess.run(train, {x: x_train, y: y_train})
 
# evaluate training accuracy
curr_W, curr_b, curr_loss = sess.run([W, b, loss], {x: x_train, y: y_train})
print("W: %s b: %s loss: %s"%(curr_W, curr_b, curr_loss))

——代码参考：tensorflow-梯度下降,有这一篇就足够了

6. 梯度下降法和其他无约束优化算法的比较：

在机器学习中的无约束优化算法，除了梯度下降以外，还有前面提到的最小二乘法，此外还有牛顿法和拟牛顿法。

梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。

梯度下降法和牛顿法/拟牛顿法相比，两者都是迭代求解，不过梯度下降法是梯度求解，而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言，使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。

参考：梯度下降（Gradient Descent）小结

7. BGD、SGD、MBGD总结：

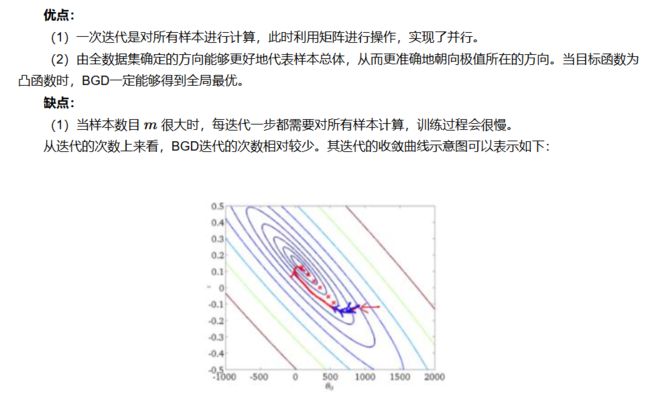
7.1 BGD：

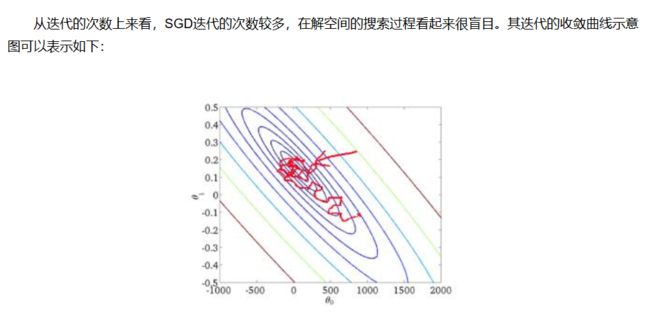
7.2 SGD：

7.3 MBGD：

7.4 为什么SGD收敛速度比BGD要快？

这里我们假设有个样本，对于BGD而言，每次迭代需要计算个样本才能对参数进行一次更新，需要求得最小值可能需要多次迭代（假设这里是）；而对于SGD，每次更新参数只需要一个样本，因此若使用这个样本进行参数更新，则参数会被更新（迭代）次，而这期间，SGD就能保证能够收敛到一个合适的最小值上了。也就是说，在收敛时，BGD计算了次，而SGD只计算了次。

——参考：批量梯度下降(BGD)、随机梯度下降(SGD)以及小批量梯度下降(MBGD)的理解

---

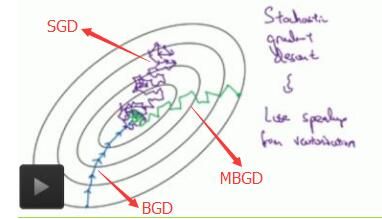
最后，附上一张总结图（这无人能敌的字迹，逃~）

写在最后：

资料参考：

• 梯度下降（Gradient Descent）小结
• 梯度下降（BGD、SGD、MSGD）差异
• 批量梯度下降(BGD)、随机梯度下降(SGD)以及小批量梯度下降(MBGD)的理解
• tensorflow-梯度下降,有这一篇就足够了

学无止境！！！