我的理解,haskell创造了一个no side-effect的pure functional的world,然后为了和real world协同,创造了monad来封装real world中的dirty data。
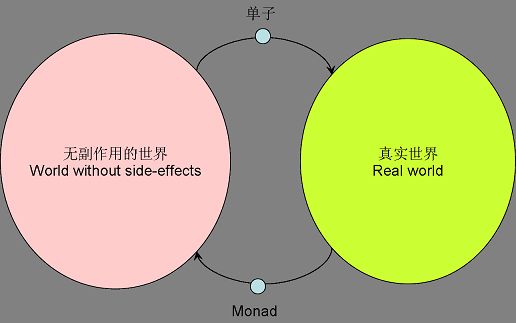
图1 左边是无副作用世界,右边是真实世界,二者通过交换单子进行协同当real world中发生一个destructive update的时候(输入),它把这个update一刻的瞬间snapshot下来,产生一个monad;这个monad随即被送往no side-effect world(下简称pure world)。
pure world从单子中取出数据,进行运算,这个过程是pure的。处理完成后,它把结果封装成一个新的单子返回给真实世界,真实世界再发生一次destructive update(输出)。
一个Monad m定义了一个运算(computation):
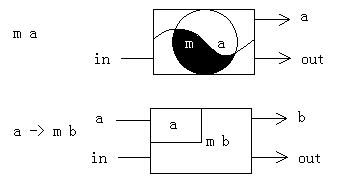
图中上面一个是monad m a,下面一个是function (a->m b)。
可以大致这么理解,一个monad是包含两面的,它除了在一个世界中作为a以外,还携带了另外一个世界如何从in变化到out的信息。所以,一个monad还叫做action,或者computation。例如,IO monad又称IO action。后面为了不用每次画图,我们这样画一个monad:
a//in->out,或者a//in,或者a//out
而a->m b这样画:
a->b//in->out
Monad有四个基本运算分别是:bind(>>=), then(>>), return, fail。
从数学的角度讲,一个monad只需要两个运算,>>=和return就够了。不过从程序设计角度,为了便利,添加了>>和fail,他们分别是>>=和return的特化型。
bind运算把一个monad m a的pure部分取出来,放到一个monad constructor (a->m b)中,构造器产生一个新的monad m b,借此把a输送给real world。
then运算是特殊的bind,它描述了两个monad的顺序诞生。
return运算是一个特殊的constructor,它接受一个pure world中的a,产生一个monad m a。
fail运算是特殊的return,它接受一个String之后,产生一个monad,同时把这个String输送给real world。
monad三定律:
(1) return a >>= k == k a
(2) m >>= return == m
(3) m >>= (/x -> k x >>= h) == (m >>= k) >>= h
第一个,monad bind到constructor等价于直接apply monad中的pure部分到constructor。
第二个,return保留monad的所有信息不变。
第三个,bind运算满足结合律。
好了,看了这么些难以理解的概念之后,让我们看看几个实际的例子吧。
putStrLn :: String -> IO ()
putStrLn函数根据pure world中的一个String构造了一个IO monad IO ()。Just :: a -> Maybe a
Just这个constructor根据a构造一个Maybe monad Maybe a。
试试把一个Maybe monad bind到print看看:
Prelude> (Just 3)>>=print
Couldn't match expected typeMaybe' against inferred typeIO'
Expected type: t -> Maybe b
Inferred type: t -> IO ()
看起来,monad只能bind到能够构造同类型monad的constructor上。
Prelude> let f x | x>=0 = Just (x+1) | x<0 = Nothing
Prelude> :t ff :: (Ord a, Num a) => a -> Maybe a
Prelude> (Just 3)>>=f
Just 4
Prelude> (Just (-1))>>=f
Nothing
进一步看看:
Prelude> :t f 3
f 3 :: (Ord t, Num t) => Maybe t
Prelude> :t f (-1)
f (-1) :: (Ord a, Num a) => Maybe a
可以看到,real world中不是只有I/O一种action。rollDice = getStdRandom (randomR (1,6)) :: IO Integer
这是一个随机数产生函数。
试试看:
Prelude> :m System.Random
Prelude System.Random> let rollDice = getStdRandom(randomR(1,6))
Prelude System.Random> mapM (/x->rollDice) [1..12]
[3,5,3,6,2,4,5,1,5,6,3,2]
为什么monad的引入就能够把pure world和real world和谐的结合起来呢?
rollDice函数不是不符合“给出相同的参数,返回相同的结果”么?
我们先来看看pure function的定义吧:
wikipedia上是这么写的:
In computer programming, a function may be described as pure if both these statements about the function hold.
- The function always evaluates the same result value given the same argument value(s). The function result value cannot depend on any hidden information or state that may change as program execution proceeds, nor can it depend on any external input from IO devices.
- Evaluation of the result does not cause any semantically observable side effect or output, such as mutation of mutable objects or output to IO devices.
翻译一下就是:
- 给出相同的参数,函数总是求值出相同的结果。结果不能依赖于任何在程序运行过程中可能改变的隐含的信息或者状态,也不能依赖于任何外部输入例如IO设备。
- 对结果的求值不能导致任何语义上可以观察到的副作用或者输出,例如可变对象的改变或者IO设备上的输出。
结论是显然的但又是令人困惑的,rollDice不是pure的?!
但是haskell作为一个pure functional语言是不允许定义impure的function的。
矛盾!?
其实,因为有了monad和lazy evaluation,这个矛盾便得以调和。
还记得rollDice的类型吧:rollDice :: IO Integer//rand(1,6)
你说它是一个monad也好,说它是一个制造monad的函数也好,请记住,函数是一类公民!
好,注意这里,我们并不需要rollDice的结果,因为现在用不到。
然后,我们把它放到了一个mapM里面去运算:
mapM (/x->rollDice) [1..12]
用rollDice构造出来的函数(/x->rollDice)是:t->IO Integer//rand(1,6)
看看mapM是干什么的吧: mapM :: (Monad m) => (a -> m b) -> [a] -> m [b]好啦,mapM由[1..12]得到了一个新的monad IO [Integer]//rand(1,6) repeat 12
我们还是不需要求值。
现在,该把这个monad从pure world扔到real world了,我们使用print :: a -> IO ()
(mapM (/x->rollDice) [1..12])>>=print
monad IO [Integer]把它的[Integer]部分交给了print,bind之后得到了一个新的monad IO ()//print rand(1,6) repeat 12 to stdout
real world不是lazy的,它计算了12次rand(1,6),然后把它们打印到了终端上,于是我们的终端上立刻显示出了诸如[6,6,2,6,5,3,1,3,6,4,2,5]之类的数列。
回过头来看一看,rollDice、mapM、print之类的函数是pure function吗?
答案是——yes!
在pure world,函数是lazy的。rollDice每次调用都会返回IO rand(1,6),在纯函数世界里,这不过就是一个名字"rand(1,6)"而已;而这个monad却同时定义了真实世界里的一个计算,那就是计算1~6之间的一个随机数。当把这个monad从pure world扔到real world之后,real world便进行强制求值,于是就得到了一个随机数。
lazy要call by name,计算name,返回name。strict要call by value,计算value,返回value。这就是haskell的纯函数世界和真实世界最大的不同。
Haskell de facto describes a quantum world.
-- St. Monad
先讲一个故事吧,薛定谔的猫(Schrodinger's cat)的故事。这是关于量子理论的一个理想实验。
这个猫十分可怜,她(假设这是一只雌性的猫,以引起更多怜悯)被封在一个密室里,密室里有食物有毒药。毒药瓶上有一个锤子,锤子由一个电子开关控制,电子开关由放射性原子控制。如果原子核衰变,则放出阿尔法粒子,触动电子开关,锤子落下,砸碎毒药瓶,释放出里面的氰化物气体,雌猫必死无疑。这个残忍的装置由薛定谔所设计,所以雌猫便叫做薛定谔猫。原子核的衰变是随机事件,物理学家所能精确知道的只是半衰期——衰变一半所需要的时间。如果一种放射性元素的半衰期是一天,则过一天,该元素就少了一半,再过一天,就少了剩下的一半。但是,物理学家却无法知道,它在什么时候衰变,上午,还是下午。当然,物理学家知道它在上午或下午衰变的几率——也就是雌猫在上午或者下午死亡的几率。如果我们不揭开密室的盖子,根据我们在日常生活中的经验,可以认定,雌猫或者死,或者活。这是她的两种本征态。但是,如果我们用薛定谔方程来描述薛定谔猫,则只能说,她处于一种活与不活的叠加态。我们只有在揭开盖子的一瞬间,才能确切地知道雌猫是死是活。此时,猫的波函数由叠加态立即收缩到某一个本征态。量子理论认为:如果没有揭开盖子,进行观察,我们永远也不知道雌猫是死是活,她将永远到处于半死不活的叠加态。这与我们的日常经验严重相违,要么死,要么活,怎么可能不死不活,半死半活?
薛定谔挖苦说:按照量子力学的解释,箱中之猫处于“死-活叠加态”——既死了又活着!要等到打开箱子看猫一眼才决定其生死。(请注意!不是发现而是决定,仅仅看一眼就足以致命!)正像哈姆雷特王子所说:“是死,还是活,这可真是一个问题。”只有当你打开盒子的时候,迭加态突然结束(在数学术语就是“坍缩(collapse)”),哈姆雷特王子的犹豫才终于结束,我们知道了猫的确定态:死,或者活。哥本哈根的几率诠释的优点是:只出现一个结果,这与我们观测到的结果相符合。但是有一个大的问题:它要求波函数突然坍缩。但物理学中没有一个公式能够描述这种坍缩。尽管如此,长期以来物理学家们出于实用主义的考虑,还是接受了哥本哈根的诠释。付出的代价是:违反了薛定谔方程。这就难怪薛定谔一直耿耿于怀了。
哥本哈根诠释在很长的一段时间成了“正统的”、“标准的”诠释。但那只不死不活的猫却总是像恶梦一样让物理学家们不得安宁。格利宾在《寻找薛定谔的猫》中想告诉我们的是,哥本哈根诠释在哪儿失败,以及用什么诠释可以替代它。
1957年,埃弗雷特提出的“多世界诠释”似乎为人们带来了福音,虽然由于它太离奇开始没有人认真对待。格利宾认为,多世界诠释有许多优点,由此它可以代替哥本哈根诠释。我们下面简单介绍一下埃弗雷特的多世界诠释。
格利宾在书中写道:“埃弗雷特……指出两只猫都是真实的。有一只活猫,有一只死猫,但它们位于不同的世界中。问题并不在于盒子中的放射性原子是否衰变,而在于它既衰变又不衰变。当我们向盒子里看时,整个世界分裂成它自己的两个版本。这两个版本在其余的各个方面都是全同的。唯一的区别在于其中一个版本中,原子衰变了,猫死了;而在另一个版本中,原子没有衰变,猫还活着。”
也就是说,上面说的“原子衰变了,猫死了;原子没有衰变,猫还活着”这两个世界将完全相互独立地演变下去,就像两个平行的世界一样。格利宾显然十分赞赏这一诠释,所以他接着说:“这听起来就像科幻小说,然而……它是基于无懈可击的数学方程,基于量子力学朴实的、自洽的、符合逻辑的结果。”“在量子的多世界中,我们通过参与而选择出自己的道路。在我们生活的这个世界上,没有隐变量,上帝不会掷骰子,一切都是真实的。”按格利宾所说,爱因斯坦如果还活着,他也许会同意并大大地赞扬这一个“没有隐变量,上帝不会掷骰子”的理论。
这个诠释的优点是:薛定谔方程始终成立,波函数从不坍缩,由此它简化了基本理论。它的问题是:设想过于离奇,付出的代价是这些平行的世界全都是同样真实的。这就难怪有人说:“在科学史上,多世界诠释无疑是目前所提出的最大胆、最野心勃勃的理论。”
读过大学物理的人大概都能够想起来这个故事。
haskell里的monad就好像故事里的这只小猫:当它在pure functional的世界被构造出来之后,尚未进入真实世界的时候,它就仿佛处于一个“波函数叠加”的状态,当其一进入真实世界——也就是被我们所“观察”的时候——“波函数”就坍塌了,“生死得以确知”——副作用得以发生。
拿之前所举的随机数的函数rollDice来说,其中的rand(1,6)在我们还没有“观察”它的时候,它既不是1,也不是2,也不是3,也不是4,也不是5,也不是6,它其实是以在1~6都可能的概率存在——描述这个概率的“波函数”是确定的,所以之前我说,rollDice :: IO Integer//rand(1,6)是pure function。为什么?因为rand(1,6)是一个“波函数”,这个“波函数”是确定的,所以rollDice函数每次都会返回同一个“波函数”,而这个“波函数”此刻并未被求值,因此说rollDice是完全符合pure function的定义的。
“波函数”就是monad对真实世界的描述,它用确知的方程式描述不确知的真实世界。
一切为了和谐。
ps, 巧的是,还真有人用平行世界的观点来诠释haskell的世界观,看来也是不希望薛定谔方程被违背的人呀!哈哈。
2007.04.02旧作,原发于CSDN blog http://blog.csdn.net/st_monad/article/details/1548862