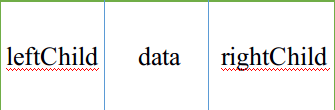二叉树的性质
性质1:
在二叉树的第i层上至多有2^(i-1)个结点(i>0)
因为一个节点度不大于2(即每个结点只能有两棵子树),如果假设这棵二叉树是一棵满二叉树,那么每个结点都有两棵子树,按每层来看的话,会发现它是首项为1,公比为2的等比数列,所以第i层最多有2^(i-1)个结点(i>0)
性质2:
一棵深度为k的二叉树中,最多有2^k-1个结点
其实这也很好得出这个性质,既然每层的结点数量就是等比数列的一项,那么深度为k的树,假设为满二叉树,那么结点总数就是等比数列求和,所以,一棵深度为k的二叉树中,最多有2^k-1个结点
性质3:
具有n个结点的完全二叉树的深度k为[log2n]+1
其实就是性质2的逆推,假设有棵深度为x的完全二叉树,那么他的结点总数的范围为2^(k-1)-1 < n <= 2^k-1,两边同时取对数得k-1 < og2n <= k,具有n个结点的完全二叉树的深度k为[log2n]+1
性质4:
对于一棵非空的二叉树,如果叶子结点数为n0,度为2的结点数为n2,
则n0 = n2+1
整棵树的结点数: n = n0+n1+n2 (n0叶子结点数,n1度为1的结点数,n2度为2的结点数)
根据节点度的定义子结点的的数量为: n0×0+n1×1+n2×2
子节点的数量为:n-1 (除根以外每个结点都是子节点)
所以解得 n0 = n2+1
性质5:
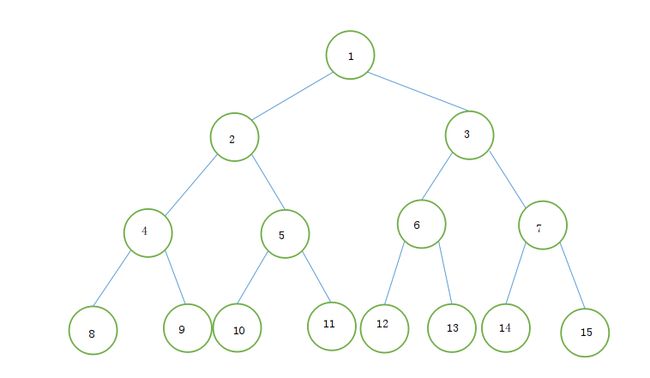
对于具有n个节点的完全二叉树,如果按照从上至下和从左至右的顺序对二叉树中所有结点进行从1的编号,则对于任意的序号为i结点,有:
- 如果i>1,则序号为i的结点的双亲结点为i/2,如果i==1,则序号为i的结点是根节点,无双亲结点
- 如果2i<=n,则序号为i的结点的左孩子节点的序号为2i,否则i结点无左孩子
- 如果2i+1<=n,则序号为i的结点的右孩子节点的序号为2i,否则i结点无右孩子
注意:性质1,2,4所有二叉树都通用,性质3,5只有完全二叉树适用
二叉树的存储结构
二叉树的存储方式也可以分为顺序存储结构和链式存储结构两种存储结构
二叉树的顺序存储结构
这里的顺序存储也是用一组连续的存储单元依次从上至下,从左至右存储二叉树上的节点元素。对于完全二叉树来说树中结点的序号都是按照从上至下,从左至右进行编排的,所以结点的序号可以唯一的反映节点之间的逻辑关系(性质5)
存储在数组中,数组下表从零开始
数组下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8
-------|----------------------------------
数据 | A | B | C | D | E | F | G | H | I
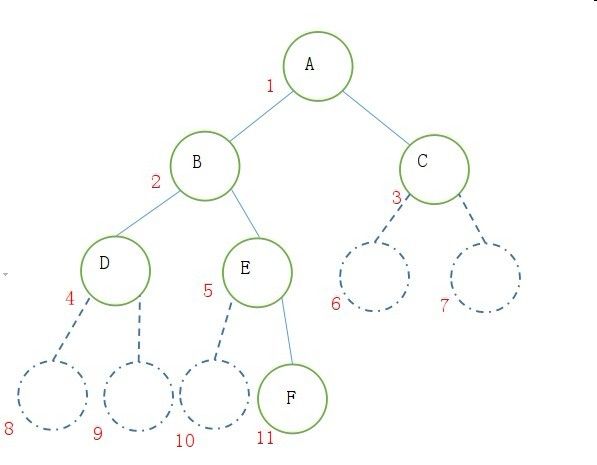
如果是一般的二叉树的话,如果我在对他进行从上至下,从左至右进行编号时就不能很好的反映数组元素之间的关系了,如果我们进行适当的改造,通过添加一些结点,把他补成一颗完全二叉树,那么再进行编号,就可以进行顺序存储了
数组下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10
-------|--------------------------------------------
数据 | A | B | C | D | E | 0 | 0 | 0 | 0 | 0 | F
由此可以看出,这样的存储方式,会造成很多空间的浪费,而且如果要进行对树上元素进行删除、插入操作需要移动大量的数据元素,因此二叉树不宜采用顺序存储结构
二叉树的链式存储结构
二叉树的链式存储结构就是,用类似于链表的存储方法来存储树上元素的逻辑关系,即用指针来表示元素之间的逻辑关系
data是数据域,leftChild和rightChild是指针域,leftChild是
指向左儿子的指针,rightChild是指向有儿子的指针,当左儿子或右儿子为空时,相应的指针域也为空
代码描述
//存储的数据类型
typedef char DataType
typedef struct node
{
DataType data; //数据域
struct node* leftChild; //左儿子
struct node* rightChild; //右儿子
}BinNode;
typedef BinNode* BinTree;
这是二叉链表的定义,除此之外还有三叉链表,三叉链表比起二叉链表多了一个指向双亲结点的指针域,如图所示
代码描述
//存储的数据类型
typedef char DataType
typedef struct node
{
DataType data; //数据域
struct node* leftChild; //左儿子
struct node* rightChild; //右儿子
struct node* parent; //双亲
}BinNode;
typedef BinNode* BinTree;