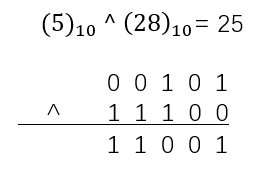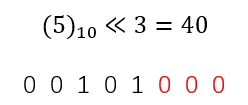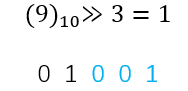开放下载:下载地址
注:未经允许不得进行转载、参考,本文归属权为作者所有,如有需求请先联系作者申请。
浅谈状压DP
作者:筱柒_Littleseven
地址:http://littleseven.top/
QQ/微信:3364445435 / yuqihao2003
目录
- 一、位运算及状压DP中常用的位运算技巧
- 二、状压DP概念及涉及到的一些铺垫知识
- 三、经典状压DP和简单例题
- 四、TSP(旅行商)问题的状压DP解法
- 五、状压DP的衍生
- 六、总结
一、位运算及状压DP中常用的位运算技巧
简单位运算介绍
运算符号:[PS.其中按位取反操作应用较少]
| 含义 | 表达式(Pascal语言) | C/C++语言 |
|---|---|---|
| 按位与 | a and b | a & b |
| 按位或 | a or b | a | b |
| 按位异或 | a xor b | a ^ b |
| 按位取反 | not a | ~ a |
| 左移 | a shi b | a << b |
| 右移 | a shr b | a >>b |
1. and(&)运算 按位与运算
在二进制下,相同位的数字都为 \(1\) ,则为 \(1\) ;若有一个不为 \(1\) ,则为 \(0\) 。
2. or(|)运算 按位或运算
在二进制下,相同位的数字只要一个为 \(1\) ,即为 \(1\) ;反之,则为 \(0\) 。
3. xor(^)运算 按位异或运算
在二进制下,相同位的数字相同则为 \(0\) ,不同则为 \(1\) 。也可以理解 \(Xor\) 运算为不进位的二进制加法运算。
4. not(~)运算 按位取反运算
在二进制下,把内存当中的 \(0\) 和 \(1\) 全部取反。这里要注意整数是否有符号等等。
5. shi(<<)运算 左移运算
在二进制下,把所有位数字向左移动,并在后边补上 \(0\) 。
6. shr(>>)运算 右移运算
在二进制下,把所有数字向右移动,并去掉末尾位数。
常用位运算技巧
- 取出二进制数 \(x\) 的第 \(k\) 位:
y = 1 << k & x或y = x >> k & 1 - 取出二进制数 \(x\) 的最后一个 \(1\) (\(lowbit\)):
y = x & (-x) - 将二进制数 \(x\) 的第 \(k\) 位变成 \(1\) :
x = x | (1 << k) - 将二进制数 \(x\) 的第 \(k\) 位变成 \(0\) :
x = x & (~ (1 << k)) - 将二进制数 \(x\) 的第 \(k\) 位取反:
x = x ^ (1 << k) - 取出二进制数 \(x\) 的最后 \(k\) 位:
y = x & ((1 << k) - 1)
位运算优先级
| 优先级 | 运算符(C/C++) |
|---|---|
| 1 | ~ |
| 2 | <<,>> |
| 3 | & |
| 4 | ^ |
| 5 | | |
| 6 | &=,^=,|=,<<=,>>= |
二、状压DP概念及涉及到的一些铺垫知识
状压DP
状压 dp 是动态规划的一种,通过将状态压缩为整数来达到优化转移的目的。 [——来自 OI Wiki]
对于概念的一些补充解释
状态压缩,指的是我们需要将动态规划的一部分状态压缩起来处理。这些状态应该保证一定的相似性、状态的可能性许多、适合集中处理且便于压缩处理。
动态规划是解决多阶段决策最优化问题的一种方法,状压优化也不能对此有影响。所以由此来看,状压DP只是动态规划的一种优化方法,或者说是一种实现方法,并没有改变动态规划的本质。
而对于较简单且常见的状压DP,实现的方式通常是将一行的决策情况(状态)压成一个数。而这一个数所有二进制位,则代表这一行的情况,这似乎与部分题当中的 \(bitset\) 有异曲同工之妙。而在这个实现过程中就需要很多涉及位运算的问题。这样更体现出状压DP适合解决选不选的问题,将一个 \(bool\) 数组变成一个 \(int\) 。并且状压DP不适合情况数过多的情况,假如我们在这一行中有 \(60\) 个点,那么我们在状态的这一维需要开一个 \(2^{60}\) 的数组,显然这不太现实。
并且对于动态规划来说,需要保证无后效性和最优子结构两个性质,特别是无后效性限制了这个DP的状态与实现方式。在状压DP中当然是也要保证这两个最基本的性质,所以状态压缩的状态、压缩状态的方式、状态转移的实现方式对于保证这个DP的正确性来说都是至关重要的。
对于状压DP的例子
问题:
有 \(n\) 件物品和一个容量为 \(v\) 的背包。放入第 \(i\) 件物品会占用 \(c_i\) 的空间,同时也会得到 \(w_i\) 的价值。求解对于每种方法这个背包的价值。
分析:
- 状态:
- 由于问题是每一种背包的价值。显然我们需要拿到每一种背包的放置情况,那么不妨就设状态是:对于这 \(n\) 件物品放与不放的情况,答案是多少。
- 这时我们会发现,如果开一个 \(n\) 维数组,第 \(i\) 维用 \(0/1\) 表示这个物品选还是不选,这样的话这个问题将会迎刃而解。但是显然空间不允许我们这种做法,同样很难实现这个 \(n\) 维数组。所以我们考虑状压。
- 如果当前有 \(8\) 个物品(\(n = 8\)),根据多维数组我们要开一个 \(f[s][s][s][s][s][s][s][s]\) 数组(其中 \(s\) 代表 $0/1 $)。由于每种物品只有选或者不选两种情况,那么我们考虑把这 \(8\) 个维度压在一起变成 \(f[0000000]\sim f[11111111]\) 这么一个数组。这样我们只需要开一个 \(f[256]\) 就可以了。
- 转移:
- 由于对于一个物品,放的状态能且仅能从不放的状态转移而来。对于 \(f[10000]~~(f[16])\) 则从 \(f[00000]~~(f[0])+w[1]\) 转移而来;而对于 \(f[11000]~~(f[24])\) 则可以由 \(f[10000]~~(f[26])+w[2]\) 转移而来,也可以由 \(f[01000]~~(f[8])+w[1]\) 转移而来。
- 答案
- \(f[S]\) 则表示在状态 \(S\) 下这个背包的价值。
状压DP的特点
- DP规模较小(\(n<= 20\)),适合多维压缩计算,并且被压缩的维度的性质应相似。
- 一般情况下只有两种决策(也可能会有多种出现)。
三、经典状压DP和简单例题
洛谷 P1879 [USACO06NOV]玉米田Corn Fields
题目链接
题目大意:
现在又一个 \(n \times m\) 的牧场,对于每一个格子,有的可以种上牧草,有的则不能。但是无论如何不可以选择相邻的两块草地种植牧草,也就是任意的两块草地都没有公共边。现在想知道一共可以有多少种种植方案(不种植牧草也是一种方案)。(\(1\le n,m \le 12\))
分析:
通过这道题的数据范围我们会发现,每一块草地只有种或不种的两种决策,并且对于每一块草地都是相同性质的决策。同样这个范围是可以压缩的 \(2^{12} = 4096\) 。
所以我们把每一行的状态压在一个状态当中。例如 \(00000\) 表示这一行不种牧草,而 \(00100\) 表示在这一行的第三个位置种牧草。
之后考虑DP过程:
状态:我们设 \(f[i][s]\) 表示当前处理到第 \(i\) 行,在这行的状态为 \(s\) 的情况下的方案数。
转移:
这道题的转移其实很值得推敲。首先我们会明确其中有一些格子是本身就不能种植,而有一些格子是因为有相邻的格子种植了而不能种植。所以对于一个状态的合法性(也就是转移过程的条件)是要从很多方面进行考虑的。
- 首先我们考虑对于这个格子本质就不能种草的情况,我们可以在读入的时候直接把每一行压成一个状态,这样相当于直接拿出来了把这一行种满的情况(暂时不考虑相邻),这个状态中 \(1\) 的位置则表示这个位置可种, \(0\) 的位置则表示这个位置不可种。那么显然如果满足
j & s[i] == j,那么这个状态就是合法的。 - 其次我们来考虑横向相邻格子的情况,我们可以对于每一个状态进行一下预处理。通过
! i & (i << 1)来判断是否和右边草地相连,通过! i & (i >> 1)判断是否和左边草地相连。 - 再来考虑纵向相邻格子的情况,在转移的过程中,我们可以找到所有与当前 \(f[i][s]\) 没有纵向相邻方格的 \(f[i - 1][k]\) 进行转移。这时候需要保证
k & j == 0,即两行之间没有纵向的相邻格子。
- 首先我们考虑对于这个格子本质就不能种草的情况,我们可以在读入的时候直接把每一行压成一个状态,这样相当于直接拿出来了把这一行种满的情况(暂时不考虑相邻),这个状态中 \(1\) 的位置则表示这个位置可种, \(0\) 的位置则表示这个位置不可种。那么显然如果满足
答案:由于并不知道最后的答案是在什么,也没有具体的答案。对于这道题,他的答案就是 $\sum_{i=1}^n f[n][i] $。
AC代码:
#include
using namespace std;
const int N = 15;
const int S = (1 << 12) + 10;
const int mod = 1e8;
int n, m, mp[N][N];
bool is[S]; // 判断当前状态是否合法
int s[N], f[N][S]; // s[]存放每一行的初始状态,f[][]是DP数组
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) {
for (int j = 1; j <= m; j ++ ) {
scanf("%d", &mp[i][j]);
s[i] = (s[i] << 1) | mp[i][j];
// 更新每一行的初始状态
}
}
for (int i = 0; i <= (1 << m) - 1; i ++ ) {
if ((! (i & (i << 1))) && (! (i & (i >> 1)))) {
is[i] = 1;
// 判断一个状态是否合法
// ! (i & (i << 1)) 判断是否和右边草地相连
// ! (i & (i >> 1)) 判断是否和左边草地相连
}
}
f[0][0] = 1; // 初值,表示在第 0 行选出来 0 个位置的方案数
for (int i = 1; i <= n; i ++ ) { // 枚举当前是第i行
for (int j = 0; j <= (1 << m) - 1; j ++ ) { // 枚举状态
if (is[j] && (j & s[i]) == j) { // 当前状态合法,并且也符合这一行的地形
for (int k = 0; k <= (1 << m) - 1; k ++ ) { // 枚举上一行的状态
if ((k & j) == 0) { // 如果上一行和这一行没有在纵向方向上相邻的
f[i][j] = ((f[i][j] + f[i - 1][k])) % mod; // 记录答案
}
}
}
}
}
int ans = 0;
for (int i = 0; i <= (1 << m) - 1; i ++ ) {
ans = (ans + f[n][i]) % mod; // 循环统计方案数
}
printf("%d\n", ans);
return 0;
}
洛谷 P1896 [SCOI2005]互不侵犯 BZOJ 1087: [SCOI2005]互不侵犯King
题目链接
题目大意:
在 \(N\times N\) 的棋盘里面放K个国王,使他们互不攻击,共有多少种摆放方案。国王能攻击到它上下左右,以及左上
左下右上右下八个方向上附近的各一个格子,共 \(8\) 个格子。
分析:
首先这道题看起来和上道题有一些相似处,那么我们对比一下这两道题:
- 第一题只限制了四个方向,而这道题是限制了八个方向
- 第一题中只有方向上的限制,而这道题有人数上的限制
对于上一道题,我们需要开一个二维的数组来实现DP的过程,\(f[i][s]\) 表示到 \(i\) 行且第 \(i\) 行的状态为 \(s\) 的方案数。而显然对于这道题,人数的限制十分令人头疼,我们不得不用三维数组 \(f[i][s][k]\) ,虽然数组开的下(开不下可以优化),但是这道题当中的人数和方案数有关联,或者说一种当前行状态会对应当前状态下一个特定的人数。
而解决方案则是选择使用DFS来找到所有合法的情况,单独使用 \(s[]\) 数组存每个合法状态的状态, \(num[]\) 存达到这个状态需要这一行放多少个国王。
void dfs(int pos, int ss, int tot) {
if (pos >= n) {
s[ ++ cnt] = ss;
num[cnt] = tot;
return ;
}
dfs(pos + 1, ss, tot);
dfs(pos + 2, ss + (1 << pos), tot + 1);
} 这个时候在考虑整个DP的情况:
- 状态:\(dp[i][j][k]\) 表示当前处理到第 \(i\) 行,在这一行选择编号为 \(j\) 的摆放方案,在当前的状态下已经选择了 \(k\) 个国王的方案数。
- 转移:
- 对于同一行之间国王的冲突,在在于处理的过程中直接避免
- 对于上下两行之间国王的冲突,
if(s[j] & s[k]) continue; - 对于左上方和右下方之间国王的冲突,
if(s[j] & (s[k] >> 1)) continue ; - 对于右上方和左下方之间国王的冲突,
if(s[j] & (s[k] << 1)) continue ; - 最终按照背包过程进行转移即可
AC代码:
#include
using namespace std;
typedef long long ll;
const int N = 12;
const int S = 2010;
int n, m;
int cnt, s[N * N], num[N * N];
// cnt计数,s数组存状态,num数组存达到当前状态需要用多少个国王。
ll dp[N][S][N * N];
void dfs(int pos, int ss, int tot) {
// DFS预处理出所有的状态
// 由于在这道题需要统计国王的数量,所以一个状态是存不下的,而且状态又与国王的数量有关,所以采用这种方式
if (pos >= n) {
s[ ++ cnt] = ss;
num[cnt] = tot;
return ;
// 当pos>=n的时候说明已经找到一个满足一行的状态了
}
dfs(pos + 1, ss, tot);
dfs(pos + 2, ss + (1 << pos), tot + 1);
}
int main() {
scanf("%d%d", &n, &m);
dfs(0, 0, 0);
for (int i = 1; i <= cnt; i ++ ) {
dp[1][i][num[i]] = 1ll;
}
// 预处理出来所有第一行的答案都=1
for (int i = 2; i <= n; i ++ ) { // 枚举行数
for (int j = 1; j <= cnt; j ++ ) { // 枚举当前方案
for (int k = 1; k <= cnt; k ++ ) { // 枚举上一行方案
if (s[j] & s[k]) {
// 这里说明这一行存在某个国王在上一行的下边
continue ;
}
if (s[j] & (s[k] >> 1)) {
// 这里说明这一行存在某个国王在上一行的右下角
continue ;
}
if (s[j] & (s[k] << 1)) {
// 这里说明这一行存在某个国王在上一行的左下角
continue ;
}
for (int l = num[j]; l <= m; l ++ ) {
dp[i][j][l] += dp[i - 1][k][l - num[j]];
}
}
}
}
ll ans = 0;
for (int i = 1; i <= cnt; i ++ ) {
ans += dp[n][i][m];
}
printf("%lld\n", ans);
return 0;
} 洛谷 P2704 [NOI2001]炮兵阵地
题目链接
题目大意:
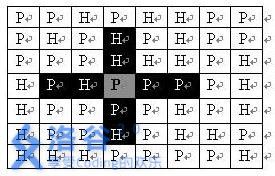
司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。一个NM的地图由N行M列组成,地图的每一格可能是山地(用“H” 表示),也可能是平原(用“P”表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
分析:
我们会发现 \(m \le 10\) ,并且对于每一个位置只有放与不放的两种决策,并且是一道最优化,那么考虑状压DP 。
首先我们发现,这道题与前两题不同的就是前两道题是方案数,而这道题是最大值。而且前两道题当前一行的状态只和前一行有关,而显然这道题当中当前行的状态需要从前两行共同决定。
对于这个问题,我们采用以下DP:
- 状态:既然与两行都有关,不妨就把两个状态都枚举出来。设 $dp[i][j][k] $ 表示当前在第 \(i\) 行,当前行的状态为 \(j\) ,前一行的状态为 \(k\) 时最多可以排放的炮兵部队数量。
- 转移:这道题难点还是在于转移。首先我们发现第一行和第二行是必须预处理出来的。而从第三行开始,我们需要枚举当前行的状态,上一行的状态,上两行的状态。只有三个满足合法条件,才可以通过上边两个转移到当前这个。(在地图上是前两行转移到当前行,而在DP过程上是上一个DP状态转移到当前的DP状态,这里需要理解)
- 答案:答案显然就是 \(max(dp[i][j][k])~~~(1\le j \le cnt,~1\le k \le cnt)\)。
这道题属于状压DP非常经典的一道题,从这三道题当中应该可以发现状压DP的一些小规律。
AC代码:
#include
using namespace std;
const int N = 110;
const int M = 12;
char str[20];
int n, m, mp[N][M], ori[N];
// mp来存整个地图的山地还是平地的情况。
// ori来存每一行压缩后的状态 1为山地0为平地
int cnt, s[N * M], num[N * M];
// s来存每一个状态,num来存这个状态有多少个炮
int dp[N][(1 << 10)][(1 << 10)];
int getbit(int x) {
// 用来取出对于一个数 x 在二进制下一共有几个 1
int ret = 0;
while (x) {
ret ++ ;
x -= x & (-x);
}
return ret;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) {
scanf("%s", str + 1);
for (int j = 1; j <= m; j ++ ) {
if (str[j] == 'H') {
mp[i][j] = 1;
}
}
}
for (int i = 1; i <= n; i ++ ) {
for (int j = 1; j <= m; j ++) {
ori[i] = (ori[i] << 1) + mp[i][j];
}
}
s[ ++ cnt] = 0; // 由于一行什么都不放也是一种状态,所以s[1] = 0,num[1] = 0
for (int i = 1; i <= (1 << m) - 1; i ++ ) {
if (i & (i << 1)) { // 是否与右边第一个冲突
continue ;
}
if (i & (i << 2)) { // 是否与右边第二个冲突
continue ;
}
if (i & (i >> 1)) { // 是否与左边第一个冲突
continue ;
}
if (i & (i >> 2)) { // 是否与左边第二个冲突
continue ;
}
s[ ++ cnt] = i;
num[cnt] = getbit(i);
}
// 对于第一行预处理:
for (int i = 1; i <= cnt; i ++ ) {
if ((ori[1] & s[i]) == 0) {
dp[1][i][0] = num[i];
}
}
// 对于第二行预处理:
for (int i = 1; i <= cnt; i ++ ) {
if ((ori[2] & s[i]) == 0) {
for (int j = 1; j <= cnt; j ++ ) {
if (((s[i] & s[j]) == 0) && (((ori[1] & s[j]) == 0))) {
dp[2][i][j] = num[i] + num[j];
}
}
}
}
// DP过程:
for (int i = 3; i <= n; i ++ ) {
for (int j = 1; j <= cnt; j ++ ) {
if ((s[j] & ori[i]) == 0) {
for (int k1 = 1; k1 <= cnt; k1 ++ ) {
if (((s[k1] & ori[i - 1]) == 0) && (((s[k1] & s[j]) == 0))) {
for (int k2 = 1; k2 <= cnt; k2 ++ ) {
if (((ori[i - 2] & s[k2]) == 0) && ((s[k1] & s[k2]) == 0) && ((s[j] & s[k2]) == 0)) {
dp[i][j][k1] = max(dp[i][j][k1], dp[i - 1][k1][k2] + num[j]);
}
}
}
}
}
}
}
int ans = 0;
for (int i = 1; i <= cnt; i ++ ) {
for (int j = 1; j <= cnt; j ++ ) {
ans = max(ans, dp[n][i][j]);
}
}
printf("%d\n", ans);
return 0;
} 洛谷 P4460 [CQOI2018]解锁屏幕 BZOJ 5299: [Cqoi2018]解锁屏幕
题目链接
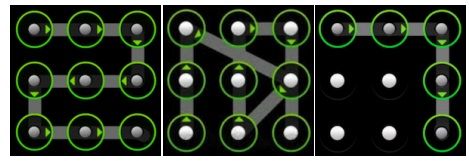
使用过Android手机的同学一定对手势解锁屏幕不陌生。Android的解锁屏幕由3x3个点组成,手指在屏幕上画一条线将其中一些点连接起来,即可构成一个解锁图案。如下面三个例子所示:
画线时还需要遵循一些规则
1.连接的点数不能少于4个。也就是说只连接两个点或者三个点会提示错误。
2.两个点之间的连线不能弯曲。
3.每个点只能"使用"一次,不可重复。这里的"使用"是指手指划过一个点,该点变绿。
4.两个点之间的连线不能"跨过"另一个点,除非那个点之前已经被"使用"过了。
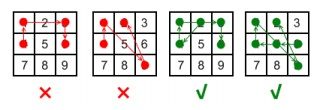
对于最后一条规则,参见下图的解释。左边两幅图违反了该规则:而右边两幅图(分别为2→4→1→3→6和→5→4→1→9→2)则没有违反规则,因为在"跨过"点时,点已经被"使用"过了。
现在工程师希望改进解锁屏幕,增减点的数目,并移动点的位置,不再是一个九宫格形状,但保持上述画线的规则不变。
请计算新的解锁屏幕上,一共有多少满足规则的画线方案。
分析:
这道题也算是和前边几个出现比较大差距的一道状压DP了。
我们会发现前几道题都是一个点和它周围 \(n\) 个点之间的限制,而这道题的限制似乎更广泛一些。而且前几道题都是对于网格图来说的,而这道题则是对于一些离散的点来说。
我们考虑一下限定条件:
- 点数 \(\ge 4\) 这个限定条件其实可以在最后统计时候进行判断。
- 不能弯曲,这个其实不用特殊处理,理解路径就行。
- 每个点只能使用一次,因为我们直接使用状态压缩,我们直接判一下当前点在当前状态中是否出现过即可。
- 连线不能跨过一个没走过的点。对于这个特殊的限定条件,我们需要在进行DP之前处理出对于 \(i\),\(j\) 两个点的连线上有那些点。这样可以选择用相似三角形判断共线或者使用斜率判断(较麻烦)。
之后考虑状态。首先我们既然选择把这 \(n\) 个点压成一维,我们就一定要从这里边的点向外边连线,而且我们又发现对于同一个状态,先走某个点和后走某个点并不算做同一种情况。这时我们发现,无论如何我们的状态中都要有当前状态和从状态中的哪个点向外引边。所以不妨就设状态为 \(f[s][i]\) 为当前所有点的 \(0/1\) 状态为 \(s\),最后一个点选择 \(i\) 的画线方案数。
转移则是每次枚举当前状态的一个点,向其他没有在当前状态的点引边,如果这条边合法则可以转移,不合法则跳过。
统计答案的时候特殊判一下当前这个答案是不是最少连接了 \(4\) 个点即可。
AC代码:
#include
using namespace std;
typedef long long ll;
const int mod = 1e8 + 7;
const int N = 21;
int n, Log[1 << N];
// Log[]便于直接取出当前这个元素在第几个位置(状态中的这个1代表的是第几个点)
int line[N][N];
// line[i][j] 存从i到j连线上的点,同样这里也将状态压缩成一个数
ll f[1 << N][N], ans;
struct Node {
int x, y;
} node[N];
void init() {
Log[1] = 0;
for (int i = 2; i <= (1 << n) - 1; i ++ ) {
Log[i] = Log[i >> 1] + 1;
}
// 预处理Log[]
}
bool check(Node xx, Node a, Node b) {
// 检验点xx是否在a->b的线段上
if (xx.x < min(a.x, b.x) || xx.x > max(a.x, b.x)) {
// 可能在直线上但是一定不在线段上
return 0;
}
if (xx.y < min(a.y, b.y) || xx.y > max(a.y, b.y)) {
// 可能在直线上但是一定不在线段上
return 0;
}
return ((a.x - xx.x) * (xx.y - b.y) == (xx.x - b.x) * (a.y - xx.y));
// 在线段上
}
int lowbit(int x) {
// lowbit函数(同树状数组中的lowbit),用来取出x在二进制下最右边一个1
return x & (-x);
}
int main() {
scanf("%d", &n);
init();
for (int i = 0; i < n; i ++ ) {
scanf("%d%d", &node[i].x, &node[i].y);
}
for (int i = 0; i < n; i ++ ) {
f[1 << i][i] = 1ll;
// 初值
}
for (int i = 0; i < n; i ++ ) {
for (int j = 0; j < n; j ++ ) {
for (int k = 0; k < n; k ++ ) {
if (k != i && k != j) {
if (check(node[k], node[i], node[j])) {
// 处理出对于每一条边经过了哪些点
line[i][j] |= (1 << k);
}
}
}
}
}
for (int s = 0; s <= (1 << n) - 1; s ++ ) {
for (int k = 0; k < n; k ++ ) {
int now = s;
while (now) {
int ss = lowbit(now);
int pos = Log[ss];
// 这里通过lowbit来实现枚举,比一位一位判断要更省时间
if ((! (s & (1 << k))) && ((line[pos][k] & s) == line[pos][k])) {
// 更新状态,判断是否出现过以及是否在当前这两个点的连线上有其他的点
f[s | (1 << k)][k] = (f[s | (1 << k)][k] + f[s][pos]) % mod;
}
now -= lowbit(now);
}
}
}
for (int s = 0; s <= (1 << n) - 1; s ++ ) {
int cnt = 0;
ll tmp = 0ll;
for (int i = 0; i < n; i ++ ) {
if (s & (1 << i)) {
// 记录点个数和答案
cnt ++ ;
tmp = (tmp + f[s][i]) % mod;
}
}
if (cnt >= 4) {
// 当个数>=4个的时候就更新答案
ans = (ans + tmp) % mod;
}
}
printf("%lld\n", ans);
return 0;
} 四、TSP(旅行商)问题的状压DP解法
TSP(旅行商)问题
注明:这里只是简单介绍,以便于对类似TSP问题的状压dp问题进行讨论。并且在这篇讲解当中涉及到的TSP问题都是简化的TSP问题,即并非每个城市只走一次或者路径可以重复等等
旅行商问题,即TSP问题(Traveling Salesman Problem)又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访 \(n\) 个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
最早的旅行商问题的数学规划是由 \(Dantzig(1959 )\) 等人提出,并且是在最优化领域中进行了深入研究。许多优化方法都用它作为一个测试基准。尽管问题在计算上很困难,但已经有了大量的启发式算法和精确方法来求解数量上万的实例,并且能将误差控制在 \(1\%\) 内。
对于旅行商问题,有一些较为广泛的解决方案(并非最优)。通常使用动态规划法、贪心法、分支限界法等等(包含但不仅限于回溯法、模拟退火算法、遗传算法、蚁群算法等等)进行对TSP问题的解决。这里提供的就是动态规划解法。
注:TSP问题的动态规划解法的空间复杂度较高,不适合城市数比较多的情况。
状压DP求解TSP问题例题
POJ 3311 Hie with the Pie
题目大意:
有N个城市(1~N且N<=10)要去送匹萨。一个PIZZA店(编号为0),求一条回路,从0出发,又回到0,而且距离最短(可重复走)。
分析:
首先我们要求这条路最短,那么这道题当中一定涉及到最短路,由于数据范围不大,又是多源,所以采用Floyd处理最短路。
下面考虑DP过程:
- 状态:\(dp[s][i]\) 表示当前对于所有城市的 \(0/1\) 状态为 \(s\) 的情况下,最后一个送到 \(i\) 号城市的最短距离。
- 转移:显然找到在当前状态中除了 \(i\) 的其他的所有点转移到 \(i\) ,并找到路径最小值。
- 答案:答案就是所有状态全为 \(1\) 的答案中的最小值,但是这里要求需要回到原点,需要加上当前点到原点的距离。
AC代码:
// #include
#include
#include
#include
using namespace std;
const int N = 12;
const int inf = 0x3f3f3f3f;
int n, dis[N][N], dp[1 << N][N];
void floyd() {
// 由于n很小,这里直接Floyd处理最短路
for (int k = 0; k <= n; k ++ ) {
for (int i = 0; i <= n; i ++ ) {
for (int j = 0; j <= n; j ++ ) {
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}
}
int main() {
while (1) {
scanf("%d", &n);
if (n == 0) {
break ;
}
for (int i = 0; i <= n; i ++ ){
for (int j = 0; j <= n; j ++ ) {
scanf("%d", &dis[i][j]);
}
}
floyd();
for (int s = 0; s <= (1 << n) - 1; s ++ ) {
for (int i = 1; i <= n; i ++ ) {
if (s & (1 << (i - 1))) {
if (s == (1 << (i - 1))) {
dp[s][i] = dis[0][i];
}
else {
dp[s][i] = inf;
for (int j = 1; j <= n; j ++ ) {
if (s & (1 << (j - 1)) && j != i) {
dp[s][i] = min(dp[s][i], dp[s ^ (1 << (i - 1))][j] + dis[j][i]);
// 经典状压转移操作,判断是否可以从j转移到i,如果可以则转移
// 注意,由于这个矩阵不是对称的,所以dis[i][j]和dis[j][i]并不一定相同
}
}
}
}
}
}
int ans = inf;
for (int i = 1; i <= n; i ++ ) {
ans = min(ans, dp[(1 << n) - 1][i] + dis[i][0]);
// 循环统计最小值,这里需要特殊注意由于最后要回到披萨店,所以要加上dis[i][0];
}
printf("%d\n", ans);
}
return 0;
} 五、状压DP的衍生
对于状压DP的衍生,通常指的就是:
基于连通性状态压缩的动态规划问题(插头DP、轮廓线DP)
而对于这个方面请参考原版论文:链接
六、总结
首先对于状压DP要理解的就是状态压缩。什么是状态压缩、怎么状态压缩、压缩之后有什么用,这个不仅仅是状压DP的基础,也是其他一类需要状态压缩来进行优化题的基础。
状态压缩适用于数据范围小(特指所压缩数据),并且类型相似(例如网格图)、决策简单(例如 \(0/1\) 选择)的DP情况。
在掌握状态压缩之前,掌握位运算可能是必须要做的事情。毕竟如果不会位运算的话,如何转移、如何压缩状态都是大问题。
在状压DP下,无论怎样做都没有改变动态规划无后效性、最优子结构的本质。所以状态压缩可以说是对于动态规划的一种优化方式或者是实现方式(由于真正实践上并没有在时间和空间上体现出有优化,理论上也没有进行优化,所以更偏向后者)。动态规划还是动态规划,状态、初值、转移方程和答案都要按照DP的方式一步一步设定好。
由于状压DP通常是对于每行进行压缩,而逐行处理。所以很多时候在赋初值的时候可能会涉及到对于一整排的赋值,当然也可能出现需要对前多排进行赋值。而答案也一样,不一定是某一个点的答案。由于我们只知道最后的状态,而不知道如何达到这个状态,所以在记录答案的时候,经常需要循环找到我们所需要的值(最大值、最小值、方案数)等等。
状态压缩这种方式也是其他很多题的优化方案之一。不妨将状态压缩也转化为一种考虑问题的方式(与 \(bitset\) 类似)。同样也可以吧状压看作是二进制优化的一种形式,对于解题可能有一些帮助。
借鉴与参考的部分网站:(乱序)
https://baike.baidu.com
https://www.cnblogs.com/Tony-Double-Sky/p/9283254.html
https://blog.csdn.net/forever_dreams/article/details/81074971
https://blog.csdn.net/u013377068/article/details/81054112
https://www.cnblogs.com/Ronald-MOK1426/p/8456945.html
https://www.luogu.org/
https://lydsy.com/JudgeOnline/