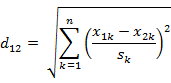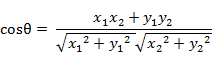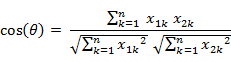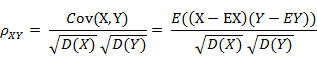阅读原文

相似性度量与距离

分类时常需要估算不同样本之间的 相似性度量 (Similarity Measurement)，这时通常采用的方法就是计算样本间的 “距离” (Distance)。采用什么方法计算距离很讲究，甚至关系到分类的正确与否。

1. 欧几里得距离 Euclidean Distance

两点形成的 直线的距离

欧氏距离

X = [0, 0; 1, 0; 0, 2]; % A,B,C 三点距离比较顺序 (A,B) (A,C) (B,C) 
D = pdist(X, 'euclidean'); % 1.0000    2.0000    2.2361

2. 曼哈顿距离 Manhattan/Cityblock Distance

两点所形成的线段 对轴产生的投影的距离总和。

城市街区距离。

坐标（x₁, y₁）的点 P₁ 与坐标（x₂, y₂）的点 P₂ 的曼哈顿距离为：

曼哈顿距离

X = [0, 0; 1, 0; 0, 2]; % A,B,C 三点距离比较顺序 (A,B) (A,C) (B,C) 
D = pdist(X, 'cityblock'); % 1     2     3

3. 切比雪夫距离 Chebyshev Distance

两点的 各坐标数值差的最大值。

maximum coordinate difference 最大的坐标轴差异。

(x₁,y₁) 和 (x₂,y₂) 的切比雪夫距离为 max(|x₂-x₁|,|y₂-y₁|)。

切比雪夫距离

X = [0, 0; 1, 0; 0, 2]; % A,B,C 三点距离比较顺序 (A,B) (A,C) (B,C) 
D = pdist(X, 'chebychev'); % 1     2     2

4. 闵可夫斯基距离 Minkowski Distance

闵氏距离不是一种距离，而是一组距离的定义。

欧式距离和曼哈顿距离的推广，p 是可变参数。

闵氏距离

其中 p 是可变参数。

当 p = 1 时，曼哈顿距离
当 p = 2 时，欧氏距离
当 p→∞ 时，切比雪夫距离

X = [0, 0; 1, 0; 0, 2]; % A,B,C 三点距离比较顺序 (A,B) (A,C) (B,C) 
D = pdist(X, 'minkowski');       % 默认p=2，为欧式距离
D1 = pdist(X, 'minkowski', 1);   % p=1，曼哈顿距离
D2 = pdist(X, 'minkowski', 2);   % p=2，欧式距离
D3 = pdist(X, 'minkowski', 3);   % p=3，闵3距离
D99 = pdist(X, 'minkowski', 99); % p=99，闵99距离
disp(D);                         % 1.0000    2.0000    2.2361
disp(D1);                        % 1         2         3
disp(D2);                        % 1.0000    2.0000    2.2361
disp(D3);                        % 1.0000    2.0000    2.0801
disp(D99);                       % 1         2         2  (接近切比雪夫)

5. 标准化欧氏距离 Standardized Euclidean distance

标准化欧氏距离先将 各个分量都 “标准化” 到均值、方差相等。
因为欧式距离中不同分量可能是不同的量纲，不能“相同看待”（闵式距离的缺点）

解决各分量的数据量纲差别大的问题，类比过拟合。

分量标准化，m 均值，s 标准差

标准化公式

两个 n 维向量：a(x₁₁, x₁₂, … , x_1n) 与 b(x₂₁, x₂₂, … , x_2n)

标准化欧氏距离

公式解释：
k = 1，x₁₁, x₂₁ 这组分量求出 m₁, s₁，然后用标准化公式得到 第1维 的标准化向量；
k = 2，x₁₂, x₂₂ 这组分量求出 m₂, s₂，然后用标准化公式得到 第2维 的标准化向量；
相当于，把各个分量的值都限制在 [-1, 1]。

标准化后，各分量的期望和方差都相同，m = 0，s = 1。

X = [0, 0; 1, 0; 0, 2]; % A,B,C 三点距离比较顺序 (A,B) (A,C) (B,C) 
D = pdist(X, 'seuclidean');                % 默认采用 实际标准差
D1 = pdist(X, 'seuclidean', [0.5, 1]);     % 自定义标准差
D2 = pdist(X, 'seuclidean', std(X, 0, 1)); % 使自定义标准差 = 实际标准差
disp(D)  % 1.7321    1.7321    2.4495
disp(D1) % 2.0000    2.0000    2.8284
disp(D2) % 1.7321    1.7321    2.4495

6. 马哈拉诺比斯距离 Mahalanobis Distance

马氏距离表示数据的 协方差距离，其考虑到各种特性之间的联系。

协方差，排除变量之间的相关性干扰。

设 M 个样本向量 X₁ ~ X_m，协方差矩阵记为 S，均值记为向量 μ。
则其中样本向量 X 到 μ 的马氏距离为：

X 到 μ 的马氏距离

其中向量 X_i 与 X_j 间的马氏距离为：

Xi 与 Xj 间的马氏距离

若协方差矩阵是单位矩阵（各个样本向量之间独立同分布）,则公式就成了：

S = 1

即为欧氏距离。

若协方差矩阵是 对角矩阵，公式变成了标准化欧氏距离。

X = [1 2; 1 3; 2 2; 3 1]; % A,B,C,D四点，(A,B)(A,C)(A,D)(B,C)(B,D)(C,D)
D = pdist(X,'mahalanobis'); % 2.3452    2.0000    2.3452    1.2247    2.4495    1.2247

7. 夹角余弦

几何中夹角余弦可用来衡量 两个向量方向的差异，
机器学习中借用这一概念来衡量样本向量之间的差异。

向量方向差异：[-1, 1]

① 二维空间中向量 A(x₁,y₁) 与向量 B(x₂,y₂) 的夹角余弦公式：

二维夹角

② n 维样本点 a(x₁₁,x₁₂,…,x_1n) 和 b(x₂₁,x₂₂,…,x_2n)：

n 维夹角

X = [1 0; 1 1.732; -1 0]; % A,B,C三点 (A,B)(A,C)(B,C)
D = pdist(X, 'cosine'); % matlab中该函数求得结果其实是 1 - cos(θ)
disp(D);   % 0.5000    2.0000    1.5000
disp(1-D); % 0.5000   -1.0000   -0.5000 得到cos(θ)

8. 汉明距离

① 两个等长字符串 s₁ 与 s₂ 之间的 汉明距离 定义为 将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。

一个字符串 s₁ 变化为另一个字符串 s₂ 需要的最小替换次数。

应用：信息编码（为了增强容错性，应使得编码间的最小汉明距离尽可能大）

② Matlab Hamming distance, percentage of coordinates that differ

X = [1 0; 1 1.732; -1 0]; % A,B,C三点 (A,B)(A,C)(B,C)
D = pdist(X, 'hamming'); % 0.5000    0.5000    1.0000

9. 杰卡德距离/杰卡德相似系数 Jaccard similarity coefficient

① 杰卡德相似系数：两个集合 A 和 B 的交集元素在 A，B 的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号 J(A,B) 表示。

杰卡德相似系数

杰卡德相似系数是 衡量两个集合相似度 的一种指标。

杰卡德相似系数：集合 ∩ / ∪

② 杰卡德距离与杰卡德相似系数相反：

杰卡德距离

杰卡德相似系数：1 - 集合 ∩ / ∪

用两个集合中不同元素占所有元素的比例 来 衡量两个集合的区分度。

③ Matlab Jaccard Distance, percentage of nonzero coordinates that differ

非零的坐标轴数值不同所占的比例。

X = [1 1 0; 1 -1 0; -1 1 0]; % (A,B)1/2 (A,C)1/2 (B,C)2/2
D = pdist(X, 'jaccard'); % 0.5000    0.5000    1.0000

X = [1 1 1; 1 2 1; 1 2 2]; % (A,B)1/3 (A,C)2/3 (B,C)1/3
D = pdist(X, 'jaccard'); % 0.3333    0.6667    0.3333

10. 相关系数/相关距离 Correlation Coefficient / Distance

① 相关系数的定义：

10种距离和相似性度量