【算法梗概】
点分治,是一种针对可带权树上简单路径统计问题的算法。本质上是一种带优化的暴力,带上一点容斥的感觉。
注意对于树上路径,并不要求这棵树有根,即我们只需要对无根树进行统计。接下来请把无根树这一关键点牢记于心。
【引入】
话不多说,先看一题:
给定一棵树,树上的边有权值,给定一个阈值\(k\),请统计这棵树上总长度小于等于\(k\)的路径个数。
路径长度为路径路径上所有边的权值和。
这就是POJ 1741。
题意描述很清楚,你是否已经有了想法?
考虑简单的DFS过程,能否统计答案?
DFS把树看作有根树,那么对于一个子树\(\mathfrak T\),根节点为\(t\),如何统计\(\mathfrak T\)中的路径个数(答案)?
我们考虑\(\mathfrak T\)中的路径。
把路径分为两种:
一、经过\(t\)的路径。
二、不经过\(t\)的路径。
这样分类是显然正确的,而且对于不经过\(t\)的路径,它们一定在\(t\)的某个子节点所构成的子树中。
这样就对答案进行了划分:树\(\mathfrak T\)的答案等于\(\mathfrak T\)中经过\(t\)的路径的答案加上\(t\)的所有子节点构成的子树的答案。
对于第二部分的答案,我们递归处理;现在考虑计算第一部分的答案,即计算经过\(t\)的路径的个数。
这里提供一种思路:
考虑路径的合并,利用容斥去除非法路径:
“路径的合并”说的是\(t\)到\(\mathfrak T\)中的任意一个节点(包括自身)的路径集合的合并。
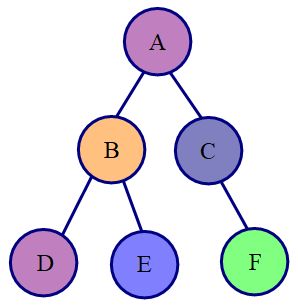
比如看下面这张图:
现在树根是\(A\)点,那么路径的集合是:\(\left\{\begin{matrix}A\\A\to B\\A\to B\to D\\A\to B\to E\\A\to C\\A\to C\to F\end{matrix}\right\}\)。
两两组合,共有\(C_{n+1}^{2}=C_{7}^{2}=21\)种不同的方式。但是显然有不合法的路径:比如\(A\to B\to D\;,\;A\to B\to E\)不能合并。
注意到一条路径可以简单地用路径的终点表示,那么共有子树节点个数条路径,而能够合并的路径只有在不同子树的路径,而在同一子树的路径无法合并。
当然,可以合并的路径也可能因为路径长度大于\(k\)而不能计入答案。
先不考虑非法的路径,看看如何统计长度小于等于\(k\)的路径:
- 通过一次DFS,把所有从根向子树的路径长度处理出来,在数组里排序,这一步时间为\(O(n\;log\;n)\),\(n\)为子树节点数。
- 通过双指针扫描的技巧,在\(O(n)\)的时间内计算答案;或者直接在数组内二分,在\(O(n\;log\;n)\)的时间内计算。
那么接下来考虑容斥去除非法的路径,对于根节点的每个子节点代表的子树,按照同样方式统计答案,并把得出的结果从原来的答案中减去即可。
真的就行了吗?
其实还要考虑子树的路径长度,刚才对根的计算时,子树的所有路径长都加上了根到子树的边的权值。
那么在对这棵子树计算时,注意子树的路径也都要加上这条边的权值,这样正好和原来的路径长度吻合。
或者,同样的道理,因为这条边多计算了两次,把\(k\)相应地减少\(2\)倍的这条边的权值也可以。
那么对于一个节点,总的时间复杂度为\(O(n\;log\;n)\),\(n\)为子树节点个数。
那么这样,就能对于一个节点的子树统计答案了,最终把所有答案加起来就行了。
但是,真的就行了吗?请看下一个内容。
【算法核心】
可以看到,计算一个节点的复杂度为\(O(n\;log\;n)\),但要保证总复杂度不超过一个量级却很难。
但是我们可以利用无根树的性质!
可以看到,把一个点的答案算完时,它的子节点所代表的子树就互不影响了!
就是说,这些子树彼此独立,可以完全当作一个新的子问题处理。
那么考虑如下算法:
- 对于这棵无根树,找到一个点,使得它在树的中心位置,满足如果以它为根,它的最大子树大小尽量小,这个点称为重心。
- 以这个点为根,计算它的答案。
- 把以这个点为根的树的所有子树单独作为一个子问题,回到步骤\(1\)递归处理。
这个算法的复杂度是多少呢?
先介绍一个定理:以树的重心为根的有根树,最大子树大小不超过\(\frac{n}{2}\)。
假设超过了,大小为\(k>\frac{n}{2}\),那么其他子树大小之和等于\(n-k-1\)。
那么把重心往这个子树方向移动,最大子树大小一定减小,因为\(n-k<\frac{n}{2} 那么进一步地,就证明了经过这个算法,递归的次数是\(O(log\;n)\)级别。 这样,就进一步说明了算法总时间复杂度不超过\(O(n\;log^2\;n)\)。 【算法实现】 按照上述步骤实现代码: ①计算重心位置:使用一次简单的DFS来实现。 ②计算答案:直接用另一个DFS计算。 ③分治子问题:重新调用寻找重心的DFS函数,再递归求解即可。 那么可以根据此,写出代码: 这是寻找重心的函数,需要传入父节点,还要调用vis数组。调用前保证Root等于0,并且wt[0]等于无限大。 注意第5行,Tsiz是当前处理的树的大小,这是因为把无根树转成有根树后,父亲所连的子树也是自己的孩子了。 这两个是计算答案的函数,Dfs统计路径长度,而calc计算答案,使用了双指针的技巧。 这是点分治的核心函数,传入的是当前树的重心,在调用时计算重心的答案。 然后求每个子树的重心,再递归求解。 对于刚刚的题目,有如下代码实现: 【总结】 点分治是经典的分治思想在树上的应用,是很重要的OI算法。 其精髓在于把无根树平均地分割成若干互不影响的子问题求解,极大降低了时间复杂度,是一种巧妙的暴力。 【注】 细心的读者可能已经发现,代码中在分治过程中,对下一层分治块的总结点数处理可能会出错,但是不影响复杂度,具体证明见http://liu-cheng-ao.blog.uoj.ac/blog/2969。void GetRoot(int u,int f){
siz[u]=1; wt[u]=0;
eF(i,u) if(to[i]!=f&&!vis[to[i]])
GetRoot(to[i],u), siz[u]+=siz[to[i]], wt[u]=max(wt[u],siz[to[i]]);
wt[u]=max(wt[u],Tsiz-siz[u]);
if(wt[Root]>wt[u]) Root=u;
}
void Dfs(int u,int D,int f){
arr[++cnt]=D;
eF(i,u) if(to[i]!=f&&!vis[to[i]]) Dfs(to[i],D+w[i],u);
}
int calc(int u,int D){
cnt=0; Dfs(u,D,0); int l=1,r=cnt,sum=0;
sort(arr+1,arr+cnt+1);
for(;;++l){
while(r&&arr[l]+arr[r]>k) --r;
if(rvoid DFS(int u){
Ans+=calc(u,0); vis[u]=1;
eF(i,u) if(!vis[to[i]]){
Ans-=calc(to[i],w[i]);
Root=0, Tsiz=siz[to[i]], GetRoot(to[i],0);
DFS(Root);
}
}
#include