Harmonious Army

Harmonious Army

Now, Bob is playing an interesting game in which he is a general of a harmonious army. There are n soldiers in this army. Each soldier should be in one of the two occupations, Mage or Warrior. There are m pairs of soldiers having combination ability. There are three kinds of combination ability. If the two soldiers in a pair are both Warriors, the army power would be increased by a. If the two soldiers in a pair are both Mages, the army power would be increased by c. Otherwise the army power would be increased by b, and b=a/4+c/3, guaranteed that 4|a and 3|c. Your task is to output the maximum power Bob can increase by arranging the soldiers' occupations.

Note that the symbol a|b means that a divides b, e.g. , 3|12 and 8|24.

Input

There are multiple test cases.

Each case starts with a line containing two positive integers n(n≤500) and m(m≤\(10^4\)).

In the following m lines, each line contains five positive integersu,v,a,b,c (1≤u,v≤n,u≠v,1≤a,c≤4×\(10^6\),b=a/4+c/3), denoting soldiers u and v have combination ability, guaranteed that the pair (u,v) would not appear more than once.

It is guaranteed that the sum of n in all test cases is no larger than 5×\(10^3\), and the sum of m in all test cases is no larger than 5×\(10^4\).

Output

For each test case, output one line containing the maximum power Bob can increase by arranging the soldiers' occupations.

Sample Input

3 2

1 2 8 3 3

2 3 4 3 6

Sample Output

12

思路：

把\(s\)连向\(u，v\)连容量为\(\frac{a+b}{2}\)的有向边\(,\)把\(u,v\)向\(t\)连容量为\(\frac{b+c}{2}\)的有向边\(，\)在\(u,v\)间连条\(\frac{a+c}{2}-b\)，用\(\sum_{i=1}^n(a_i+b_i+c_i)\)减最大流
如图：

证明：


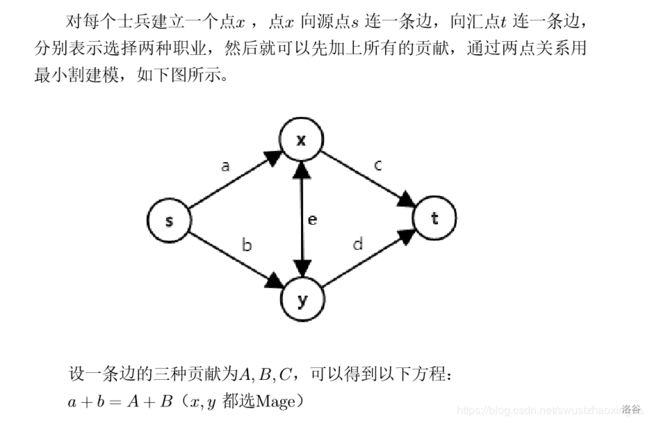
(这张图找了半天)


\[ \begin{cases} a+b=A+B&\\ c+d=B+C&\\ a+e+d=b+e+c=A+C \end{cases}\]

其中一组解为
\[ \begin{cases} a=b=\frac{A+B}{2}&\\ c=d=\frac{B+C}{2}&\\ e=\frac{A+C}{2}-B \end{cases}\]
便得到了上面建边的由来

\(\mathfrak{Talk\ is\ cheap,show\ you\ the\ code.}\)

#include
#include
#include
#include
#include
using namespace std;
# define read read1()
# define Type template
Type inline T read1(){
    T n=0;
    char k;
    bool fl=0;
    do (k=getchar())=='-'&&(fl=1);while('9'%d\n",u);
                for(int i=G.f[u];i;i=G.G[i].t){
                    if(!lev[G.G[i].u]&&G.G[i].v>0){
                        int to=G.G[i].u;
                        lev[to]=lev[u]+1;
                        q[t++]=to;
                        if(to==T)return 1;
                    }
                }
            }
            return 0;
        }
        double dfs(int u,double f){
            if(u==T)return f;
            double tag=0,c;
            for(int &i=cur[u];i;i=G.G[i].t){
                int to=G.G[i].u;
                if(G.G[i].v>0&&lev[to]==lev[u]+1){
                    c=dfs(to,min(f-tag,G.G[i].v));
                    G.G[i].v-=c;
                    G.G[(i-1^1)+1].v+=c;
                    tag+=c;
                    if(tag==f)return tag; 
                }
            }
            return tag;
        }
        double Dinic(){
            double ans=0;
            while(bfs()){
                for(int i=0;i++^n;)cur[i]=G.f[i];
                ans+=dfs(S,2e9);
            }
            return ans;
        }
    # undef Big
    # undef Big2
}G;
# define fre(k) freopen(k".in","r",stdin);freopen(k".out","w",stdout)
# define f(i,l,r) for(int i=l;i<=r;++i)
int main(){
    G.Into(1,2);
    int n,m;
    while(~scanf("%d %d",&n,&m)){
        double t=0;
        G.Clear();
        for(int i=0;i++^m;){
            int u=read,v=read;
            double A=read,B=read,C=read;
            t+=A+B+C;
            G.add(1,u+2,(A+B)/2);
            G.add(1,v+2,(A+B)/2);
            G.add(u+2,2,(B+C)/2);
            G.add(v+2,2,(B+C)/2);
            G.add(u+2,v+2,(A+C)/2-B);
            G.add(v+2,u+2,(A+C)/2-B);
        }
        printf("%.0f\n",t-G.Dinic());
    }
    return 0;
}