例题3:
n个人围成一圈,每个人有一些初始金币,可以分给左右相邻的人一些金币,最终使得所有人金币数量相同。求被转手的金币最少是多少。
要点1:
如果1号转给2号x个金币,2号转给1号y个,其实相当于1号转给2号num=x-y个金币,num>0表示金币实际从1到2,num<0表示从2到1
要点2:
设1号给n号x1个金币,2号给1号x2个金币...
记初始时第i个人有Ai个金币,最后的平均值是M,则有:
对第一个人:A1-x1+x2=M
对第二个人:A2-x2+x3=M
...
对第n个人:An-xn+x1=M
我们尝试将x2~xn都用x1表示出来,则有:
x2=M-A1+x1(记为x1-C1)
x3=M-A2+x2=M-A2+M-A1+x1(记为x1-C2)
...
xn=x1-Cn-1
于是如果要求转手的金币最小,实际上是要求|x1|+|x2|+...+|xn|最小
也就是|x1|+|x1-C1|+|x1-C2|+...|x1-Cn-1|最小
这就转换成了一维坐标轴上到固定点距离之和最小的问题,结论是取这些点的中位点
例题6:
有一个n * n * n的立方体,其中的一些单位立方体被挖去,剩余的每个单位立方体被涂上单一的颜色(即6个面颜色相同)。给出前后左右顶底的6个视图,求最多可以剩余多少个单位立方体
要点:
枚举所有单位立方体,找出一定不存在的单位立方体后删除。
一定要删除的单位立方体:
1.能“看穿”的位置所对应的所有单位立方体
2.在两个视图下颜色不同的单位立方体
不断迭代这个过程,直到所有剩下的立方体都不一定要删除。
例题8:
有n个带颜色的立方体,每个面都有一种颜色。要求重新涂尽量少的面,使得所有立方体完全相同
要点1:
一个立方体一共有24中不同的姿态(先确定顶面,然后从剩余的4个面中确定正面,立方体就唯一确定了。一共6*4种)
要点2:
如何得到24中不同姿态的面编号排列
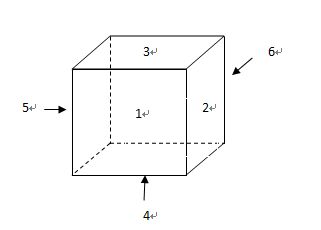
假设初始姿态如图所示
任意一个新的姿态都可以由初始姿态通过若干次“上旋”和“左旋”的组合得到
而旋转操作的本质是面的置换,以上旋为例
初始编号排列为{a1,a2,a3,a3,a5,a6}(分别代表0~5中的一个数)
上旋之后得到{a4,a2,a1,a6,a5,a3}
数组的对应关系为:
a[0]->b[2]
a[1]->b[1]
a[2]->b[5]
a[3]->b[0]
a[4]->b[4]
a[5]->b[3]
所以置换数组
int up={2,1,5,0,4,3};
同样可以得到
int left[]={4,0,2,3,5,1};
旋转函数:
void rot(int* T,int* p){
int q[6];
memcpy(q,p,sizeof(q));
for(int i=0;i<6;i++) p[i]=T[q[i]];
}
对int p[]={0,1,2,3,4,5}先做一次上旋再做两次左旋就可以表示为3次函数调用
rot(up,p);
rot(left,p);
rot(left,p);
要点3:
得到24中姿态后,取第一个立方体作为参照,枚举剩下的n-1个立方体的所有姿态,找到差异面数最小的那一种情况,复杂度为24^(n-1)
例题15:
给出一棵有n个节点的树,边长都为1,要求对其中一些节点打上标记,要求所有叶子节点到最近的标记节点的距离不超过K,求最少需要标记的节点数(初始时自带一个标记节点)
要点1:
以初始标记节点为根,将无根树转为有根树,并按节点深度分类,不同深度的节点放入node[dep]数组中
要点2:
按深度从小到大依次处理叶子节点,取当前最深的节点的K级父节点作为新的标记节点,并做一次DFS更新本次可以覆盖到的节点。
例题16:
n个人围成一圈,第i个人需要ai种不同的礼物。相邻的两个人所拥有的礼物不能相同。求最少需要多少种不同的礼物才能满足需求。
要点1:
n为偶数时比较简单,找到相邻两个人需要的数量和值最大的情况,记为M=a[k]+a[k+1],则对于奇数编号的人,取1 ~ a[i],对于偶数编号的人,取M-a[i]+1~M
要点2:
n为奇数是,用贪心+二分枚举测试。
贪心策略是:假设第一个人取了1 ~ a[1]的礼物,则后面的人,对于偶数编号的人,尽量从前面取;奇数编号的人,尽量从后面取。这样第n个人是奇数编号,所以会尽量从后面取,尽可能与第一个人的1 ~ a[i]避开。
最后判断编号为1与编号为n的人是否冲突来测试
例题19:
Floyd判圈算法:判断一个迭代计算的序列是否会出现环。
要点:
使用两个方法,第二个方法的迭代速度是第一个的两倍,若经过若干次计算,第一个的结果与第二的结果相等,则判断出现环。空间复杂度可以降到O(1)
例题22:
给出一个m * n的矩阵,有些格子是空地,有些格子是障碍。求出一个全是空地的最大子矩阵。
要点1:
从上到下枚举每一行作为矩形底边的情况下的最大子矩阵
要点2:
底边确定时,相当于是有一个序列a[],求Max{(j-i+1)a[k]|其中a[i]~a[j]都>=a[k]}
这个问题可以O(n)复杂度求解:
记left[i]为a[i]向左的满足a[k]>=a[i]的最长距离,这个left[]可以从左向右扫描,若a[i]<=a[i-1]则left[i]=left[i-1]+1,否则left[i]=1
同样的方法可以求right[]数组
那么ans=Max{(left[i]+right[i]-1)a[i]}