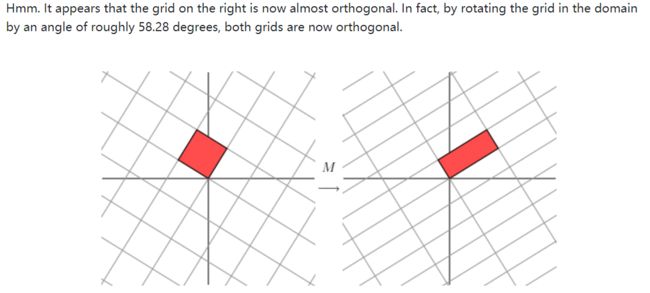
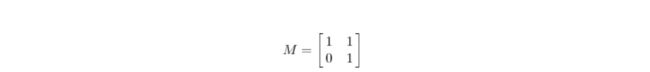复习一下SVD,这部分其实我之前一直理解得不太好,虽然知道SVD的一些实际应用,但理论部分一直有欠缺,这里补充学习一下。
(图引自http://www.ams.org/publicoutreach/feature-column/fcarc-svd)
文中提到,奇异值分解为分解矩阵提供了一种方便的方法,矩阵中可能包含一些我们感兴趣的数据,通过奇异值分解我们可以将矩阵分解为更简单、更有意义的部分。
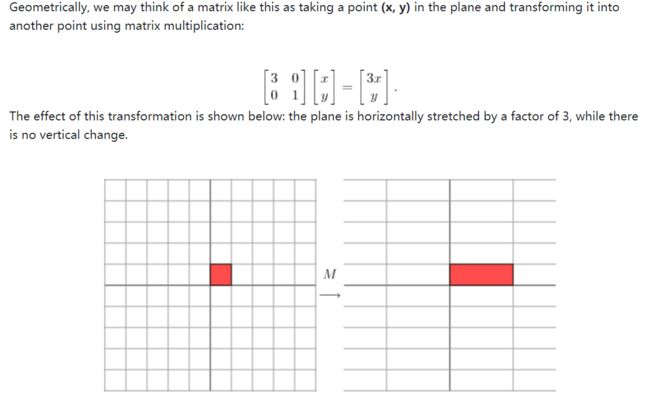
在探究奇异值分解前,我们先来看一下对角矩阵和对称矩阵的几何意义:
我们看到,对坐标点(x,y)左乘对角矩阵的几何意义就是“把平面水平拉伸3倍,垂直方向不变”,其实就是在坐标值不变的基础上,x轴的标度变为原来的3倍。再换一种更书面的表述就是,我们换了一组基,由{(1,0),(0,1)}换成了{(3,0),(0,1)}。
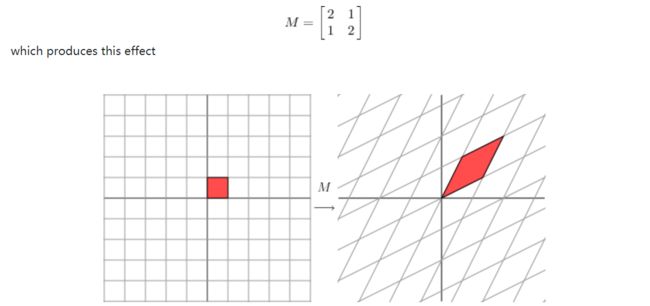
对称矩阵其实做的也是差不多的事,即换了一组基,由{(1,0),(0,1)}换成了{(2,1),(1,2)}。图中我们也能看到变换后的x轴上的unit vector就是(2,1)。
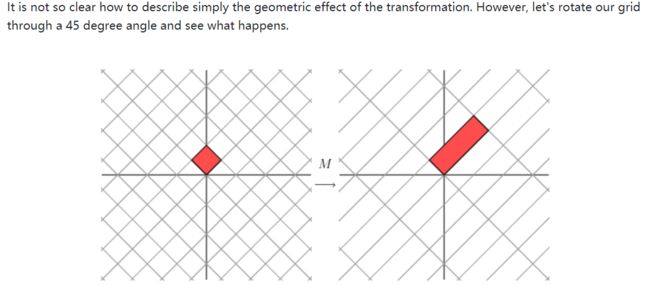
如果仅是这样描述矩阵乘法的作用,似乎并没有办法对矩阵分解和简化起到什么帮助,因为坐标系可以变成任何样子,基向量也可能不再垂直(比如这里的(2,1)和(1,2)),有没有一种方法使得我们变换后的坐标轴依然保持垂直呢?下面就是一例:
我们看到,左图的初始坐标系相比原坐标系逆时针旋转了45度,此时坐标(1,1)对应的向量如图所示,在此情形下我们的基向量实际上是()和(),因此左乘后得到的基向量为,即。不难发现,x轴方向的基向量扩大了三倍,y轴方向的基向量不变。这就又回到了对角矩阵变换的简单情形。
这其实就是所谓的特征向量和特征值的几何意义,即对某个基向量而言,左乘一个矩阵M相当于左乘一个标量,那么变换后的基向量就只发生伸缩不发生旋转。
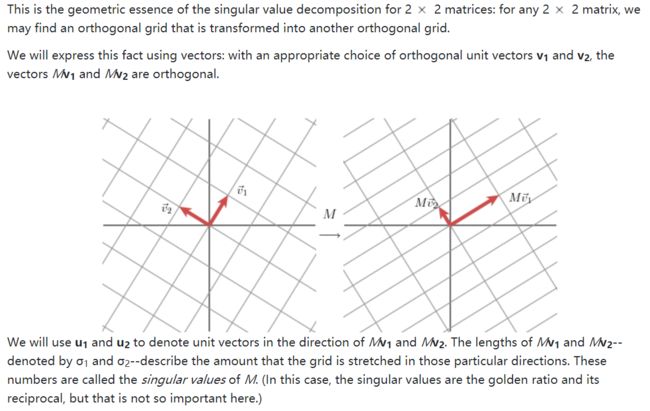
进一步,我们希望变换后的基向量两两正交,实际上对称矩阵的特征向量确实彼此正交(https://blog.csdn.net/DoctorCuiLab/article/details/82910837)这是很好的性质。之所以这么说是因为我们可以很容易的由初始坐标轴旋转至变换后的特征向量对应的坐标轴。
至此,我们已经可以知道对称矩阵运算具有的意义,一个对称矩阵所表示的线性变换相当于:
(1)把标准基上的坐标转化为以特征向量为基的坐标(坐标轴相互正交)
(2)在特征向量的方向上放缩特征值倍(伸缩变换)
(3)再把以特征向量为基的坐标转化为标准基上的坐标
实际上以上三步就对应着三个矩阵,这就是特征值分解,这是非常好的一种分解形式,原因暂且按下不表。我们现在想推广这种情形,首先,对于非对称矩阵如何呢?其实除了特征向量不正交以外,和上述步骤没什么差别。但是我们希望变换后的坐标系依然正交,因为这种各维度之间的独立性便于我们做分析和解释。
本例中我们看到,对于非对称矩阵M来说,可以找到一组正交基向量,其左乘M后会得到另一组正交向量。
一般的,对于矩阵M,我们希望找到一组正交基向量和,使其左乘矩阵M后得到的一组向量仍然彼此正交(对于对称矩阵来说,特征向量就是满足条件的和)。
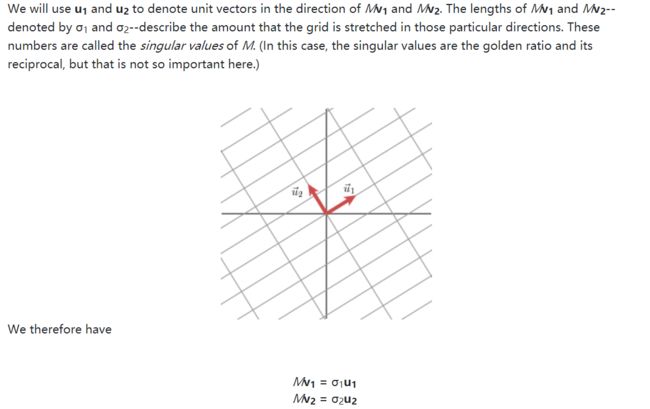
上图很好的表达了我们的意图,我们可以看到,标准正交基和左乘M后的向量依然正交,在此方向上(相比标准基)伸缩的倍数即为奇异值。
以上为奇异值分解的推导,我们看到,一个矩阵M可以被分解成三个矩阵,我们看一下x左乘M的时候()会发生什么事,首先我们的x对应的是标准基下的坐标,表示在和轴上的投影,即在和这组基上的坐标。接下来左乘对角矩阵,就得到了在和这组基上的坐标,最后左乘,得到在标准基下的坐标。整个过程清晰明了。
实际上,如果我们的,即变换前后的基相同,就得到了特征值分解,按上面的表述就是,我们先找到在特征向量方向上的坐标,然后伸缩特征值倍,最后再还原到标准基下的坐标。
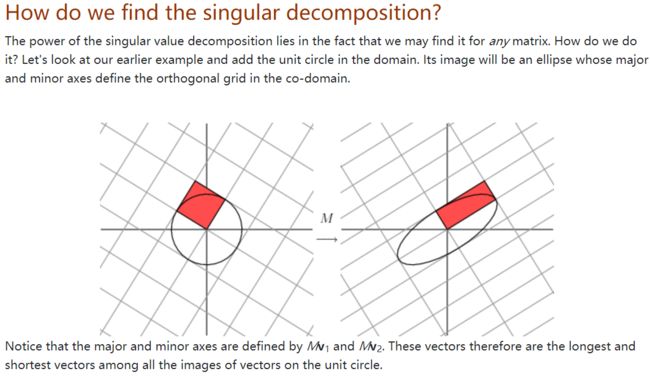
奇异值分解有哪些好处呢?直观的几何解释如下:
我们看到,原坐标系中的单位圆在变换后将变成新坐标系中的椭圆,而我们得到的基向量和对应的方向恰为椭圆的长轴和短轴方向。也就是变化最大和最小的方向,这在应用中具有很好的实际意义。
接下来我们看一下SVD分解如何得到。这里借助的是由上面的几何表示得出的直观结论,即我们希望找到的和分别对应使得的模最大和最小的。可以证明,这个解是的特征向量,这样我们就得到了。
找到了和,奇异值也就有了,即,以奇异值为对角元素得到。
最后我们可以求解确定。至此奇异值分解就完成了。