请尊重作者的劳动成果,如需转载请注明出处,谢谢!
如果觉得不错,可以关注我或者点赞,这就是你们对我最大的鼓励!
快速排序,作为应用最广泛的排序算法,实现简单,不仅速度比其他算法快(一般情况下),而且所需要额外的空间非常小。之前我们学习过的算法都无法将这两个优点结合起来。
然而,在实现的时候我们要非常小心,否则,快速排序的性能会变得低劣。
快速排序是通过递归地将数组分别两边(注意不是两半),一边小于基准数,另一边大于基准数 来实现排序的。
将数组分成两边在这里称为 “切分” partition。
那么,基准数是什么呢?基准数就是参考数,用来将数组分成两边的数。
多说无益,我们看示意图
假设我们现在将上图排序。为了方便,我们取第一个数为参考数。
“切分”的结果是
可以看到,在基准数 "4"的左边,所有的数都比它小,在它右边的数字都比它大。
那么,如何实现切分呢?关键就是要找到基准数 "4" 的恰当位置,并且以 "4" 为界,左边的数都小于它,右边的数都大于它。
快速排序的切分是这样的
从数组的头和尾开始扫描,从头部开始扫描
直至发现比基准数大的数,在那个位置停下来
然后尾部开始往前扫描
发现比基准数小的数时,停下来,如果 i < j 就交换 array[i] 和 array[j]
交换后得到
重复上面过程,得到
此时, i >= j 因此,array[i] 与 array[j] 不交换,
我们可以发现, j 前面的数都比基准数小,i 后面的数都比基准数大。因此 基准数正确的位置我们就找到了。
将基准数与 array[j] 交换就得到切分后的数组
和归并排序一样,我们对左边进行同样的操作,然后对右边也进行同样的操作,就可以将数组排序好。
示意图如下
头部和尾部进行扫描
i >= j 因此 array[i] 与 array[j] 不交换。并且将 基准数与 array[j] 交换得到
对1,2进行切分
头部尾部进行扫描
i >= j 因此 array[i] 与 array[j] 不交换。并且将 基准数与 array[j] 交换,即自己与自己交换,此时得到
最终,排序的结果为
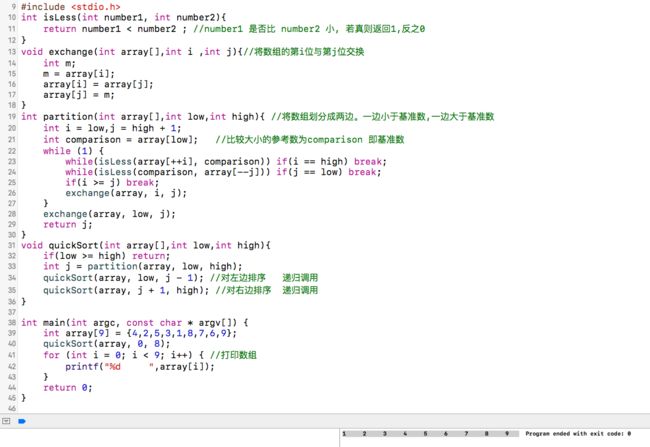
用C语言如下图
快速排序的内循环将数组元素与一个定值比较,这种简洁性是快速排序的一个优点。
快速排序的另一个速度优势在于它的比较次数很少。
快速排序的时间复杂度为NlogN级别。在最坏的情况下,比如第一次从最小的元素切分,第二次从第二小的元素切分,如此这般,每次调用只会移除一个元素。这样就会极其低效。为了避免这种情况,快速排序前我们将数组随机排序,将产生糟糕的切分的概率降到极低。
关于改进,我们说过,当数组几乎有序的情况或者数组较小时,插入排序的效率很高,所以可以作为判断,将 quickSort函数中 if(low >= high) return; 改成 if(high <= low + number) { insertionSort(array, low, high); return; } number的取值在 5 到 15 一般情况下都能令人满意。