Background:
首先声明一点,这篇博客不是我的原创,我被作者对大家习以为常的数据而具有深入细微的思考方式所折服,花了两天时间把数据下载下来,并且重现了原作者的过程和结论。原文链接[blog1] [blog2],我的这篇博客是综合以上两篇博客写成的。如有误会原作者的意思或者缺漏,请大家指正!
Part 1: 研究问题:
在美国西雅图市,好像人们对自行车越来越喜欢了,从越来越多的自行车俱乐部可以看出端倪。在我们的传统印象中,似乎骑自行车只是作为业余爱好,那么在西雅图是不是也是这种情况呢,自行车的使用情况随着周一到周末会有怎么样具体的变化呢,天气又对人们使用自行车的决定有多大的影响呢,下面我将尝试着回答这些问题。
Part 2:研究工具
本文使用的是python3.4+ipython notebook + pandas + numpy +sklearn,,其实以上的这些只用装一个Anaconda就可以完全解决了,数据是开源的,所有的结果是完全可重现的。
Part 3: 让数据说话
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
hourly = pd.read_csv(r"E:\研究生阶段课程作业\python\好玩的数据分析\SeattleBike-master\FremontHourly.csv",parse_dates=True,index_col="Date")#读入数据,同时默认“Date作为index”
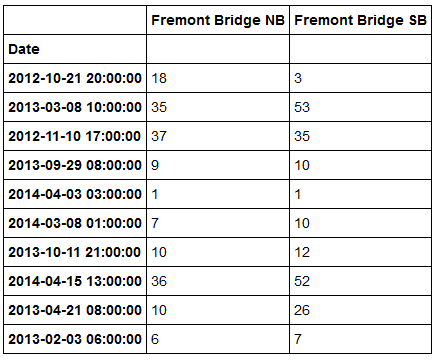
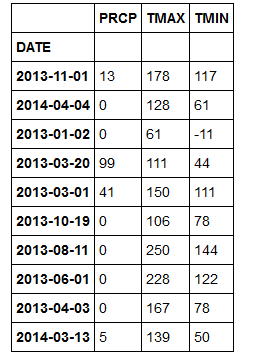
hourly.sample(n = 10) #随机抽取10行查看情况
上面的几行代码,首先是我们读入数据,这些数据可以在作者的 github直接下载,当然你也可以联系我,我会邮件给你。在这里我们读入数据的时候,做了一些小的处理,把csv文件中的"Date"字段当做日期处理。
hourly.columns = ['northbound', 'southbound'] #把列名改的简单一些,两个列名代表自行车经过时的方向。
hourly["total"] = hourly.northbound + hourly.southbound #新加一列,计算每个时刻自行车的总数
daily = hourly.resample("d",how='sum') #对数据框的日期按照天进行重采样,属于同一天的加在一起
weekly = daily.resample('w', how = 'sum') #对数据框的日期按照天进行重采样,属于同周的加在一起
weekly.plot()
从可视化结果上看,我们的第一眼直觉告诉我们,在2014年5月左右,西雅图街上的自行车最多,超过了32000/每周,上图,我们可以隐约看出来和2013年相比,2014年的自行车数量有所增加.
另外我们发现,夏天好像人们使用自行车的数量会异常的多,难道是夏天人们更愿意骑自行车吗,还是因为夏天,白昼时间会更长一些导致的呢。
def hours_of_daylight(date, axis=23.44, latitude=47.61):
"""Compute the hours of daylight for the given date
date: exmple:2012-10-07
axis: 地区的经度
latitude: 地区的纬度
return :how many hours a day
"""
diff = date - pd.datetime(2000, 12, 21)
day = diff.total_seconds() / 24. / 3600
day %= 365.25
m = 1. - np.tan(np.radians(latitude)) * np.tan(np.radians(axis) * np.cos(day * np.pi / 182.625))
m = max(0, min(m, 2))
return 24. * np.degrees(np.arccos(1 - m)) / 180.
“hours_of_daylight”只是用来计算某一天的白天有多少个小时的,这和天文学相关了,不用管具体原理了。
daily["day_of_hours"] = daily.index.map(hours_of_daylight)
weekly["day_of_hours"] = weekly.index.map(hours_of_daylight)
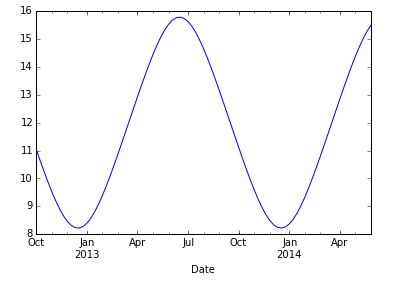
weekly.day_of_hours.plot() #绘出白天时长随着时间的变化图
果然美帝也是夏天有16个小时白天,冬天只有将近8个小时的白天啊。我们再研究一下2013-2014年,西雅图市每周自行车的数量变化和白天的长度是什么关系。
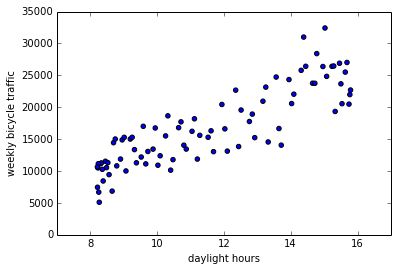
plt.scatter(weekly.day_of_hours,weekly.total)
plt.xlabel('daylight hours')
plt.ylabel('weekly bicycle traffic');
我们可以很明显的看出,随着白天的时间增加,活跃的自行车数量也在增加,而且感觉上还存在线性关系,所以先前我们说夏天人们骑自行车更多,可能只是因为夏天的白天时间长,并不是因为天气炎热之类的,当然这需要进一步的研究。
既然,白昼时间的自行车总数可能存在线性关系,那么我们来验证一下。
得益于scikit-learn,我们日常需要的机器学习方法在里面全部可以找到。我强烈建议翻看它的文档,我也在按步骤把scikit-learn翻译成中文。
from sklearn.linear_model import LinearRegression
X = weekly[['day_of_hours']] #白昼时间作为自变量
y = weekly['total'] #自行车数量作为应变量
clf = LinearRegression(fit_intercept=True).fit(X, y) #对上面两个变量进行线性拟合
print(clf.coef_)
out: 2056.44964989 #按照这个线性模型,白昼时间每增加一个小时,那么一周内观察到的自行车数量增加2056辆
print(clf.score(X,y))
out:0.74184335208140473 #计算线性模型对数据的拟合情况,结果越接近1,说明线性模型越精确
#为了更加直观看出我们建立的线性模型的预测效果,我们对预测结果和真实结果进行可视化对比
weekly["day_of_hours_trend"] = clf.predict(X) #利用模型去预测"total"
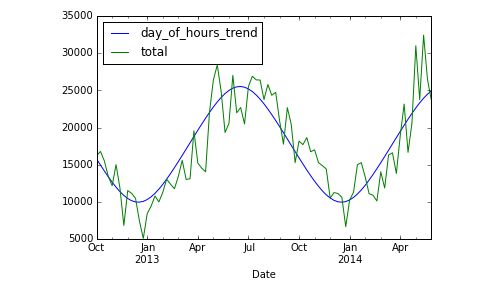
weekly[["day_of_hours_trend","total"]].plot() #利用模型预测值和真实值进行对比
我们可以认为我们建立的线性模型较为可靠,可以反应出街上的自行车数量随着白昼时间的变化。
回到我们当初的问题,一般在我们眼里,美帝人民使用自行车,那肯定用来休闲的,或者锻炼身体,那事情情况真是这样吗,我们继续挖掘。
days = ['Mon', 'Tues', 'Wed', 'Thurs', 'Fri', 'Sat', 'Sun']
def get_day_of_week(index):
return days[index.dayofweek]
daily["day_of_week"] = daily.index.map(get_day_of_week)
daily.head(10)
day_count = daily.groupby("day_of_week").total.sum().plot(kind = 'bar')
上面的代码就是新添一个列,对应每一个日期的星期几。,然后对星期1-7进行分租,按组求出自行车出行的总次数。结果如下:
这个结果出乎我们的想象,竟然周一到周五人们使用自行车的情况最多,周六和周末最少,看来美帝人民大部分是用自行车来上班的,并不是我们想象的只是骑着自行车来休闲的。到目前为止,影响西雅图人民选择自行车出行的方式已经有白昼的时长、星期几这两个因素了,下面我们再结合天气因素进行深一步的了解。
weather = pd.read_csv(r"E:\研究生阶段课程作业\python\好玩的数据分析\SeattleBike-master\SeaTacWeather.csv",index_col="DATE",parse_dates = True,usecols=[2,3,6,7]) #读入天气文件
关于西雅图市的天气情况,我们有现成的weather数据。
weather.sample(n = 10) #随机查看10行数据
#对温度和降雨量进行单位转化,转化到我们日常生活中的单位
weather['TMIN'] = 0.18 * weather['TMIN'] + 32
weather['TMAX'] = 0.18 * weather['TMAX'] + 32
weather['PRCP'] /= 254
weather.TMIN.plot() #绘出每日最高温随着时间的变化
weather.TMAX.plot() #绘出每日最低温随着时间的变化
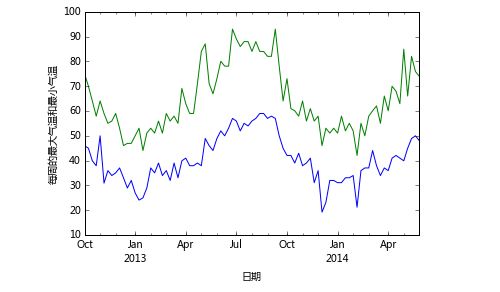
这种图简直就是密集恐惧症患者的灾难,为了更直观显示温度变化,我们对每周重采样,绘出每周的最低温和最高温随着时间的变化。
#按照每周进行时间规划,选出每周温度最大的和温度最小的,可视化
weather.TMIN.resample('w',how='min').plot()
weather.TMAX.resample('w',how='max').plot()
plt.xlabel("日期")
plt.ylabel("每周的最大气温和最小气温")
和上面的图相比,我觉得整个世界都清爽了呢。
我们现在拥有了天气、白昼时长、星期几这三个变量,下面的工作就是围绕这三个变量去预测自行车的数目变化,首先我们把天气信息放在一旁,只考虑每天的白昼时长和星期几,以这两个因素为自变量去预测街上自行车数量的变化.
daily_1 = daily
for i in range(7):
daily_1[days[i]] = (daily_1.index.dayofweek == i).astype(float)
daily_1.head(10)
这几行代码比较精简,也不容易理解,我来解释一下,首先是使用daily_1去备份daily这个数据框,然后为数据框增加7个列,分别是['Mon', 'Tues', 'Wed', 'Thurs', 'Fri', 'Sat', 'Sun'],为什么要这么做呢,因为在我们的线性预测模型中,我们使用的自变量必须是数值,但是我们的周几却是字符串变量,因此我们使用了一个小技巧对其进行了量化。我们可以直接看一下量化的结果:
我们观察变化后的结果,可以发现:“day_of_week”转化成了7列,而这7列的值都是数值,因此我们利用 “day_of_hours”和 ['Mon', 'Tues', 'Wed', 'Thurs', 'Fri', 'Sat', 'Sun']总共八个变量去预测自行车总数的变化。
X = daily_1[days + ['day_of_hours']]
y = daily_1['total']
clf = LinearRegression().fit(X, y)
daily_1['dayofweek_trend'] = clf.predict(X)
print(clf.score(X,y)) #检验线性拟合的效果
out: 0.68
(np.abs(daily_1.total - daily_1.dayofweek_trend)).mean() #计算模型预测值和真实值之间的平均误差
out: 532.11
从计算的结果可以看出,我们利用两个给出的信息,分别是星期几和白昼时长,我们就可以判断,这个某一天西雅图市街上的自行车总数,平均误差在532辆。
因为我们手里也有西雅图市的天气资料,我们决定加上天气这个选项,联合上面的两个因素,继续做预测。理想的情况是,我们手里的信息越多,预测的结果会越来越准确,那么结果真的是这样吗,我们继续向下探索。
如果你是沿着这篇博客从开始看到这里,你就应该知道,我们现在有两个数据框:
daily和weather,现在我们需要合并这两个数据框,使用降水量、温度、白昼时长、和星期几去预测街上自行车的数目。
daily_new = daily_1.join(weather,how = 'inner')##对daily 和 weather按照index,进行合并
#使用合并后的数据进行计算:包括周几,每天白昼有几个小时,温度的最大和最小值,降雨量作为自变量去预测每天的自行车总数
columns = days + ['day_of_hours', 'TMIN', 'TMAX', 'PRCP']
X = daily_new[columns]
y = daily_new['total']
clf = LinearRegression().fit(X, y)
daily_new['overall_trend'] = clf.predict(X)
(np.abs(daily_new.total - daily_new.overall_trend)).mean()
out: 365
这次我们使用了五个变量去预测某一天街上自行车的数量,和前面只用两个因素得到的532辆平均误差相比,现在的平均误差只有365,我们的预测结果越来越好了哇。
我们来看降雨量这个因素的影响,首先我们需要控制其他变量不变的情况
ind = columns.index('PRCP')
slope = clf.coef_[ind]
print(slope)
out: -824.64
表明在保持其他变量不变的情况下,当降雨量增加一英尺,街上的自行车数量差不多减少824辆.
Part 4: 结论
为了尊重原作者,我也把全部内容分成两部分来完成,分别是初步和进阶,在这篇博客中,主要用到了pandas的数据清洗和分析工作,同时也用到了sklearn中回归预测的知识,非常的简单,但是产生了较好的预测效果。所有的数据都是可以下载的,重复这些代码也是能够完全重现以上的这些结果的,如果你有疑问,那么可以参考英文原博客[blog1] [blog2],和原作者的github可以下载完整的代码和数据,如果我翻译有不到位的地方,希望你能够联系我,进行指正。
Life is short, I use python
Emial: [email protected]
QQ: 1527927373