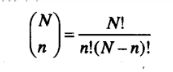学习了商务统计概率的几章,自认为已经理解了概率这块的知识,到最后发现自己能做的仅仅是罗列书上的概念和证明前人已经证明过的公式,这点让人十分沮丧。原来看懂了学会了是一回事,能够给别人讲明白又是另一回事。
本文是对概率学习的总结,涵盖了概率论中主要的基础知识:具有代表性的离散型随机变量——伯努利实验和二项分布及泊松分布的相关知识,连续型随机变量包含了正态分布和指数分布这些在现实生活中常见到的概率分布类型。
概率:用数值来描述事件发生的可能性,等于要测定的事件数目与全部可能发生的偶然事件总数之间的比率。
概率分布用来描述这一系列数值的规律。
概率论中对实验的定义是:能够产生明确结果的过程,投硬币、抛骰子、明天下不下雨、公交车上有几个人,这些都是实验。而所谓随机变量,是对实验结果的数值性描述。例:
- 定义实验(X)为投硬币,正面记为1,反面记为0,则X=0 或X=1
- 定义实验(X)为明天的降雨量,则X大于等于0,小于250毫米(一般来说)
通常用大写英文字母表示随机变量,这是约定。
随机变量根据其取值特征,分为离散型和连续型。
离散型随机变量
实验结果是由可逐一列举的结果组成的,那这个结果就是离散型随机变量。满足
- 每一种结果的可能性都是小于等于1的
- 所有结果的概率之和为1
比如上面列举的投骰子事件,一个均匀的骰子,结果必然是在1,2,3,4,5,6之中的一个,而且每个的概率相等,投一次骰子必然出现上述结果中的一个。那么每个结果的概率就是1/6。
离散型随机变量的方差:
其中x i为每一个事件,P i表示当前事件发生的概率。
连续随机变量中有一种特殊事件,只会产生两种结果,并且重复这一实验每次的结果不会影响其他实验(独立实验),称为伯努利实验。
伯努利实验
期望E(x) = p
方差D(x) = p(1-p)
二项分布
进行一次伯努利实验叫做1重伯努利实验,进行两次伯努利实验叫做2重伯努利实验,以此类推。统计学中管N次伯努利实验的结果分布称为二项分布。
以投硬币来说,(投硬币是很标准的伯努利实验,结果只有正反两面,每次投硬币不影响其他次)重复10次,即10重伯努利实验,查看正面朝上的次数,把10重伯努利实验看做一个试验,随机变量X的取值是正面朝上的次数,则X=0,1,2,3,4,5,6,7,8,9,10 每种结果的概率不尽相等。
其分布服从:
二项概率的期望:
p为每一次实验中正面的概率。
方差:
泊松分布
泊松分布的作用是描述一段时间内(或者一段空间中)某一事件发生的次数:比如医院每天接收到的病人数,呼叫台收到的求助电话,或者一段高速公路上道路的损坏量。
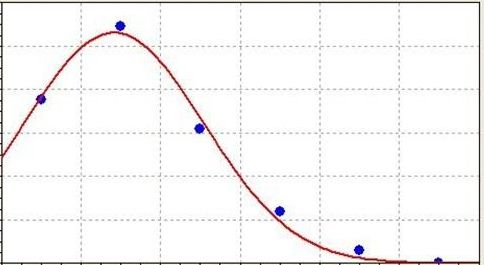
比如说,医院每天接诊的病人数量是不固定的,单是理论上讲,最少是0人,最多可以无限多,但是总有一个平均值,不妨设为100人。那么医院接诊人数的概率分布大概是这样的:
最左侧为零概率很小,最大可能100人在峰顶,随着人数增多,概率降低。其概率分布服从:
μ表示均值。
连续型随机变量
如果实验结果取值是无限的,比如明天降雨量可能是10~50mm之间任意小数,可以用离散随机变量来表示这一事件。
正态分布
正态分布是一种特殊的分布类型,自然界中非常常见:同龄人中体重分布、商品价格、家电使用寿命等。
正态分布的图形和函数:
正态分布具有如下特性:
- 正太分布有一个完整的家族,通过μ和σ来区分
- 均值=中位数=众数
- 均值可以是任意数值
- 正态分布是关于均值对称的,且两端无限延伸永远不会和X轴相交
- 标准差越大,曲线越平滑
- 曲线下的总面积是1
- 经验法则:
在正态分布中,几乎所有数据都将落在均值的三倍标准差内:
一个标准差内的数据包含68.26%
两个标准差内含有95.44%的数据
三个标准差内含有99.75%的数据
为了便于计算,统计学家又创造了一个特殊的工具——标准正态分布。
标准正态分布
规定均值μ=0,标准差σ=1的正态分布为标准正态分布,因为在标准正态分布中,根据标准正态分布表可以方便查找某一数值内的概率值。将非标准正态分布转换为标准正态分布的公式是:
得到的Z其实就是,当前X距离均值μ有多少个标准差,然后在标准正态分布表中查找概率即可。
指数概率分布
之前讲到的泊松分布,用于描述单位时间内某一独立事件发生的次数,如果说1小时之内有10个人被送往医院,那么我们有没有理由得出一个结论:在进入医院的这些人中,平均每两个人间隔的时间是6分钟呢?
指数概率分布就是用来描述这样的现实情况的,两个独立事件发生的间隔时间是遵循一定规律的。
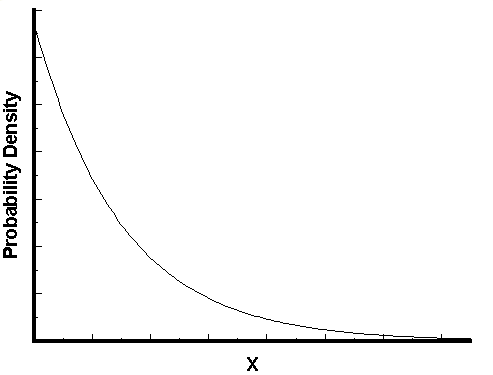
下一个病人进入医院的时间遵循下图:
用公式表示:
那么指数概率函数的概率值怎么计算呢?
我们知道,对于连续型随机变量,函数曲线下方的面积表示某一范围内实验成功的概率。
如果医院平均每小时接诊10个病人,等价于平均每隔6分钟就有一个病人入院,如何计算接下来10分钟都没有病人来的概率?
对f(x)进行积分,得到指数概率函数的积分函数
十分钟内有病人来的概率P=f(10)-f(x),μ=6,x=10
带入公式,解得p=0.81,也就是说医院10分钟内有病人的概率为81%,那么没有病人来的概率就是1-p=18.9%
R练习
R是为统计而生的语言,而概率又是统计的左右手,那么R中必然涵盖了最丰富最实用的概率函数。
生成一个取值为(1,2,3,4,5)的离散型随机变量
S <- 1:5
sample(S,1)
sample函数是取样函数,语句表示在总体S中取样本容量为1 的样本。
连续型随机变量:
runif(10,0,1)
生成一个连续随机变量的结果集,最大值为1,最小值为0,总共产生10个结果。
求总体的描述统计量:
variable <- runif(20,0,10)
> variable
[1] 9.9773127 0.9068249 2.9146913 5.2424507 6.3117907 1.5062919 9.3339532
[8] 8.5417427 1.7908430 8.0426071 1.1718775 7.0559799 4.2752455 3.9599596
[15] 0.8790662 6.6649594 6.6439971 3.5650826 9.6578847 5.1773152
#均值
mean(variable)
[1] 5.180994
#方差
var(variable)
[1] 9.306402
#标准差
sd(variable)
[1] 3.05064
众数
S<-c(1,2,3,3,3,7,7,7,7,9,10,21)
which.max(table(S))
二项分布
在排列组合中有一计数法则,公式为
计算相当繁琐,在R中不必这么大费周章,因为R中有choose函数,用来计算从N中取n个的结果。
choose(10,5)就表示从10个中取5个共有多少总可能。
以投硬币为例,设共计投10次,每次正面概率1/2,每种结果的概率为choose(10,x)*(1/2)^10,且所以结果概率和为1。
(1/2)^10
x <- 0
for(i in 0:10){
x <- x + choose(10,i)*(1/2)^10
}
x=1
binom是R中的二项分布函数族,包含密度函数(dbinom),累积分布函数(pbinom),分为函数(qbinom),以及随机数函数(rbinom)
投10次硬币,结果为5次正面的概率
dbinom(5, 10, .5)
[1] 0.2460938
这跟手动计算的结果是一样的,可互相验证。
choose(10,5)*(1/2)^10
[1] 0.2460938
累计分布函数,正面大于5(包含6,7,8,9,10)的概率
pbinom(5,10,.5)
[1] 0.6230469
这是正面数0~5的累计概率,大于5的概率为
1-pbinom(5,10,.5)
[1] 0.3769531
手动验证:
l<- c(6,7,8,9,10)
p <- 0
for(i in l){
p <- p + choose(10,i)*(1/2)^10
}
p
[1] 0.3769531
正确!
rbinom可生成二项实验结果集
rbinom(100,10,.5)表示每轮进行10次实验,共进行100轮,每次实验的概率是1/2 ,返回结果成功次数的结果集。
[1] 6 5 6 7 6 6 5 4 8 6 7 6 3 4 5 5 6 4 4 8 6 3 3 3 3 5 3 7 3 6 4 6 6 5 3 3
[37] 4 6 6 3 5 6 2 5 4 6 5 3 6 6 5 3 5 8 6 3 6 4 5 4 2 3 5 3 6 5 6 5 8 5 6 6
[73] 2 4 4 5 8 5 3 6 4 7 8 4 6 7 5 5 2 6 7 3 2 3 8 5 2 5 3 5
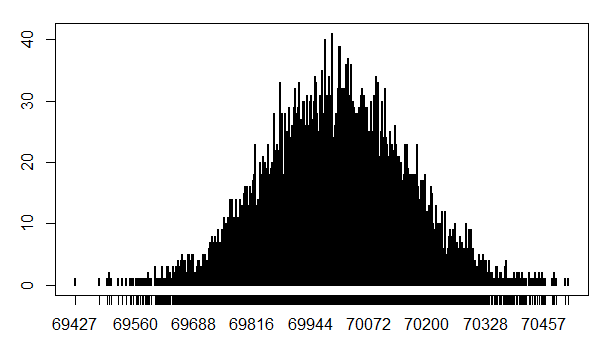
plot(table(res))
这是进行100次每次10个实验的结果,如果数值设置大一点,结果就很接近正态分布了。