树的定义与基本术语
树型结构是一类重要的非线性数据结构,其中以树和二叉树最为常用,是以分支关系定义的层次结构。树结构在客观世界中广泛存在,如人类社会的族谱和各种社会组织机构;在计算机领域中也有广泛应用,如在编译程序中,可用树来表示源程序的语法结构;在数据库系统中,树型结构也是信息的重要组织形式之一;在机器学习中,决策树,随机森林,GBDT等是常见的树模型。
树(Tree)是n(n≥0)n(n≥0)个结点的有限集。在任意一棵树中:(1)有且仅有一个特定的称为根(Root)的节点;(2)当n>1n>1时,其余节点可分为m(m>0)m(m>0)个互不相交的有限集T1,T2,...,Tm,T1,T2,...,Tm,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
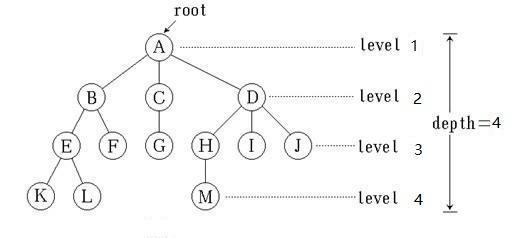
在图1,该树一共有13个节点,其中A是根,其余节点分成3个互不相交的子集:T1={B,E,F,K,L}T1={B,E,F,K,L},T2={C,G}T2={C,G},T3={D,H,I,J,M}T3={D,H,I,J,M};T1,T2和T3T1,T2和T3都是根A的子树,且本身也是一棵树。例如T1T1,其根为B,其余节点分为两个互不相交的子集;T11={E,K,L}T11={E,K,L},T12={F}T12={F}。T11T11和T12T12都是B的子树。而在T11T11中E是根,{K}{K}和{L}{L}是E的两棵互不相交的子树,其本身又是只有一个根节点的树。
接下来讲一下树的基本术语。
树的结点包含一个数据元素及若干指向其子树的分支。节点拥有的子树数量称为节点的度(Degree)。在图1中,A的度为3,B的度为2,C的度为1,F的度为0。度为0的结点称为叶子(Leaf)结点。在图1中,K,L,F,G,M,I,J都是该树的叶子。度不为0的结点称为分支结点。树的度是指树内个结点的度的最大值。
结点的子树的根称为该结点的孩子(Child),相应地,该结点称为孩子的双亲(Parent)。在图1,中,D是A的孩子,A是D的双亲。同一个双亲的孩子之间互称兄弟(Sibling)。在图1中,H,I,J互为兄弟。结点的祖先是从根到该结点所经分支上的所有结点。在图1中,M的祖先为A,D,H。对应地,以某结点为根的子树中的任一结点都称为该结点的子孙。在图1中,B的子孙为E,F,K,L。
树的层次(Level)是从根开始,根为第一层,根的孩子为第二层等。双亲在同一层的结点互为同兄弟,在图1中,K,L,M互为堂兄弟。树中结点的最大层次称为树的深度(Depth)或高度,在图1中,树的深度为4。
如果将树中结点的各子树看成从左到右是有次序的(即不能交换),则称该树为有序树,否则为无序树。
森林(Forest)是m(m≥0)m(m≥0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。在机器学习模型中,决策树为树型结构,而随机森林为森林,是由若干决策树组成的森林。
二叉树的定义与基本性质
二叉树(Binary Tree)是一种特殊的树型结构,它的特点是每个结点至多有两棵子树(即二叉树中不存在度大于2的结点),且二叉树的子树有左右之分,其次序不能任意颠倒(有序树)。
根据二叉树的定义,其具有下列重要性质:(这里不给出证明,证明细节可参考清华大学出版社 严蔚敏 吴伟民的《数据结构(C语言版)》)
性质1)在二叉树的第ii层上至多有2i−12i−1个结点(i≥1)(i≥1)。
性质2)深度为kk的二叉树至多有2k−12k−1个结点(k≥1)(k≥1)。
性质3)对任何一棵二叉树,如果其叶子节点数为n0n0,度为2的结点数为n2n2,则n0=n2+1n0=n2+1。
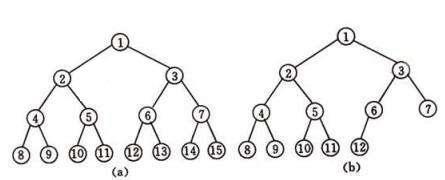
一棵深度为kk且有2k−12k−1个结点的二叉树称为满二叉树。深度为kk,结点数数nn的二叉树,当且仅当其每一个结点都与深度为kk的满二叉树中编号为1至n的结点一一对应时,称之为完全二叉树。在下图2中,(a)为满二叉树,(b)为完全二叉树。
下面介绍完全二叉树的两个特性:
性质4)具有nn个结点的完全二叉树的深度为[log2n]+1[log2n]+1,其中[x][x]表示不大于x的最大整数。
性质5)如果对一棵有n个结点的完全二叉树的结点按层序编号(从第一层到最后一层,每层从左到右),则对任一结点i(1≤i≤n)i(1≤i≤n),有:
(1)如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲结点为[1/2]。
(2)如果2i>n,则结点i无左孩子;否则其左孩子是结点2i。
(3)如果2i+1>n,则结点i无右孩子;否则其右孩子是结点2i+1。
介绍完了二叉树的定义及基本性质,接下来,我们需要了解二叉树的遍历。所谓二叉树的遍历,指的是如何按某种搜索路径巡防树中的每个结点,使得每个结点均被访问一次,而且仅被访问一次。对于二叉树,常见的遍历方法有:先序遍历,中序遍历,后序遍历,层序遍历。这些遍历方法一般使用递归算法实现。
先序遍历的操作定义为:若二叉树为空,为空操作;否则(1)访问根节点;(2)先序遍历左子树;(3)先序遍历右子树。
中序遍历的操作定义为:若二叉树为空,为空操作;否则(1)中序遍历左子树;(2)访问根结点;(3)中序遍历右子树。
后序遍历的操作定义为:若二叉树为空,为空操作;否则(1)后序遍历左子树;(2)后序遍历右子树;(3)访问根结点。
层序遍历的操作定义为:若二叉树为空,为空操作;否则从上到下、从左到右按层次进行访问。
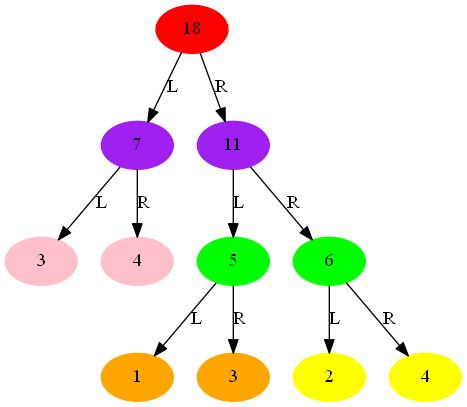
如对于下图3,
其先序遍历、中序遍历、后序遍历、层序遍历的结果为:
先序遍历为:
18 7 3 4 11 5 1 3 6 2 4
中序遍历为:
3 7 4 18 1 5 3 11 2 6 4
后序遍历为:
3 4 7 1 3 5 2 4 6 11 18
层序遍历为:
[[18], [7, 11], [3, 4, 5, 6], [1, 3, 2, 4]]
关于二叉树的存储结构,可以选择链式存储结构。用于表示二叉树的链表中的结点至少包含3个域:数据域和左、右指针。下面会给出如何利用利用链式存储结构实现二叉树(Python实现)。
二叉树的Python实现
了解了二叉树的基本情况后,笔者使用Python实现了二叉树,其完整的Python代码(Binary_Tree.py)如下:
from graphviz import Digraph
import uuid
from random import sample
# 二叉树类
class BTree(object):
# 初始化
def __init__(self, data=None, left=None, right=None):
self.data = data # 数据域
self.left = left # 左子树
self.right = right # 右子树
self.dot = Digraph(comment='Binary Tree')
# 前序遍历
def preorder(self):
if self.data is not None:
print(self.data, end=' ')
if self.left is not None:
self.left.preorder()
if self.right is not None:
self.right.preorder()
# 中序遍历
def inorder(self):
if self.left is not None:
self.left.inorder()
if self.data is not None:
print(self.data, end=' ')
if self.right is not None:
self.right.inorder()
# 后序遍历
def postorder(self):
if self.left is not None:
self.left.postorder()
if self.right is not None:
self.right.postorder()
if self.data is not None:
print(self.data, end=' ')
# 层序遍历
def levelorder(self):
# 返回某个节点的左孩子
def LChild_Of_Node(node):
return node.left if node.left is not None else None
# 返回某个节点的右孩子
def RChild_Of_Node(node):
return node.right if node.right is not None else None
# 层序遍历列表
level_order = []
# 是否添加根节点中的数据
if self.data is not None:
level_order.append([self])
# 二叉树的高度
height = self.height()
if height >= 1:
# 对第二层及其以后的层数进行操作, 在level_order中添加节点而不是数据
for _ in range(2, height + 1):
level = [] # 该层的节点
for node in level_order[-1]:
# 如果左孩子非空,则添加左孩子
if LChild_Of_Node(node):
level.append(LChild_Of_Node(node))
# 如果右孩子非空,则添加右孩子
if RChild_Of_Node(node):
level.append(RChild_Of_Node(node))
# 如果该层非空,则添加该层
if level:
level_order.append(level)
# 取出每层中的数据
for i in range(0, height): # 层数
for index in range(len(level_order[i])):
level_order[i][index] = level_order[i][index].data
return level_order
# 二叉树的高度
def height(self):
# 空的树高度为0, 只有root节点的树高度为1
if self.data is None:
return 0
elif self.left is None and self.right is None:
return 1
elif self.left is None and self.right is not None:
return 1 + self.right.height()
elif self.left is not None and self.right is None:
return 1 + self.left.height()
else:
return 1 + max(self.left.height(), self.right.height())
# 二叉树的叶子节点
def leaves(self):
if self.data is None:
return None
elif self.left is None and self.right is None:
print(self.data, end=' ')
elif self.left is None and self.right is not None:
self.right.leaves()
elif self.right is None and self.left is not None:
self.left.leaves()
else:
self.left.leaves()
self.right.leaves()
# 利用Graphviz实现二叉树的可视化
def print_tree(self, save_path='./Binary_Tree.gv', label=False):
# colors for labels of nodes
colors = ['skyblue', 'tomato', 'orange', 'purple', 'green', 'yellow', 'pink', 'red']
# 绘制以某个节点为根节点的二叉树
def print_node(node, node_tag):
# 节点颜色
color = sample(colors,1)[0]
if node.left is not None:
left_tag = str(uuid.uuid1()) # 左节点的数据
self.dot.node(left_tag, str(node.left.data), style='filled', color=color) # 左节点
label_string = 'L' if label else '' # 是否在连接线上写上标签,表明为左子树
self.dot.edge(node_tag, left_tag, label=label_string) # 左节点与其父节点的连线
print_node(node.left, left_tag)
if node.right is not None:
right_tag = str(uuid.uuid1())
self.dot.node(right_tag, str(node.right.data), style='filled', color=color)
label_string = 'R' if label else '' # 是否在连接线上写上标签,表明为右子树
self.dot.edge(node_tag, right_tag, label=label_string)
print_node(node.right, right_tag)
# 如果树非空
if self.data is not None:
root_tag = str(uuid.uuid1()) # 根节点标签
self.dot.node(root_tag, str(self.data), style='filled', color=sample(colors,1)[0]) # 创建根节点
print_node(self, root_tag)
self.dot.render(save_path) # 保存文件为指定文件
在上述代码中,笔者创建了二叉树类BTree,实现了如下方法:
初始化方法:该树存放的数据为data,左子树,右子树为left和right,默认均为None;
preorder()方法:递归实现二叉树的先序遍历;
inorder()方法:递归实现二叉树的中序遍历;
postorder()方法:递归实现二叉树的后序遍历;
levelorder()方法:递归实现二叉树的层序遍历;
height()方法:计算二叉树的高度;
leaves()方法:计算二叉树的叶子结点;
print_tree()方法:利用Graphviz实现二叉树的可视化,需要设置的参数为save_path和label,save_path为文件保存路径,默认的保存路径为当前路径下的Binary_Tree.gv,可以用户自己设置;label为是否在Graphviz文件中添加二叉树的左右子树的标签,用于分清哪棵是左子树,哪棵是右子树,可以用用户自己设置。
若我们需要实现图3的示例二叉树,完整的Python代码如下:
from Binary_Tree import BTree
# 构造二叉树, BOTTOM-UP METHOD
right_tree = BTree(6)
right_tree.left = BTree(2)
right_tree.right = BTree(4)
left_tree = BTree(5)
left_tree.left = BTree(1)
left_tree.right = BTree(3)
tree = BTree(11)
tree.left = left_tree
tree.right = right_tree
left_tree = BTree(7)
left_tree.left = BTree(3)
left_tree.right = BTree(4)
right_tree = tree # 增加新的变量
tree = BTree(18)
tree.left = left_tree
tree.right = right_tree
print('先序遍历为:')
tree.preorder()
print()
print('中序遍历为:')
tree.inorder()
print()
print('后序遍历为:')
tree.postorder()
print()
print('层序遍历为:')
level_order = tree.levelorder()
print(level_order)
print()
height = tree.height()
print('树的高度为%s.' % height)
print('叶子节点为:')
tree.leaves()
print()
# 利用Graphviz进行二叉树的可视化
tree.print_tree(save_path='E://BTree.gv', label=True)
OK,当我们运行上述代码时,可以得到该二叉树的一些信息,输出结果如下:
先序遍历为:
18 7 3 4 11 5 1 3 6 2 4
中序遍历为:
3 7 4 18 1 5 3 11 2 6 4
后序遍历为:
3 4 7 1 3 5 2 4 6 11 18
层序遍历为:
[[18], [7, 11], [3, 4, 5, 6], [1, 3, 2, 4]]
树的高度为4.
叶子节点为:
3 4 1 3 2 4
该Python代码的优势在于利用Graphviz实现了二叉树的可视化,可以形象直观地得到二叉树的图形。在上面的代码中,我们可以看到,构建二叉树不是很方便,需要手动地一个个结点去添加。那么,如果当我们需要根据某个列表,按列表顺序去构建二叉树时,即二叉树的层序遍历为该列表,那又该怎么办呢?有什么好的办法吗?
答案是必须有!按照某个列表去构建二叉树的完整Python代码如下:
from Binary_Tree import BTree
# 利用列表构造二叉树
# 列表中至少有一个元素
def create_BTree_By_List(array):
i = 1
# 将原数组拆成层次遍历的数组,每一项都储存这一层所有的节点的数据
level_order = []
sum = 1
while sum < len(array):
level_order.append(array[i-1:2*i-1])
i *= 2
sum += i
level_order.append(array[i-1:])
# print(level_order)
# BTree_list: 这一层所有的节点组成的列表
# forword_level: 上一层节点的数据组成的列表
def Create_BTree_One_Step_Up(BTree_list, forword_level):
new_BTree_list = []
i = 0
for elem in forword_level:
root = BTree(elem)
if 2*i < len(BTree_list):
root.left = BTree_list[2*i]
if 2*i+1 < len(BTree_list):
root.right = BTree_list[2*i+1]
new_BTree_list.append(root)
i += 1
return new_BTree_list
# 如果只有一个节点
if len(level_order) == 1:
return BTree(level_order[0][0])
else: # 二叉树的层数大于1
# 创建最后一层的节点列表
BTree_list = [BTree(elem) for elem in level_order[-1]]
# 从下往上,逐层创建二叉树
for i in range(len(level_order)-2, -1, -1):
BTree_list = Create_BTree_One_Step_Up(BTree_list, level_order[i])
return BTree_list[0]
#array = list(range(1,19))
array = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
tree = create_BTree_By_List(array)
print('先序遍历为:')
tree.preorder()
print()
height = tree.height()
print('\n树的高度为%s.\n'%height)
print('层序遍历为:')
level_order = tree.levelorder()
print(level_order)
print()
print('叶子节点为:')
tree.leaves()
print()
# 利用Graphviz进行二叉树的可视化
tree.print_tree(save_path='E://create_btree_by_list.gv', label=True)
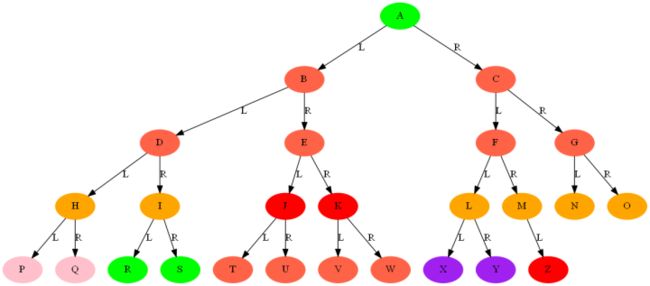
在上述程序中,笔者利用create_BTree_By_List()函数实现了按照某个列表去构建二叉树,输入的参数array为列表,要求列表中至少有一个元素。运行上述程序,我们得到的26个大写字母列表所构建的二叉树的图像如下:
输出的结果如下:
先序遍历为:
A B D H P Q I R S E J T U K V W C F L X Y M Z G N O
树的高度为5.
层序遍历为:
[['A'], ['B', 'C'], ['D', 'E', 'F', 'G'], ['H', 'I', 'J', 'K', 'L', 'M', 'N', 'O'], ['P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']]
叶子节点为:
P Q R S T U V W X Y Z N O
总结
二叉树是很多重要算法及模型的基础,比如二叉搜索树(BST),哈夫曼树(Huffman Tree),CART决策树等。本文先介绍了树的基本术语,二叉树的定义与性质及遍历、储存,然后笔者自己用Python实现了二叉树的上述方法,笔者代码的最大亮点在于实现了二叉树的可视化,这个功能是激动人心的。
在Python中,已有别人实现好的二叉树的模块,它是binarytree模块,其官方文档的网址为:https://pypi.org/project/binarytree/ 。其使用的例子如下: