一、简化的科学与科学的简化
经典物理学的问题甚至是力学问题,都并非是绝大多数人想象的那样清晰简洁。所以由自然科学探索活动所产生的一系列方法,我们决不应该未经方法论分析,不加思索地将其移植到其他领域加以应用。我们一直以来的一个错觉就是物理学致力于解释整个大自然,其实并非如此。事实上,物理学的巨大成功源于其有限的目标:揭示物体行为的规律。抛开一个宏大的目标,划定一个具体的范围,这样来解释一般的现象,才是我们通常所采取的方法。实际上指定可解释的范围,这也许是物理学对人类解决问题的方法论最了不起的发现。比如在英文中,法律和规律都是一个law字。法律只是规定了特定情况下的行为,而不能试图规定所有的行为;同样,对于研究对象,物理定律也只能确定它们在某些明确定义条件下的行为,对其他情况则未予确定。
要从一般系统的角度理解科学,我们应该审视物理学,特别是机械力学,因为其他科学常常将这些科学作为标准。在机械论的模型下力学世界之美堪称典范:机械论意味着整体完全等于部分之和,反之亦然;不论部分进行多少次分解组合,也不论按照什么样的顺序进行分解组合,整体的行为始终不变。这意味着各个部分不会给彼此带来巨大的改变,也不会因其自身的历史而发生巨大的变化。任何部分在适当的时间到达适当的位置后,就会留在那里,继续完成它完全而唯一确定的行为。这种模型的描述其实是并非精当的,因为力学系统一般由几个不同的部分组成,通常是两个,有时是十个或以上,在高度约束的情况下或许多达30个或40个,如桥梁的部件。如果部件太多,物理学家也许能写出描述不同部件行为的方程,但却不能求解,即便采用近似方法也不行。高速计算机的出现拓展了力学系统近似求解的范围,但进步不大。既然正式的力学方法有如此的局限性,为什么它被视为所有科学的典范?要得到答案,我们必须忽略正式的方法,转而去考虑非正式的方法。人们总是通过非正式的方法简化复杂力学系统,然后才开始应用正式的方法。
以牛顿对太阳系中物体运动的解释为例。我们现在知道太阳系有成千上万个天体以及其他没有成型的物质,可是所有关于行星运动的分析,从一开始就忽略了其中大部分天体。人们认为它们“太小”不足以影响计算结果。这种做法似乎很自然,以至于很多书本对此都没有提及,但实际上只有在很特殊的情况下才能这样做。所有其他情况的系统,都被认为不适用力学原理。例如,松果体在大脑中是一个体积和质量都很微小的一个存在,在试图理解人体的行为时,没有哪个生理学家会由于松果体的质量比大脑的质量小很多就可以忽略它;活细胞中的DNA只占细胞质量的很小一部分,但是如果忽略了它就可不能理解细胞生物学;蜂王只是在蜂箱中的几千只蜜蜂之一,论质量只占其中的很小一部分,但任何动物行为学家都不能够以其质量占比而忽略它。所以,力学研究的系统,仅仅是力学近似能够成功应用的系统。机械论的模型、模式及其方法,能够适用于机械力学,是因为它可以忽略一些细节而忽略了一些细节,从而也导致了它的适用范围非常有限。
我们现在讨论一下最普通的两物体系统的描述方程。首先必须描述每个物体自身的行为即“孤立的”行为;其次考虑两者的行为如何彼此影响即“相互作用”;最后考虑两个物体都不存在时系统的行为,即“场”方程。总的来说,最普通的两体系统需要4个方程:两个“孤立”方程,一个“相互作用”方程,再加一个“场”方程。随着系统中物体数量的增加,“相互作用”方程的数量则迅速增加,N个物体就需要2的N次方个相互作用方程。比如说由10个物体组成的系统就存在2的10次方=1024个方程,一万个物体的相互作用方程数量将是天文数字。求解这些方程需要付出多少成本,有多大的可行性?在牛顿时代连最小的计算机都没有,他们如何度量所需的计算量呢?经验表明,除非能够进行某种简化,否则计算量的增长至少是方程数增长的平方。这就是“计算量的平方律”。即如果方程数加倍,必须采用比时间流逝快4倍的计算机才能在相同的时间内求解。牛顿时代没有计算机,可计算量的实际上限远低于一千个二阶微分方程,况且那个时候牛顿才刚刚发明微分方程。利用所有的显式和隐式简化假设,牛顿才能侥幸成功。就这一点而言,如今我们会注意到老一辈物理学家常说:现在的年轻人不再研究“真正的物理学”了。这些年轻的“暴发户”用计算机来求解大量的方程,而不是利用物理模型的直觉先减少方程的数量,以便在所谓的信封背面用铅笔演算出结果。
想一想实际的计算如何操作实施,我们就会对力学或任何一门科学有新的认识,因为实际的计算操作实施要求把那些隐性假设明确化。力学中常常这样假设:只有某些相互作用是重要的。比如在考虑太阳系问题时,唯一重要的相互作用是万有引力,这意味着每一对关系只给出一个方程。我们怎么知道在这个系统中只有万有引力才是重要的呢?我们怎么知道可以忽略磁效应、电场力、光压力、人格魅力以及其他因素呢?我们的回答是:如果其他作用力也重要,这个问题就不是一个力学问题了。显然这种回答就是要回避问题。至于是不是一个力学问题,取决于如果我们尝试这样的近似,就能得到满意的结果,即结果符合观察数据。假如不符合这样的结果,它就不会被写入力学课本中了。这种困惑的一个实际计算例子是回声卫星的轨道计算问题,该卫星是一个膨胀且巨大的聚酯薄膜球体。在预测它的轨道时,引力方程的经典答案不能令人满意。经过艰苦努力,程序员意识到,由于它的密度很小,体积就比同样质量的太阳系天体大得多。因此照射到它表面的太阳光的压力就不能忽略,这与计算其他“普通”轨道不一样。力学本身不会告诉我们,什么系统是力学系统。
其实,即便已经使用了大量的隐性假设,使得方程个数已经减少到一千以下,问题也并没有得到解决。因为即使采用大型计算机,还是很难求解这些方程。更进一步的简化仍然是必须的。牛顿在万有引力定律中提供了一种重要的简化方式,这一定律被誉为“迄今为止人类最了不起的归纳”。万有引力定律指出,两个质点之间的相互吸引力由下式表示:F=GMm/R²
其中,M与m分别为两个质点的质量,R为两者之间的距离,G为普适常数。从简化的角度来看,这个方程说得比较隐晦:它意味着不需要其他方程。比如它实际上是在声称:两个物体之间的作用力在任何时候都与第三者无关,所以只需要考虑两两之间的作用力,然后所有这些效果可以叠加。这种简化如果能拿给其他学科适用的话,比如说心理学,研究一个三口之家的行为。那么心理学家就开心死了。这种简化意味着他只需研究夫妻行为、父子行为和母子行为,然后把三种相互行为加起来,就能预测全家的行为了。遗憾的是,只有在力学和其他少数学科中这样的两两作用叠加关系才能够适用。
在太阳系的例子中,通过两两作用的叠加,一千个方程减少到45个左右,这是从十个物体中任取两个的所有可能组合。从计算上看,我们至少已经把计算量大致减少为原来的百分之一。但牛顿的简化努力并没有就此停步,也许是因为他没有计算机的缘故。恰巧,太阳系中太阳的质量比其他物体大得多。由于这个缘故,那些没有太阳参与的两两之间的相互作用力就小得足以忽略了,至少对于牛顿想要解释的数据精度而言确实如此(简化计算结果的偏差至少让人们发现了一颗牛顿不知道的行星)。这种简化之所以可行是因为太阳系的特点,而不是因为力学原理。这样,方程数由45个减少到了10个左右,计算量也因此减少到不足原计算量的1/20。牛顿的研究甚至更进了一步。他注意到,由于太阳独一无二的巨大质量,可以将每个行星与太阳看成一个系统,与其他系统分离开来。这样分离的系统只剩下两个物体。将一个系统分解成没有相互作用的若干子系统,这对于系统理论学很重要。要理解这种分解的重要性,只需想想“计算量的平方律”:若求解一个含n个方程的系统需要2ⁿ次计算,而计算n个仅含1个方程的独立系统却只需要进行n次计算即可。
直到这时,牛顿才停止简化,开始求解方程。事实上,他还做了许多其他假设,比如把太阳系中的每个天体看成一个质点。在这些简化中,牛顿及其同时代的人通常更容易意识到简化假定,也更关心简化假定。今天讲授牛顿计算的物理学教师们则根本不关心简化的假定。所以现在的学生很难理解牛顿关于行星轨道的计算为什么能够跻身于人类最伟大的成就之列。但是,一般系统论的思想家就能够理解,因为他们所选择的任务就是理解科学的简化假设。用维格纳的话说,这些“感兴趣的对象”和“明确定义的条件”限定了科学的应用范围,增强了它的预测能力。一般系统哲思者希望从科学家对世界建模这一过程的起点入手,并依照这个过程进行下去,最终获得关于其他科学的有用模型。为什么一般系统的方法论会对科学的简化以及简化的科学如此重视?理由与牛顿完全一样,“计算量的平方律”决定了任何计算设备都有计算能力的极限。人的大脑在某种意义上也是一种计算设备。所以,如果我们想在如此复杂的世界中生存,就必须获得所有可能得到的帮助。牛顿是一个天才,不是因为他的大脑具有超级计算能力,相反是因为他会简化和理想化,使得普通人的大脑能在一定程度上认知这个世界。通过研究过去成功与失败的简化方法,我们希望人类知识的进步不要过分依赖天才。
简化与抽象,是构建认识世界模型的重要思维方法和步骤,将与研究对象关系不大的噪音屏蔽出去,留下有效信息。绘画的过程也是画家对现实建模的过程,将触动了自己的印象勾勒出来,将想要表达的美感强调出来,其他能省略的就省略掉,能概括地就概括一下。从这个意义上说,简化也是一种抽象,抽象也是一种简化。二者的本质是一致的。如果简化与抽象搞得不好,或是不到位或是过分,都可能造成一个极其丑陋的扭曲的虚假的完全失真的模型。比如新古典的主流的尤其是凯恩斯主义的经济学学说,就是这样一种怪物。纯粹的自然的经济系统在这种笨拙的“画家”笔下,被画成一个女人装扮的张飞,它所告诉人们的就是:市场是一个需要政府为之整容的丑陋女人。当然,如果需要的话,还要限制她的行动与出入。
二、不可解析或统计的“中数”世界
牛顿的成就在于他描述了一个约10⁵个物体组成的系统的行为,并从中找出感兴趣的10个物体。但一个瓶中的气体分子组成的系统就与太阳系极为不同。气体系统的组成成员是分子,瓶子中的分子数量达到10²³这个量级,而且分子的质量几乎相同并且相互之间的作用频繁、密切。尽管19世纪的物理学家已经从牛顿所开创的方法中,学会只关心物体两两之间的作用,但这也只不过是把方程数量从2的10²³次方个减少到10⁴⁶个。这种简化从数量上来说效果不可谓不显著,但对解决问题来说仍然是毫无意义的:10⁴⁶个近乎天文数字的方程是无法求解的,这种方法路子显然是笨拙无望的死胡同。研究气体系统的物理学家们只得放弃牛顿的路子另辟蹊径,他们的做法是将研究对象聚焦于某一范围的分子平均特性,而不是具体分子的个性。这种抽象的简化完全卸下了计算量的负担。而且这些诸如体积、温度、压力的可测量平均值,理论预测精度很高,因为分子数量特别大,满足“大数定律”的适用条件。所谓大数定律就是说:观测样本的数量越多,观测值越接近于预测的平均值。
大数定律更精确的表述就是薛定谔的“N的平方根定律”:物理及物理化学规律并非绝对准确,其相对误差的数量级为1/√n,其中n为共同体现出这些规律的分子个数。也就是说,研究对象必须具有相当大的数量规律才能够成立。因为相互作用的粒子数太少,“规律”的误差就很大。误差与总数呈平方根关系,比如说100万个分子数的理论预测值其误差是1‰。一百万的个数与千分之一的误差,对于规律来说,这是一个勉强的最低的门槛。当我们放弃了以个体为研究对象的路子,转为以巨量同质个数为研究对象来求取平均值,这就意味着机械力学的方法不再适用,我们必须考察所要研究的对象系统是否迈过了这个门槛,是否在求取宏观均值的统计学方法范围之内。那么,统计学方法的适用范围是什么?那就是:研究的对象数量不仅是十分巨大的,而且要求基本同质,整个对象系统的任何一部分都不能够体现出任何特殊的性质来。简明地说就是研究对象全体的行为要有足够的随机性,才可以进行统计性研究。
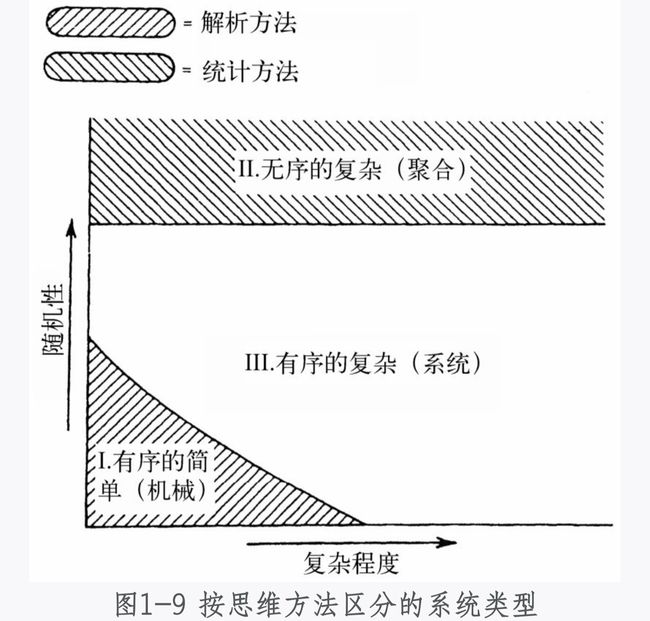
在泛系统思维中随机性是十分重要的概念,随机性是确保统计学方法适用的系统性质。让我们来通过一个统计学例子来说明,假如某地正在流行感冒,我们想知道流感的传播规律以便计划分发疫苗。如果每个人被传染的机会均等,我们就可以相当精确地预测发病数量,并计算出接种疫苗的预期效果。但如果人群中存在某种非随机性,计算就会偏离实际的情况。非随机性可能源自何处呢?比如乡村中人们的住所分布不是随机的,即每个人接触传染源的机会不一样。现在我们已经十分清楚,对于目标对象数量少的系统,我们希望它是机械力学系统,使用牛顿的力学解析方法,力求简化以降低系统的复杂程度;而对于目标对象数量庞大的系统,我们则希望它是无序的简单聚合体,力求它的同质、同构的随机性。机械技术都是得自于机械力学方法,通过减少相互关联的部件而降低复杂性。管理技术得益于统计学的成果,将人看成是无结构的群体之中可互换的单元,以求取宏观平均值。
对介于小数和大数两极之间的系统,以上两种经典的方法都存在着严格狭隘的适用前提。一方面,计算量的平方定律指出,不能用解析的方法求解中等数量对象的系统;另一方面,精确度的平方根定律又限制了百万数量以下的对象系统使用统计方法。这样一来,对于不大不小不多不少的所谓“中数”系统,可以得知对它既无法解析,也无法统计。在我们所面对的自然客体世界和社会人文世界中,理想的机械力学系统和统计学系统很少,放眼望去大都是所谓“中数”系统。计算机的部件个数是中数,细胞中酶的数量是中数,组织机构里的人数是中数,环境中的树木花鸟鱼虫的数量也是中数……我们既熟悉这样的系统,又对它们无可奈何,转换成我们的日常经验,“中数规律”就变成了墨菲定律:凡是可能发生的,都会发生。
科学的成果是简单的成果,或更恰当地说是适当地简化的成果。比如工程师必须遵循力求避免零部件之间产生过多的互动的原则,才能将少数的零部件组合成大机器;人的行动学也是力求将人看成是以自我为中心的自主个体,才能够演绎出在纯粹经济环境下的人性及其偏好规律。科学在其选定的领域内取得了巨大成功,这让很多不明觉厉又懒于求真的人误以为一种科学方法像一把万能的锤子,可以适用于它所能遇到的全部钉子。但事实上任何一种方法并不能有效地处理所有的系统。换句话说,并不存在“科学方法”这种事物,适用的方法才是科学的方法,在哪里适用就在哪里科学,在哪里不适用就在哪里不科学。我们必须要对不经检视、不加思索的技术手段的局限性,审慎地重视起来,因为这些方法不是压制中数系统成为机械力学系统,就是降低大数系统界限使用统计学方法。而不经论证就使用某些方法的经济学说,不可能成为经济科学。
在分析事物的组成部分或组成个体的特性时,人们总是倾向于夸大那些孤立时的明显的独立性,而忽略组合体、聚合体或复合体所具有的本质上的整体性和变异的个性。我们将躯体分解成各个器官,将骨架分解成骨骼;将自然科学分成了物理和化学……人类的技术已经将这种“功能分解”发挥到了极致。似乎分解已经是牢不可破的真理,是正确性无可置疑的科学方法。但分解的思维方法说穿了其实只是为了便于人们克服自身能力的不足,并不具有“放之四海而皆准”的正确性和适用性。在高精尖的技术实践中,已经有人意识到,某个设备不仅仅是部件的组合,更是部件与部件间连接关系的组合,所以人们才能够创造出更高功能水平的设备比如集成电路。生物学、社会学和经济学都不像物理学那样“成功”,它们不能随意将眼前的世界分解成小块,因为它们面对的研究对象是不可分割的。解剖学尽管非常成功,但我们对人被分解后的行为不感兴趣,社会学和经济学的主要兴趣是具有中数系统特性的人性规律,如果系统或被分解、或被过度抽象,或被平均化,人的特性和社会经济系统的特性就不复存在。经济学如果试图通过平均化来理解“个体”,个体的特性就会被分摊殆尽;而如果试图分离出个体进行研究,又割断了研究对象与其他人或世界其他部分的联系,个体仅仅成为实验室的人造物,而不再是人。
我们应该警惕把系统看成部件的组合、把个体看成对平均值的贡献所带来的后果。也许我们已接近科学和技术有用性的极限,因为科学技术的哲学基础是局限于小数系统和大数系统的技术。当然,任何方法的适用性超出其范围都不是科学的,一般系统方法也不例外。一般系统方法不是要得到对中数系统的绝对控制,它的主要贡献很可能是限制对复杂系统不适当地、过度地应用其他方法。要想改变人类科学历史百多年来的偏颇和执迷这一趋势,我们仍然不得不采用更多的综合方法。