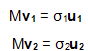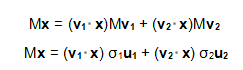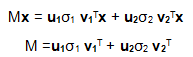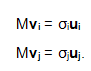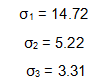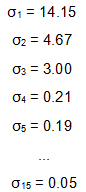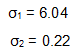PS:一直以来对SVD分解似懂非懂,此文为译文,原文以细致的分析+大量的可视化图形演示了SVD的几何意义。能在有限的篇幅把这个问题讲解的如此清晰,实属不易。原文举了一个简单的图像处理问题,简单形象,真心希望路过的各路朋友能从不同的角度阐述下自己对SVD实际意义的理解,比如 个性化推荐中应用了SVD,文本以及Web挖掘的时候也经常会用到SVD。
SVD目的:奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性。就像是描述一个人一样,给别人描述说这个人长得浓眉大眼,方脸,络腮胡,而且带个黑框的眼镜,这样寥寥的几个特征,就让别人脑海里面就有一个较为清楚的认识,实际上,人脸上的特征是有着无数种的,之所以能这么描述,是因为人天生就有着非常好的抽取重要特征的能力,让机器学会抽取重要的特征,SVD是一个重要的方法。
英文原文:We recommend a singular value decomposition
简介
SVD实际上是数学专业内容,但它现在已经渗入到不同的领域中。SVD的过程不是很好理解,因为它不够直观,但它对矩阵分解的效果却非常好。比如,Netflix(一个提供在线电影租赁的公司)曾经就悬赏100万美金,如果谁能提高它的电影推荐系统评分预测准确率提高10%的话。令人惊讶的是,这个目标充满了挑战,来自世界各地的团队运用了各种不同的技术。最终的获胜队伍"BellKor's Pragmatic Chaos"采用的核心算法就是基于SVD。
SVD提供了一种非常便捷的矩阵分解方式,能够发现数据中十分有意思的潜在模式。在这篇文章中,我们将会提供对SVD几何上的理解和一些简单的应用实例。
线性变换的几何意义(The geometry of linear transformations)
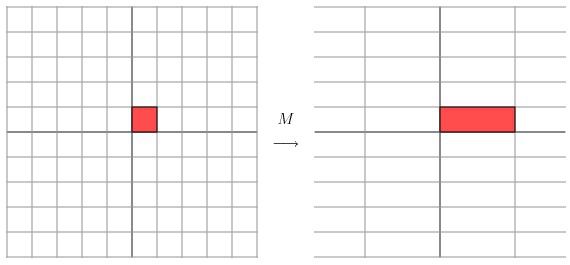
让我们来看一些简单的线性变换例子,以2 X 2的线性变换矩阵为例,首先来看一个较为特殊的,对角矩阵:
从几何上讲,M是将二维平面上的点(x,y)经过线性变换到另外一个点的变换矩阵,如下图所示
变换的效果如下图所示,变换后的平面仅仅是沿X水平方面进行了拉伸3倍,垂直方向是并没有发生变化。
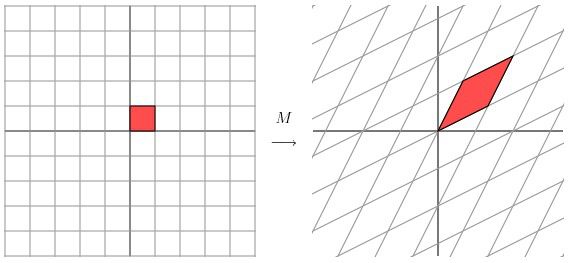
现在看下矩阵
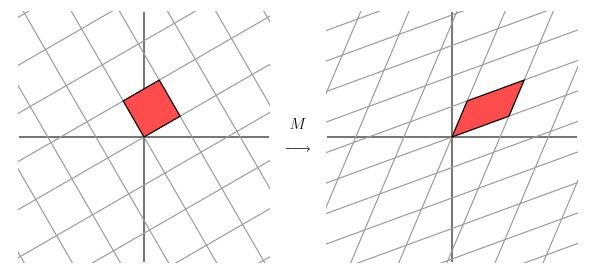
这个矩阵产生的变换效果如下图所示
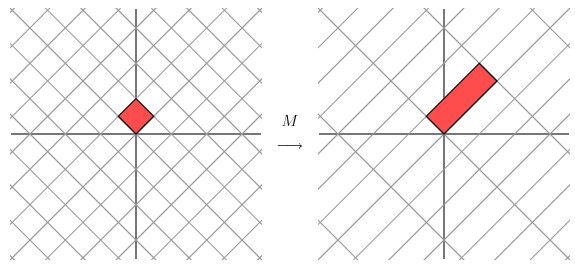
这种变换效果看起来非常的奇怪,在实际环境下很难描述出来变换的规律(这里应该是指无法清晰辨识出旋转的角度,拉伸的倍数之类的信息)。还是基于上面的对称矩阵,假设我们把左边的平面旋转45度角,然后再进行矩阵M的线性变换,效果如下图所示:
看起来是不是有点熟悉?对的,经过M线性变换后,跟前面的对角矩阵的功能是相同的,都是将网格沿着一个方向拉伸了3倍。
这里的M是一个特例,因为它是对称的。非特殊的就是我们在实际应用中经常遇见一些 非对称的,非方阵的矩阵。如上图所示,如果我们有一个2 X 2的对称矩阵M的话,我们先将网格平面旋转一定的角度,M的变换效果就是在两个维度上进行拉伸变换了。
用更加数学的方式进行表示的话,给定一个对称矩阵M,我们可以找到一些相互正交Vi,满足MVi就是沿着Vi方向的拉伸变换,公式如下:
这里的λi是拉伸尺度(scalar)。从几何上看,M对向量Vi进行了拉伸,映射变换。Vi称作矩阵M的特征向量(eigenvector),λi称作为矩阵M特征值(eigenvalue)。这里有一个非常重要的定理,对称矩阵M的特征向量是相互正交的。
如果我们用这些特征向量对网格平面进行线性变换的话,再通过M矩阵对网格平面进行线性换的效果跟对M矩阵的特征向量进行线性变换的效果是一样的。
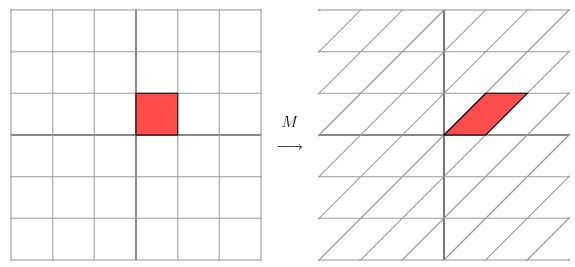
对于更为普通的矩阵而言,我们该怎么做才能让一个原来就是相互垂直的网格平面(orthogonal grid),线性变换成另外一个网格平面同样垂直呢?PS:这里的垂直如图所示,就是两根交错的线条是垂直的。
经过上述矩阵变换以后的效果如图
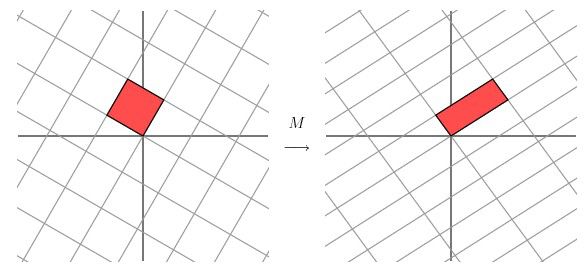
从图中可以看出,并没有达到我们想要的效果。我们把网格平面旋转30度角的话,然后再进行同样的线性变换以后的效果,如下图所示
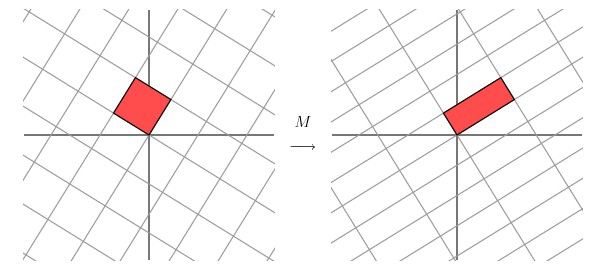
让我们来看下网格平面旋转60度角的时候的效果。
嗯嗯,这个看起来挺不错的样子。如果在精确一点的话,应该把网格平面旋转58.28度才能达到理想的效果。
几何意义
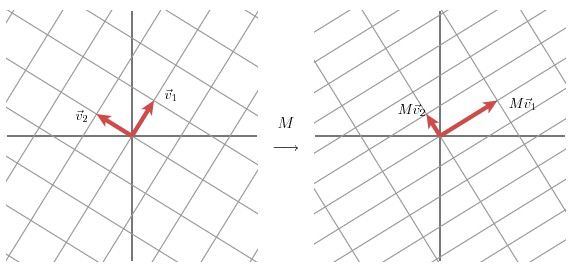
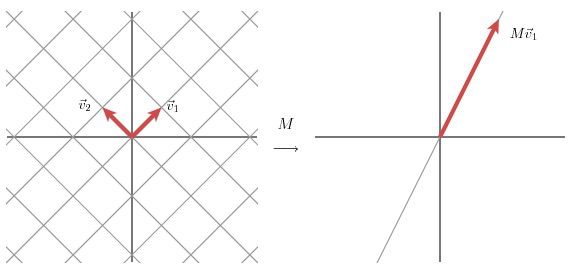
该部分是从几何层面上去理解二维的SVD:对于任意的2 x 2矩阵,通过SVD可以将一个相互垂直的网格(orthogonal grid)变换到另外一个相互垂直的网格。
我们可以通过向量的方式来描述这个事实:首先,选择两个相互正交的单位向量v1和v2,向量Mv1和Mv2正交。
u1和u2分别表示Mv1和Mv2的单位向量,σ1*u1=Mv1和σ2*u2=Mv2。σ1和σ2分别表示这不同方向向量上的模,也称作为矩阵M的奇异值。
这样我们就有了如下关系式
我们现在可以简单描述下经过M线性变换后的向量x的表达形式。由于向量v1和v2是正交的单位向量,我们可以得到如下式子:
这就意味着:
向量内积可以用向量的转置来表示,如下所示
最终的式子为
上述的式子经常表示成
u矩阵的列向量分别是u1,u2,Σ是一个对角矩阵,对角元素分别是对应的σ1和σ2,V矩阵的列向量分别是v1,v2。上角标T表示矩阵V的转置。
这就表明任意的矩阵M是可以分解成三个矩阵。V表示了原始域的标准正交基,u表示经过M变换后的co-domain的标准正交基,Σ表示了V中的向量与u中相对应向量之间的关系。(V describes an orthonormal basis in the domain, and U describes an orthonormal basis in the co-domain, and Σ describes how much the vectors in V are stretched to give the vectors in U.)
如何获得奇异值分解?( How do we find the singular decomposition? )
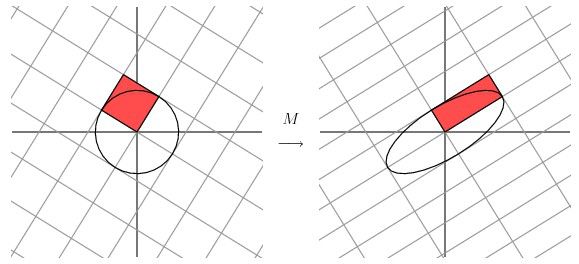
事实上我们可以找到任何矩阵的奇异值分解,那么我们是如何做到的呢?假设在原始域中有一个单位圆,如下图所示。经过M矩阵变换以后在co-domain中单位圆会变成一个椭圆,它的长轴(Mv1)和短轴(Mv2)分别对应转换后的两个标准正交向量,也是在椭圆范围内最长和最短的两个向量。
换句话说,定义在单位圆上的函数|Mx|分别在v1和v2方向上取得最大和最小值。这样我们就把寻找矩阵的奇异值分解过程缩小到了优化函数|Mx|上了。结果发现(具体的推到过程这里就不详细介绍了)这个函数取得最优值的向量分别是矩阵MT M的特征向量。由于MTM是对称矩阵,因此不同特征值对应的特征向量都是互相正交的,我们用vi表示MTM的所有特征向量。奇异值σi= |Mvi|, 向量ui为Mvi方向上的单位向量。但为什么ui也是正交的呢?
推倒如下:
σi和σj分别是不同两个奇异值
另一方面,我们有
因此,ui和uj是正交的。但实际上,这并非是求解奇异值的方法,效率会非常低。这里也主要不是讨论如何求解奇异值,为了演示方便,采用的都是二阶矩阵。
应用实例(Another example)
现在我们来看几个实例。
实例一
经过这个矩阵变换后的效果如下图所示
在这个例子中,第二个奇异值为0,因此经过变换后只有一个方向上有表达。
换句话说,如果某些奇异值非常小的话,其相对应的几项就可以不同出现在矩阵M的分解式中。因此,我们可以看到矩阵M的秩的大小等于非零奇异值的个数。
实例二
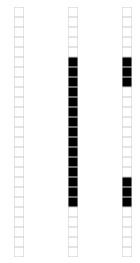
我们来看一个奇异值分解在数据表达上的应用。假设我们有如下的一张15 x 25的图像数据。
如图所示,该图像主要由下面三部分构成。
我们将图像表示成15 x 25的矩阵,矩阵的元素对应着图像的不同像素,如果像素是白色的话,就取1,黑色的就取0.我们得到了一个具有375个元素的矩阵,如下图所示
如果我们对矩阵M进行奇异值分解以后,得到奇异值分别是
实例三
减噪(noise reduction)
前面的例子的奇异值都不为零,或者都还算比较大,下面我们来探索一下拥有零或者非常小的奇异值的情况。通常来讲,大的奇异值对应的部分会包含更多的信息。比如,我们有一张扫描的,带有噪声的图像,如下图所示
我们采用跟实例二相同的处理方式处理该扫描图像。得到图像矩阵的奇异值:
很明显,前面三个奇异值远远比后面的奇异值要大,这样矩阵M的分解方式就可以如下:
经过奇异值分解后,我们得到了一张降噪后的图像。
实例四
数据分析(data analysis)
我们搜集的数据中总是存在噪声:无论采用的设备多精密,方法有多好,总是会存在一些误差的。如果你们还记得上文提到的,大的奇异值对应了矩阵中的主要信息的话,运用SVD进行数据分析,提取其中的主要部分的话,还是相当合理的。
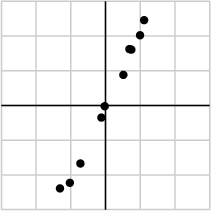
作为例子,假如我们搜集的数据如下所示:
我们将数据用矩阵的形式表示:
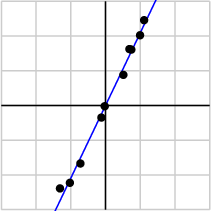
经过奇异值分解后,得到
由于第一个奇异值远比第二个要大,数据中有包含一些噪声,第二个奇异值在原始矩阵分解相对应的部分可以忽略。经过SVD分解后,保留了主要样本点如图所示
就保留主要样本数据来看,该过程跟PCA( principal component analysis)技术有一些联系,PCA也使用了SVD去检测数据间依赖和冗余信息.
总结(Summary)
这篇文章非常的清晰的讲解了SVD的几何意义,不仅从数学的角度,还联系了几个应用实例形象的论述了SVD是如何发现数据中主要信息的。在netflix prize中许多团队都运用了矩阵分解的技术,该技术就来源于SVD的分解思想,矩阵分解算是SVD的变形,但思想还是一致的。之前算是能够运用矩阵分解技术于个性化推荐系统中,但理解起来不够直观,阅读原文后醍醐灌顶,我想就从SVD能够发现数据中的主要信息的思路,就几个方面去思考下如何利用数据中所蕴含的潜在关系去探索个性化推荐系统。也希望路过的各位大侠不吝分享呀。
References:
Gilbert Strang,Linear Algebra and Its Applications. Brooks Cole
William H. Presset al,Numercial Recipes in C: The Art of Scientific Computing. Cambridge University Press.
Dan Kalman,A Singularly Valuable Decomposition: The SVD of a Matrix,The College Mathematics Journal27(1996), 2-23.
If You Liked This, You're Sure to Love That,The New York Times, November 21, 2008.