生活中,我们可能遇到这样的情况,朋友小明向你借10000元,保证5个月连本带息还给你。假设你手上有如下两套方案:
| 方案1 | 方案2
----|----|---
第一月还款|3350 | 2100
第二月还款|3050 | 2100
第三月还款|2000 | 2100
第四月还款|1000 | 2100
第五月还款|1000 | 2100
总还款|10400 | 10500
如果单看收益/利息的话,毫无疑问应该选择方案2。那是否真的就是方案2更好?或者说如果某个方案更好,它相当于另一个方案好多少,能否量化?回答这个问题就需要用到IRR的知识。
IRR( internal rate of return)内部收益率,是一种投资的评估方法,也就是找出资产潜在的回报率,其原理是利用内部回报率折现,投资的净现值恰好等于零。其求解公式如下:
其中n代表回合(案例中N=5),Cn代表收益,C0为初始投资金额(为负数,如方案1,C0=-10000,C1=3350...),r就是需要求解的IRR。公式可以看出是一个一元多次方程,我们知道五次及五次以上的代数方程一般不能用根式求解。如果要求解这个方程的根就需要用到超越方程求解方法。
Newton's method
牛顿法(Newton's method)又称为牛顿-拉弗森方法(Newton-Raphson method),它是一种在实数域和复数域上近似求解方程的方法。
公式如下:
使用牛顿法,我们需要初始一个x0,尽可能贴近要求解的根。这个时候这个方程会收敛(Newton's method只具有局部收敛性),当达到我们精度要求,就可以得到解。对于我们要解的IRR,应该是位于(-1,1]之间的值,我们的x0也就可以选择这其中的数字进行迭代。
我的实现代码如下:
long double f(long double x)
{
long double out = 0;
for (int i = 0; i <= M; i++) {
if (i == 0) {
out -= c[i] * powl(x, M);
}
else
{
out += c[i] * powl(x, M-i);
}
}
return out;
}
long double derf(long double x)
{
long double out = 0;
for (int i = 0; i < M; i++) {
if (i == 0) {
out -= c[i] * powl(x, M-1) * M;
}
else
{
out += c[i] * powl(x, M-i-1) * (M - 1);
}
}
return out;
}
long double NewtonRaphson(long double factor)
{
long double up = f(factor), down = derf(factor);
return factor - up / down;
}
调用的代码:
long double pre = 1.618;
long double now = NewtonRaphson(pre);
while (fabsl(now-pre) > precision * fabsl(now)) {
if (fabsl(now) < precision) {
break;
}
pre = now;
now = NewtonRaphson(pre);
}
其中precision就是精度,设置的是1e-9,最后如果能找到结果,那么now-1就是IRR。Newton's method可以解决一部分超越方程求根问题,但是某些方程在Newton's method下会呈现不收敛情况,就不能用这种方法。
Bisection method
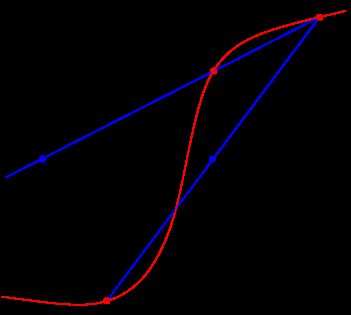
二分法(英语:Bisection method),是一种方程式的近似值求法,也可以用来求已知范围的超越方程的解。IRR正好就是求解区间(-1,1]的值,所以可以使用Bisection method。
求解流程如下:
若要求已知函数 f(x) = 0 的根 (x 的解),则:
- 先找出一个区间 [a, b],使得f(a)与f(b)异号。根据介值定理,这个区间内一定包含着方程式的根。
- 求该区间的中点m=(a+b)/2,并找出 f(m) 的值。
- 若 f(m) 与 f(a) 正负号相同则取 [m, b] 为新的区间, 否则取 [a, m]。
- 重复第2和第3步至理想精确度为止。
我的实现代码如下:
long double f(long double x)
{
long double out = 0;
for (int i = 0; i <= M; i++) {
if (i == 0) {
out -= c[i] * powl(x, M);
}
else
{
out += c[i] * powl(x, M-i);
}
}
return out;
}
long double biSearch()
{
long double left = precision, right = 2;
while (fabsl(right - left) > precision) {
long double mid = (right + left) / 2.0;
long double fmid = f(mid),fleft = f(left);
if (fmid * fleft > 0) {
left = mid;
}
else
{
right = mid;
}
}
return right;
}
这里left初始并没有取0,是为了防止取到IRR=-1而抛弃了其他更有意义的值。
Secant method
在数值分析中,割线法(Secant method)是一个求根算法,该方法用一系列割线的根来近似代替函数f的根。他和牛顿的算法思想相似,但实现方式不同,这种方法同样也有不收敛的情况。
公式如下:
从上式中可以看出,割线法需要两个初始值x0和x1,它们离函数的根越近越好。
我的实现代码如下:
long double f(long double x)
{
long double out = 0;
for (int i = 0; i <= M; i++) {
if (i == 0) {
out -= c[i] * powl(x, M);
}
else
{
out += c[i] * powl(x, M-i);
}
}
return out;
}
long double secant()
{
long double first = precision, second = 2;
while (fabsl(second - first) > precision) {
long double f1 = f(first),f2 = f(second);
long double next = second - f2 * (second - first) / (f2 - f1);
first = second;
second = next;
}
return second;
}
Microsoft Excel中求解IRR的公式就是用的这个算法,Excel中的精度是0.00001%。
Regula Falsi method
这种算法是针对前面Secant Method和Newton Method算法可能出现不收敛情况而提出的,它一定会收敛,并且相对于Bisection Method效率更高。
他的思想是在交换逼近方向的时候用一个系数(这里选2)去调整取值。公式如下(如果系数由1/2变为1,公式就和Secant Method一样):
与
我的实现代码如下:
long double f(long double x)
{
long double out = 0;
for (int i = 0; i <= M; i++) {
if (i == 0) {
out -= c[i] * powl(x, M);
}
else
{
out += c[i] * powl(x, M-i);
}
}
return out;
}
long double Falsi()
{
long double left = precision, right = 2;
int side = 0;
long double fleft = f(left), fright = f(right);
long double ratio = (fleft*right - fright *left) / (fleft - fright);
while (fabsl(right - left) > precision) {
ratio = (fleft*right - fright *left) / (fleft - fright);
long double fratio = f(ratio);
if (fright * fratio > 0) {
right = ratio;
fright = fratio;
if (side == -1) {
fleft /= 2;
}
side = -1;
}
else if (fleft * fratio > 0)
{
left = ratio;
fleft = fratio;
if (side == 1) {
fright /= 2;
}
side = 1;
}
else
{
break;
}
}
return ratio;
}
现在有了超越方程的解法与IRR的概念,那么对于小明的借款,到底哪种方案对于自己更好呢?
下面看一下两种方案Excel计算结果:
可以看到方案1的IRR=1.69%,方案2的IRR=1.65%。方案1的虽然总利息少了,但是内部收益率更高。所以对于作为东家的自己来说选择方案1更优。
不仅限于上面的案例,类似的对于房贷还款,银行提供了等额本金与等额本息两种方式。客户往往倾向于等额本金方式,因为还款总利息更少。那么对于银行来说到底哪种方式对于他们来说更优?有了IRR和超越方程知识,我们也可以自己算一下。