Lecture 8 Normalization and Affymetrix

原文地址：http://x2yline.gitee.io/microarray_data_analysis_note/notes/8%20Normalization%20and%20Affymetrix/8%20Normalization%20and%20Affymetrix.html

1. 什么是标准化

广义：为了使不同芯片的数据具有可比性

狭义：使芯片的均值（中位数）相等

系统误差来源

提取的RNA总量不同

RNA提取，逆转录，荧光标记，PCR扩增等各个环节的效率

DNA的质量

变异会掩盖真正有差异的基因

2. 标准化方法

方法1：管家基因法

选择一组认为表达量不会变化的基因，并根据这几个基因对芯片进行校正

缺点：不知道哪些是表达量不变的基因，不能保证这些基因在处理过程或癌变过程中表达不发生变化

关于管家基因的定义：通常认为对细胞的生命功能具有重要作用，表达恒定并且通常表达量比较高的基因；另一个不同的定义是不同情况下该基因的表达在不同芯片中的rank相同，选出这些基因并以他们为参考进行标准化。

方法2：spike-ins外加合成序列法

引入一些能控制相对密度的标志序列及探针，并使用这些探针对剩余的探针进行标准化

缺点：不知道如何控制标志序列与样品的相对量

方法3：简单缩放进行标准化

通过乘以一个标准化系数，从而使不同芯片的数据的分布及均值大致相同，，从而使其具有可比性

缺点：不能保证MA plot为一条水平直线（可能有弯曲），如何确定标准化系数（是使用RNA总信号强度，中位数还是其他的值？）

其他方法

同时使用spike-ins和简单缩放进行标准化，spike-ins包括很多不同强度的值，并用它们来检验缩放后的值是否可信

基线

当我谈论变异时，通常是以某个芯片作为基线即参考的，dChip算法是以表达值处于中位数的某个芯片为参考的

使用一组表达量不变的探针，并在不同信号强度区域使用不同的scale factor进行校正，该校正通是在两个芯片之间进行的，该方法与在MA plot中拟和一条光滑曲线，把M值与该曲线相减得到校正数据的方法相同。

前提条件

通过缩放使90%的基因表达量具有可比性是否在当两个样本的基因表达模式有很大差异时合理

缩放即百分位数法对芯片数据进行校正的前提条件是大多数基因的表达是没有发生变化的，百分位数法对该假设的依赖性比缩放法更强，当这个假设不成立时，使用上述方法进行标准化是没有意义的

大多数基因表达量不发生变化的情况有：

饱食/饥饿实验
热休克实验
对比不同器官（？？？）

3. 如何评价不同的标准化方法

接下来的内容基本上来自于Bolstad, Irizarry, Astrand 和 Speed（bekerley的文章 Bioinformatics, 2003, p.185-193

对于在生物学上认为表达相同的基因，在经过标准后之后表达应该是基本相等的

3.1 测试标准化方法的数据集

Affymetrix 拉丁方设计实验数据

The Affymetrix Latin Square Experiment (Hu95Av2, repeated on Hu133A)，该数据集是合成的已知浓度序列，并按照拉丁方实验设计进行芯片实验。

其中U95Av2芯片共有14组合成的序列，每组序列的浓度分别为： 0, 0.25, 0.5, 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, and 1024 pM，至少重复三次后，每组合成序列的对应浓度向前移位，如第二个实验中每组序列的浓度从 0.25 pM 开始并以 0 pM结尾，共59个芯片。每组合成序列大多都是只含有一种序列，但组1含有2种序列，组12是空白组。

Hu 133A芯片共42个芯片，有14组实验，每组实验重复3次，共42个合成序列这些序列浓度范围为0.125 pM 到 512 pM，与U95 数据不同，该数据集包含更多合成序列，从更小的浓度开始，扫描仪器为GeneChip™ Scanner 3000，更少探针与序列交叉杂交的情况。

Gene Logic Dilution Data

75个Hu95Av2芯片，两个组织来源：肝脏和中枢神经系统，其中包括；

每种组织各自30个芯片
- 5种不同浓度，每个浓度重复6次
剩下的15个芯片是两种组织的混合样本
- 3中不同比例的样品（27:75, 50:50, 75:25），各自重复5次

4个·肝脏组织的芯片数据在Bioconductor的包affydata的内置数据Dilution中

library(affydata)
data("Dilution")

pData(Dilution)
##     liver sn19 scanner
## 20A    20    0       1
## 20B    20    0       2
## 10A    10    0       1
## 10B    10    0       2

varMetadata(phenoData(Dilution))
##                                                               labelDescription
## liver                    amount of liver RNA hybridized to array in micrograms
## sn19    amount of central nervous system RNA hybridized to array in micrograms
## scanner                                              ID number of scanner used

A Gene Logic Spike In Dataset

98个 Hu95Av1芯片，共11 cRNA个合成序列，其中26个芯片所有合成序列浓度相同，但不同芯片的浓度不同（芯片1浓度都为0，芯片2浓度都为0.5，芯片3浓度都为0.75），剩下的芯片组成两个拉丁方设计，每个水平3个重复。

我们需要用到的数据是Dulition使用的5个肝脏样本的数据（所有样本都在同一个稀释水平）

26个Gene Logic Spike In数据集的芯片，单个芯片上所有合成序列浓度相同

为什么Gene Logic公司做该实验并提供数据，因为Gene Logic是最大的Affy芯片消费者之一，他们收集了非常多表达谱数据并进行销售；他们想提高数据分析的质量并为他们自己的方法打广告，该数据可以在官网申请。

3.2 标准化验证

标准化的方法共有：

library(affydata)
normalize.AffyBatch.methods()
## [1] "constant"         "contrasts"        "invariantset"     "loess"           
## [5] "methods"          "qspline"          "quantiles"        "quantiles.robust"

3.2.1 基线方法

选择一个芯片作为基线（中位数）对所有芯片进行缩放（affy的算法是在汇总定量后使用该方法，但是这里我们使用探针水平的数据进行缩放）
Nonlinear invariant rank方法进行标准化，同样选择一个芯片作为基线

3.2.2 Complete Data方法（不需要选择基线）

Cyclic Loess（循环loess拟合）
Contrasts
Quantiles（分位数法）

Cyclic Loess方法

$$
M_{k} = log{2}(x{ki}/x{kj})
$$

i，j代表芯片编号，若$\hat{M_{k}}$为拟合的曲线，校正后的M值应该是
$$
M_{k}'=M_{k}-\hat{M_{k}}
$$
那么我们如何来校正每个芯片的值呢？该方法使用对称校正的方法
$$
x'{ki} = 2^{A{k}+0.5\bullet M'_{k}}
$$

$$
x'{ki} = 2^{A{k}-0.5\bullet M'_{k}}
$$

对所有芯片都进行校正，通常需要重复2~3次，但是该方法运行速度较慢（n个芯片计算的时间复杂度至少是O(n^2)）

Contrast Based Normalization

详细算法可见该文章：Contrast Normalization of Oligonucleotide Arrays

最开始的输入是一个n*k的矩阵，n代表features数，k代表芯片编号，该矩阵已经经过log2转化
乘以正交对比矩阵（线性代数的知识）后，转化后的第一列是所有芯片表达矩阵的均值（相当MA plot相对于x-y plot的旋转使曲线水平化）
再对除第一列以外的其他列进行曲线拟合，并校正除第一列以外的其他列（使均值为0），再进行矩阵逆运算得到校正后的表达矩阵

点评：该算法最主要的思想是对log密度值根据均值进行缩放（几何均值）

比Cyclic Loess方法快，但计算速度仍较慢

Quantile分位数法

该方法的前提假设为每个芯片的表达数据分布都是完全相同的

n个芯片p个探针组成一个p * n的矩阵X
对矩阵X的每一列分别进行排序，使每一行的表达量值在相应每一列的分位数都相同
计算每一行的均值，并替代原值，使得该矩阵同一行的数据完全相同
把每一列的数据位置还原，形成校正后的表达矩阵

该方法值涉及排序和做均值，计算速度极快

为什么选择均值作为新的表达量值？

当我们以两个芯片的表达量值分别作为x和y轴即做y-x plot时，如果两个样本所有基因的分位数都相同，则形成一条完美的对角直线（y=x）

实际上，我们做的y-x plot越靠近y=x说明标准化效果越好，而需要对n个芯片两两作图，这提示使用均值作为新的表达量值

使用均值作为新的表达量，我们不需要考虑缩放的问题，并且结果显示对于对数化的数据和原始数据标准化效果都比较好，但是二者计算出来的新表达量值不同

我们更倾向于使用中位数而不是均值，是否进行对数转化不影响最终的标准化的值，虽然取均值和中位数时大部分差异并不的

3.2.3 选择不同基线的影响

不同基线的选择最后得出的表达值差异可能非常大

3.2.4 如何定义标准化是否成功

我们想要的结果是各个芯片数据的分布大致相同，从而具有可比性，评价标准化是否成功最常用的就是MA plot

为了使之前的预处理相同，所有芯片的预处理均使用同一种方法，如RMA方法处理背景信号

文章的一些结果

通常MA plot在标准化之前的直线有一定的曲率，这提示标准化过程需用曲线进行拟合，否则不使用非线性方法进行标准化
所有结果均显示标准化之后的原始数据显示出更小的变异性
使用complete data方法比baseline chip方法结果更好，对于simple constant scaling比非线性方法如invariant rank set更好
三种complete data方法中，结果相差不大，quantile方法结果稍微更好，并且因为quantile方法的速度明显比其他的快，因此他们推荐使用quantile方法

4. 如何进行标准化

首选要确认是否大部分基因的表达量没有发生很大的改变

接着我们可以检验一下MA plot是否是水平的，如果是水平的我们就不需要使用quantiles方法进行标准化

如果MA plot不是水平的，我们再检验一下芯片的质量（图片）是否有人为的异常，如果没有异常则可以使用quantiles方法处理

4.1 一次Bioconductor的冒险

我们的目标：重复文献Bolstad et al. (2003)的研究，使用Bioconductor提供的数据

首选载入数据和函数

library(affy)
library(affydata)
data(Dilution)

以一个AffyBatch对象即Dilution数据开始（把CEL文件读入创建的数据），我们想测试不同标准化方法的效率及准确性

预测处理步骤包括：

Background correction
Normalization
PM correction
Summary Quantification

4.2 是否需要标准化

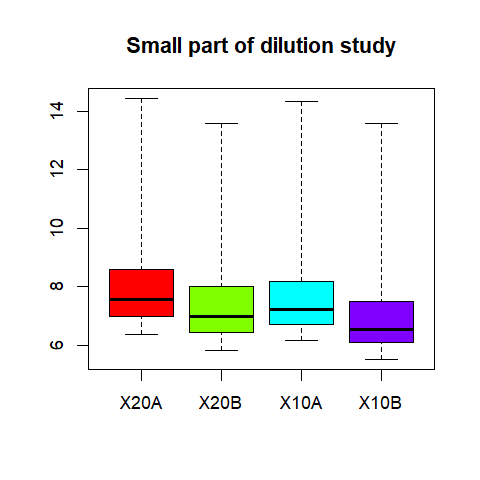
# shows log intensities!
boxplot(Dilution, col=rainbow(4))

dev.copy(png,file="boxplot1.png")
dev.off()

Lecture 8 Normalization and Affymetrix_第1张图片

分布密度图

hist(Dilution,lty=1,col=rainbow(4),lwd=3, main="intensity distribution")

dev.copy(png,file="hist1.png", res=108)
dev.off()

[]http://x2yline.gitee.io/microarray_data_analysis_note/notes/8%20Normalization%20and%20Affymetrix/assets/hist1.png)

MA plot（有参考基线）

par(mfrow=c(2,2))
MAplot(Dilution)
par(mfrow=c(1,1))

dev.copy(png,file="MAplot1.png", res=72)
dev.off()

Lecture 8 Normalization and Affymetrix_第2张图片

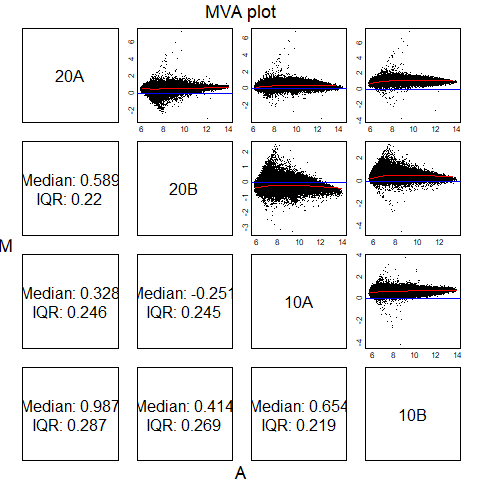
MA plot（相互比较）

mva.pairs(Dilution)
## Error in log(new("AffyBatch", cdfName = "HG_U95Av2", nrow = 640L, ncol = 640L,  :  unused argument (2)

help(mva.pairs)
# a matrix containing the chip data in the columns.

提取AffyBatch对象为矩阵之后才能使用mva.pairs函数，如果记不住证明提取数据矩阵，可以查看AffyBatch的slot

slotNames(Dilution)
##  [1] "cdfName"           "nrow"              "ncol"              "assayData"        
##  [5] "phenoData"         "featureData"       "experimentData"    "annotation"       
##  [9] "protocolData"      ".__classVersion__"

Dilution@cdfName
## [1] "HG_U95Av2"

Dilution@nrow
## [1] 640

Dilution@ncol
## [1] 640

Dilution@phenoData
## An object of class 'AnnotatedDataFrame'
##   sampleNames: 20A 20B 10A 10B
##   varLabels: liver sn19 scanner
##   varMetadata: labelDescription

Dilution@experimentData
## Experiment data
##   Experimenter name: Gene Logic 
##   Laboratory: Gene Logic 
##   Contact information: 708 Quince Orchard Road
## Gaithersburg, MD 20878
## Telephone: 1.301.987.1700
## Toll Free: 1.800.GENELOGIC (US and Canada)
## Facsimile: 1.301.987.1701
##  
##   Title: Small part of dilution study 
##   URL: http://qolotus02.genelogic.com/datasets.nsf/ 
##   PMIDs:  
## 
##   Abstract: A 68 word abstract is available. Use 'abstract' method.
##   notes:
##    :     
## 

Dilution@annotation
## [1] "hgu95av2"

Dilution@.__classVersion__
##         R   Biobase      eSet AffyBatch 
##  "2.10.0"   "2.5.5"   "1.3.0"   "1.2.0"

而其中的assayData和phenoData可以用了提取数据矩阵和样本信息

Dilution@assayData
## $exprs
##            20A     20B     10A     10B
## 1        149.0   112.0   129.0    60.0
## 2       1153.5   575.3  1262.3   564.8
## ...
## 250      118.0    93.0   117.8    69.0
##  [ reached getOption("max.print") -- omitted 409350 rows ]

class(Dilution@assayData)
## [1] "list"

length(Dilution@assayData)
## [1] 1

names(Dilution@assayData)
## [1] "exprs"

class(Dilution@assayData[[1]])
## [1] "matrix"

dim(Dilution@assayData[[1]])
## [1] 409600      4

样本信息可以用以下命令

Dilution@phenoData
## An object of class 'AnnotatedDataFrame'
##   sampleNames: 20A 20B 10A 10B
##   varLabels: liver sn19 scanner
##   varMetadata: labelDescription

class(Dilution@phenoData)
## [1] "AnnotatedDataFrame"
## attr(,"package")
## [1] "Biobase"

slotNames(Dilution@phenoData)
## [1] "varMetadata"       "data"              "dimLabels"         ".__classVersion__"

Dilution@phenoData@data
##     liver sn19 scanner
## 20A    20    0       1
## 20B    20    0       2
## 10A    10    0       1
## 10B    10    0       2

Dilution@phenoData@varMetadata
##                                                               labelDescription
## liver                    amount of liver RNA hybridized to array in micrograms
## sn19    amount of central nervous system RNA hybridized to array in micrograms
## scanner

我们也可以使用exprs提取AffyBatch对象中的数据矩阵

length(exprs(Dilution))
## [1] 1638400

dim(exprs(Dilution))
## [1] 409600      4

mva.pairs(exprs(Dilution))
dev.copy(png,file="MAplot2.png", res=72)
dev.off()

Lecture 8 Normalization and Affymetrix_第3张图片

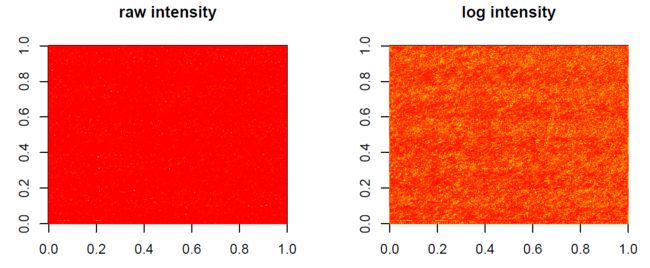
image(Dilution[,1],transfo=log2)

Lecture 8 Normalization and Affymetrix_第4张图片

放大可以看到芯片顶部有特殊标记（说明芯片没有放反）

Lecture 8 Normalization and Affymetrix_第5张图片

par(mfrow=c(1,2))
image(matrix(exprs(Dilution[,1]),
             nrow=nrow(Dilution),
             ncol=ncol(Dilution)),
      main="raw intensity")

image(log2(matrix(exprs(Dilution[,1]),
             nrow=nrow(Dilution),
             ncol=ncol(Dilution))),
      main="log intensity")

par(mfrow=c(1,1))

Lecture 8 Normalization and Affymetrix_第6张图片

可以看出MA plot的线并不是非常水平，并且图像没有明显认为误差，可以使用quantiles进步标准化

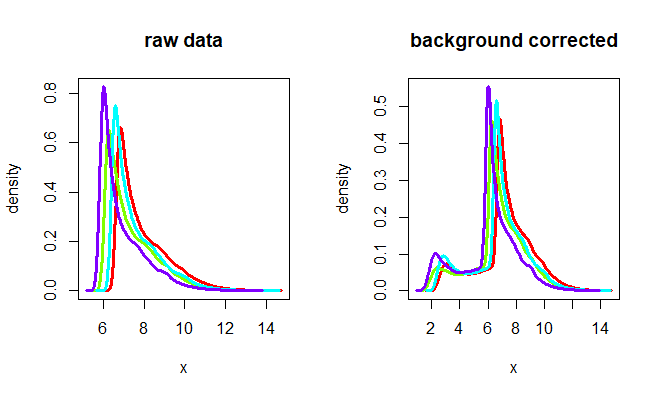
4.3 背景校正

4.3.1 使用RMA校正背景

Dilution.bg <- bg.correct.rma(Dilution)

par(mfrow=c(1, 2))
hist(Dilution, lty=1, col=rainbow(4), lwd=3,
     main="raw data")
hist(Dilution.bg, lty=1, col=rainbow(4), lwd=3,
     main="background corrected")

## hist对AffyBatch对象默认进行log2处理，并绘制PM的密度分布
## 下面的代码与上面的代码等价
plotDensity(log2(pm(Dilution)),
            lty=1, col=rainbow(4), lwd=3,
            main="raw data")
plotDensity(log2(pm(Dilution.bg)),
            lty=1, col=rainbow(4), lwd=3,
            main="background corrected")

Lecture 8 Normalization and Affymetrix_第7张图片

log2处理后的分布如下图

plotDensity(log2(exprs(Dilution)),
            lty=1, col=rainbow(4), lwd=3,
            main="raw data")
plotDensity(log2(exprs(Dilution.bg)),
            lty=1, col=rainbow(4), lwd=3,
            main="background corrected")

Lecture 8 Normalization and Affymetrix_第8张图片

4.3.2 使用MAS校正背景

par(mfrow=c(1, 2))
Dilution.bg.rma <- bg.correct.rma(Dilution)
hist(Dilution.bg.rma, lty=1, col=rainbow(4), lwd=3,
     main="RMA background corrected")

Dilution.bg.mas <- bg.correct.mas(Dilution)
hist(Dilution.bg.mas, lty=1, col=rainbow(4), lwd=3,
     main="MAS background corrected")

par(mfrow=c(1, 1))

[图片上传失败...(image-57c667-1525937569283)]

这说明不同的背景校正方法有比较大的差异，比较不同的标准化方法时，应在相同背景校正方法的情况下进行比较

4.4 标准化

标准化的方法有：

normalize.AffyBatch.constant
normalize.AffyBatch.contrasts
normalize.AffyBatch.invariantset
normalize.AffyBatch.quantiles

首选不进行标准化的结果：

eset0 <- expresso(Dilution,
                  bgcorrect.method="rma",
                  normalize=FALSE,
                  pmcorrect.method="pmonly",
                  summary.method="medianpolish")

eset0是一个ExpressionSet对象，用exprs提取的矩阵维度变小了，有原来的features(probes)变成了probesets

slotNames(eset0)
## [1] "experimentData"    "assayData"         "phenoData"         "featureData"   
## [5] "annotation"        "protocolData"      ".__classVersion__"

rownames(eset0@featureData@data)[10]
## [1] "1008_f_at"

eset0@assayData
## 

ls(eset0@assayData)
## [1] "exprs"    "se.exprs"

dim(get("exprs", eset0@assayData))
## [1] 12625     4

R中的环境：可以把R中的“pass by value”模式转化为“pass by reference”模式
myEnv <- new("environment")
frogs <- rnorm(5)
assign("frogs",frogs,envir=myEnv)
ls(myEnv)
## [1] "frogs"

得到未经标准化数据每个probset的均值和方差

dim(exprs(eset0))
## [1] 12625 4

eset0.mu <- apply(exprs(eset0),1,"mean")
eset0.var <- apply(exprs(eset0),1,"var")

寻找middle behavior芯片

apply(exprs(Dilution), 2, "median")
## 20A 20B 10A 10B 
## 188 127 149  94

constant方法与未经标准化的样本间差异比较

第三个为参考基线，用constant方法进行标准化

eset1 <- expresso(Dilution,
                  bgcorrect.method = "rma",
                  normalize.method = "constant",
                  normalize.param = list(refindex=3),
                  pmcorrect.method = "pmonly",
                  summary.method = "medianpolish")

eset1.mu <- apply(exprs(eset1),1,"mean")
eset1.var <- apply(exprs(eset1),1,"var")

MA plot对不同方法进行比较

A1 <- (eset0.mu + eset1.mu)/2

## M1是两种方法对探针均值的影响比较，不能描述哪种方法比较好
M1 <- (eset0.mu - eset1.mu)/2

## M2是两种方法对探针方差的影响比较，通常越好的方法越能减少样本之间的差异
M2 <- (eset0.var / eset1.var)
M3 <- log2(eset0.var / eset1.var)

d0 <- 0.0001;
M4 <- log2((eset0.var + d0)/(eset1.var + d0))

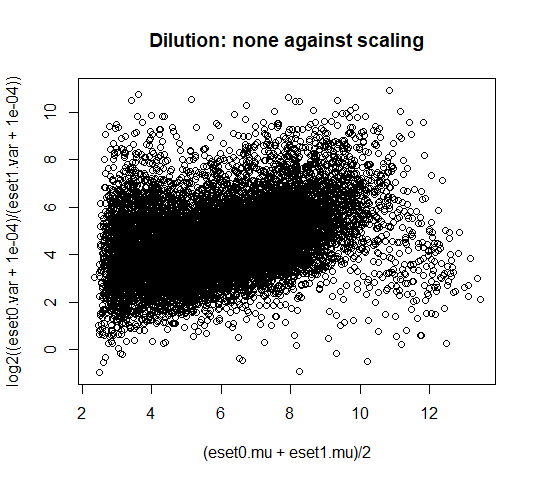
plot(A1, M4, 
     xlab="(eset0.mu + eset1.mu)/2",
     ylab="log2((eset0.var + 1e-04)/(eset1.var + 1e-04))",
     main="Dilution: none against scaling")
# 大部分点都大于0，说明constant缩放标准化减少了方差

Lecture 8 Normalization and Affymetrix_第9张图片

quantiles标准化方法与constant方法对样本间差异性的影响比较

eset2 <- expresso(Dilution,
                  bgcorrect.method="rma",
                  normalize.method="quantiles",
                  pmcorrect.method="pmonly",
                  summary.method="medianpolish")
eset2.mu <- apply(exprs(eset2),1,"mean")
eset2.var <- apply(exprs(eset2),1,"var")

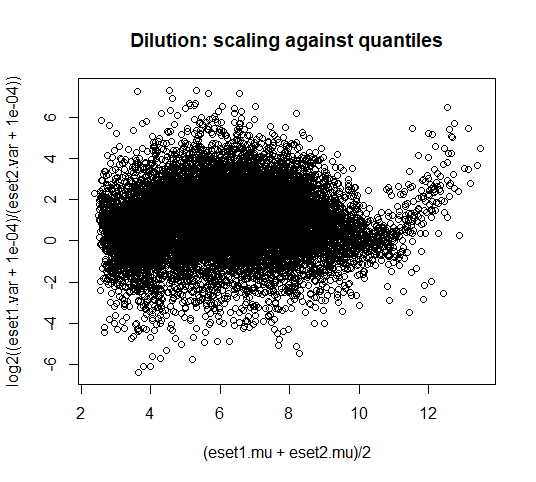
plot((eset1.mu+eset2.mu)/2,
     log2((eset1.var + 1e-04)/(eset2.var + 1e-04)),
     main="Dilution: scaling against quantiles")
# 大部分点都大于0，均值为0.98，说明quantiles方法比constant方法更能缩小样本间的差异

Lecture 8 Normalization and Affymetrix_第10张图片

改变背景校正方法为mas

以上我们比较的是不同标准化方法对样本之间的差异性的影响，通常该差异性也受不同背景校正方法和汇总法的影响，在上述比较中，我们使用的是rma进行背景校正，汇总方法是median polish方法，接下来我们使用mas进行背景校正，median polish进行汇总，得到的比较结果如下

eset0 <- expresso(Dilution,
                  bgcorrect.method="mas",
                  normalize=FALSE,
                  pmcorrect.method="pmonly",
                  summary.method="medianpolish")

eset0.mu <- apply(exprs(eset0),1,"mean")
eset0.var <- apply(exprs(eset0),1,"var")

eset1 <- expresso(Dilution,
                  bgcorrect.method = "mas",
                  normalize.method = "constant",
                  normalize.param = list(refindex=3),
                  pmcorrect.method = "pmonly",
                  summary.method = "medianpolish")

eset1.mu <- apply(exprs(eset1),1,"mean")
eset1.var <- apply(exprs(eset1),1,"var")

eset2 <- expresso(Dilution,
                  bgcorrect.method="mas",
                  normalize.method="quantiles",
                  pmcorrect.method="pmonly",
                  summary.method="medianpolish")
eset2.mu <- apply(exprs(eset2),1,"mean")
eset2.var <- apply(exprs(eset2),1,"var")

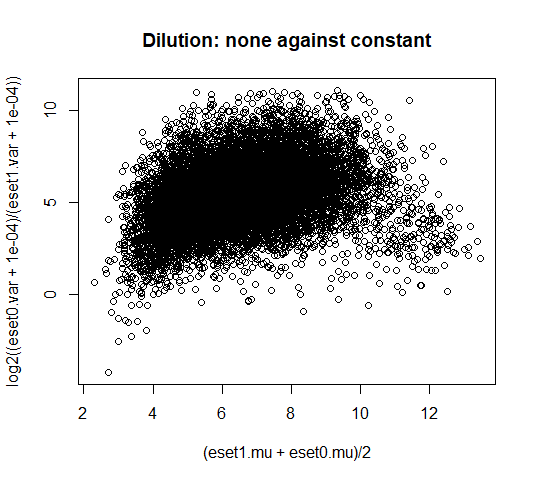
plot((eset1.mu+eset0.mu)/2,
     log2((eset0.var + 1e-04)/(eset1.var + 1e-04)),
     main="Dilution: none against constant")
# 大部分点都大于0，说明constant缩放标准化减少了方差

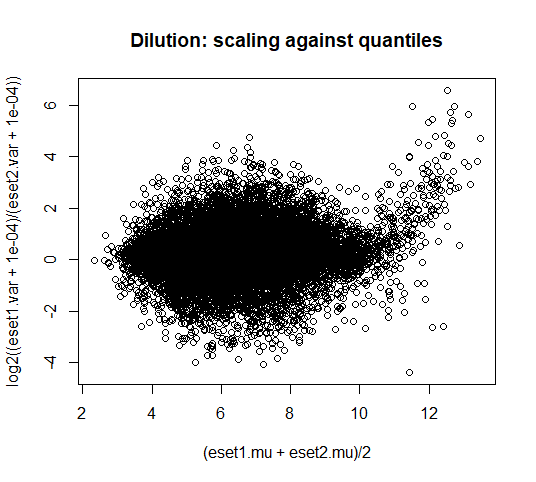
plot((eset1.mu+eset2.mu)/2,
     log2((eset1.var + 1e-04)/(eset2.var + 1e-04)),
     main="Dilution: scaling against quantiles")
# 大部分点都大于0，均值为0.265，说明quantiles方法比constant方法更能缩小样本间的差异

Lecture 8 Normalization and Affymetrix_第11张图片

Lecture 8 Normalization and Affymetrix_第12张图片

Bioconductor还有一个R包affycomp能很方便对不同方法进行比较