R语言-方差分析

方差分析指的是不同变量之间互相影响从而导致结果的变化

1.单因素方差分析:

　　案例:50名患者接受降低胆固醇治疗的药物,其中三种治疗条件使用药物相同(20mg一天一次,10mg一天两次,5mg一天四次),剩下的两种方式是(drugE和drugD),代表候选药物

　　　　 哪种药物治疗降低胆固醇的最多?

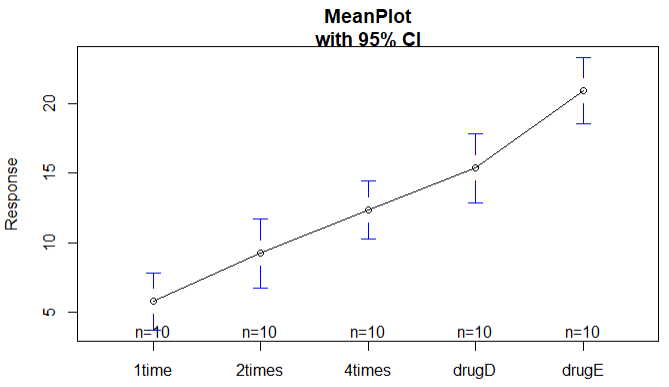
 1 library(multcomp)
 2 attach(cholesterol)
 3 # 1.各组样本大小
 4 table(trt)
 5 # 2.各组均值
 6 aggregate(response,by=list(trt),FUN=mean)
 7 # 3.各组标准差
 8 aggregate(response,by=list(trt),FUN=sd)
 9 # 4.检验组间差异
10 fit <- aov(response ~ trt)
11 summary(fit)
12 library(gplots)
13 # 5.绘制各组均值和置信区间
14 plotmeans(response ~ trt,xlab = 'Treatment',ylab = 'Response',main='MeanPlot\nwith 95% CI')
15 detach(cholesterol)

　　结论:

　　　　1.均值显示drugE降低胆固醇最多,1time降低胆固醇最少.

　　　　2.说明不同疗法之间的差异很大

　　多重比较药品和服药次数

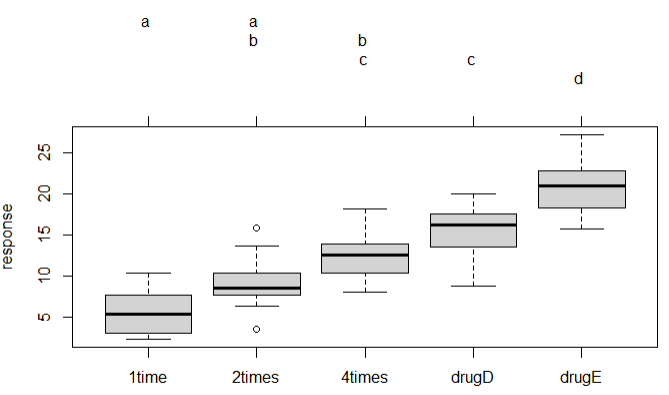
1 library(multcomp)
2 par(mar=c(5,4,6,2))
3 tuk <- glht(fit,linfct=mcp(trt='Tukey'))
4 plot(cld(tuk,level=.05),col='lightgrey')

 

　　　　结论:每天复用4次和使用drugE的时候治疗胆固醇效果最好

 　　评估检验的假设条件

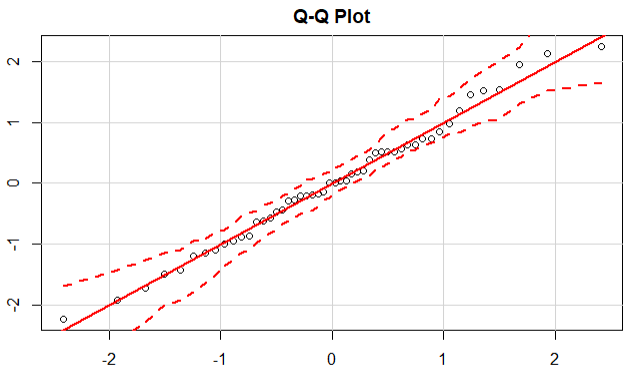
1 library(car)
2 qqPlot(lm(response ~ trt,data=cholesterol),simulate=T,main='Q-Q Plot',labels=F)
3 bartlett.test(response ~ trt,data=cholesterol)
4 # 检测离群点
5 outlierTest(fit)

　　结论:数据落在95%置信区间的范围内,说明数据点满足正态性假设

　2.单因素协方差分析

　　案例:怀孕的小鼠被分为4各小组,每个小组接受不同剂量的药物剂量(0.5,50,500)产下小鼠体重为因变量,怀孕时间为协变量

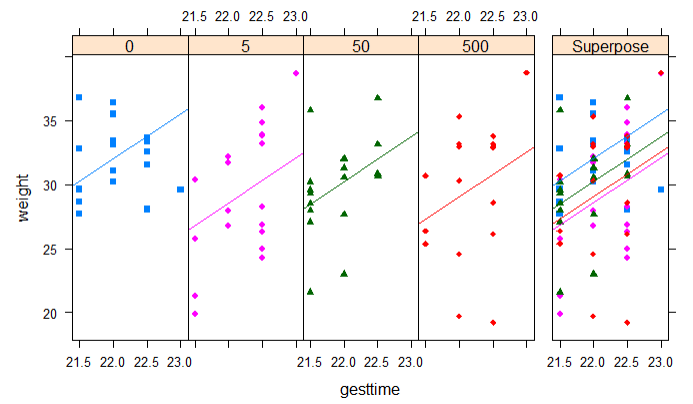
 1 data(litter,package = 'multcomp')
 2 attach(litter)
 3 table(dose)
 4 aggregate(weight,by=list(dose),FUN=mean)
 5 fit2 <- aov(weight ~ gesttime + dose)
 6 summary(fit2)
 7 library(effects)
 8 # 取出协变量计算调整的均值
 9 effect('dose',fit2)
10 contrast <- rbind('no drug vs drug' = c(3,-1,-1,-1))
11 summary(glht(fit2,linfct=mcp(dose=contrast)))
12 library(HH)
13 ancovaplot(weight ~ gesttime + dose,data=litter)

 

 

　结论:0剂量产仔20个,500剂量产仔17个

　　　 0剂量的体重在32左右,500剂量在30左右

　　     怀孕时间和体重相关

　　     用药剂量和体重相关

　

　　结论:小鼠的体重和怀孕时间成正比和剂量成反比

3.双因素方差分析

　　案例:随机分配60只豚鼠,分别采用两种喂食方法(橙汁或者维C),各种喂食方法中含有抗坏血酸3钟含量(0.5,1,2)

　　　　 每种处理组合都分配10只豚鼠,牙齿长度为因变量

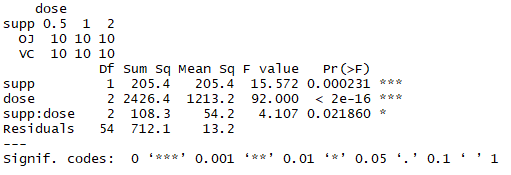
1 attach(ToothGrowth)
2 table(supp,dose)
3 aggregate(len,by=list(supp,dose),FUN=mean)
4 aggregate(len,by=list(supp,dose),FUN=sd)
5 # 将dose转换为因子变量,这样就不是一个协变量
6 dose <- factor(dose)
7 fit3 <- aov(len ~ supp*dose)
8 summary(fit3)
9 detach(ToothGrowth)

　　结论:主效应的对豚鼠牙齿影响很大

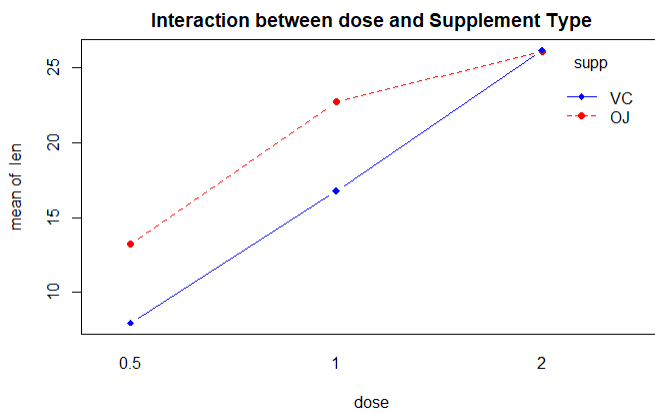
　　结论:在0.5~1mg的区间中维C的豚鼠的牙齿长度超过使用橙汁的小鼠,在1~2的区间内同理,当超过2mg时,两者对豚鼠牙齿的影响相同

4.重复测量方差

　　案例:在一定浓度的CO2的环境中比较寒带植物和非寒带植物的光合作用率进行比较

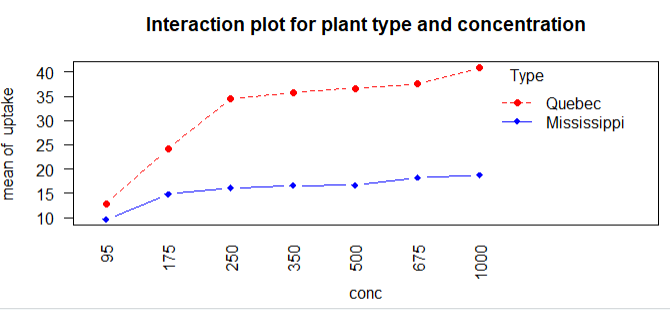
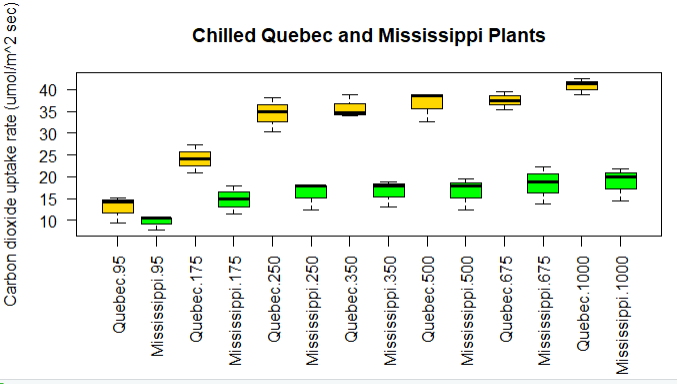
 1 CO2$conc <- factor(CO2$conc)
 2 w1b1 <- subset(CO2,Treatment == 'chilled')
 3 fit4 <- aov(uptake ~ conc*Type + Error(Plant/(conc)),w1b1)
 4 summary(fit4)
 5 par(las=2)
 6 par(mar=c(10,4,4,2))
 7 with(w1b1,interaction.plot(conc,Type,uptake,type='b',col=c('red','blue'),pch=c(16,18),
 8                            main='Interaction plot for plant type and concentration'))
 9 boxplot(uptake~Type*conc,data=w1b1,col=c('gold','green'),
10         main = 'Chilled Quebec and Mississippi Plants',
11         ylab="Carbon dioxide uptake rate (umol/m^2 sec)")

　　结论:魁北克的植物比密西西比州的二氧化碳的吸收率高,随着CO2的浓度体高,效果越明显

5.多元方差分析

　　案例:研究美国食物中的卡路里,脂肪,糖分是否会因货架的不同而不同

1 library(MASS)
2 attach(UScereal)
3 shelf <- factor(shelf)
4  y <- cbind(calories,fat,sugars)
5  aggregate(y,by=list(shelf),FUN=mean)
6  cov(y)
7  fit5 <- manova(y ~ shelf)
8  summary(fit5)
9  summary.aov(fit5)

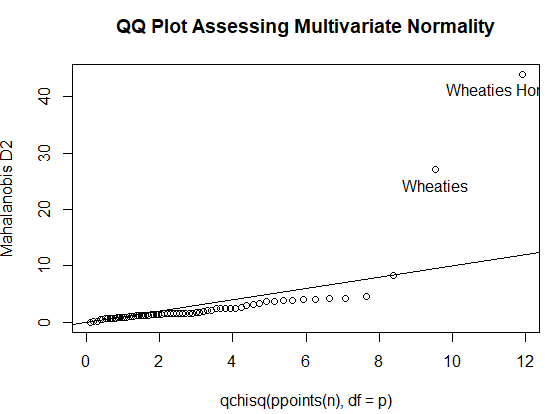
　　找出离群点

 1 center <- colMeans(y)
 2 n <- nrow(y)
 3 p <- ncol(y)
 4 cov <- cov(y)
 5 d <- mahalanobis(y,center,cov)
 6 coord <- qqplot(qchisq(ppoints(n),df=p),d,
 7                 main="QQ Plot Assessing Multivariate Normality",
 8                 ylab="Mahalanobis D2")
 9 abline(a=0,b=1)
10 identify(coord$x,coord$y,labels = row.names(UScereal))

　　结论:在不同的货架上的谷物营养成分不同,有两个产品不符合多元正态分布

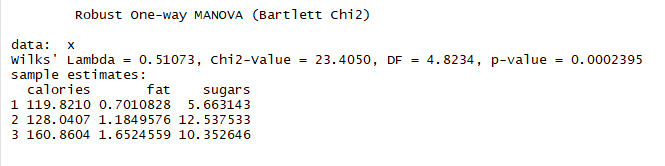
1 library(rrcov)
2 # 稳健多元方差分析
3 Wilks.test(y,shelf,method='mcd')

　

　　结论:稳健检测对离群点和违反MANOVA不敏感,证明了在不同货架的谷物营养成分不同的结论