前言:
文中有许多基础知识,在前面的博客已经进行记录,可参见–>深入浅出 KNN算法
- 概述
- 线性模型在机器学习领域是一种常见且好用的模型
- 关于线性模型,之前写过一篇介绍比较详细的博客,可以拿去看一看(英文版,可以翻译过来看)、
这是一个链接–>?
- 什么是线性模型
- 直观理解
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-5,5,100)
y = 2*x + 1
plt.plot(x,y,c='orange')
plt.title("Line")
plt.show()
- 一般公式
h(x)= w[ 0 ]*x[ 0 ] + w[ 1 ]*x[ 1 ] + … +w[ n ]*x[ n ] + b- w 叫做权重(weight)
- b 叫做偏置(bias)
- x 就是特征(features)
- 如上图,只有一个权重和偏置就是一个简单线性函数
- 在这里,一般公式可以被看作是很多个简单线性函数的加权和
- 线性模型的分类
- 线性模型主要包括一下几种:
- 线性回归
- 岭回归
- 套索回归
- 逻辑回归
- 线性SVC
- 简单入门之【两点确定一条直线】
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
X = [[1],[3]]
Y = [2,6]
line = LinearRegression()
fit = line.fit(X,Y)
z = np.linspace(0,5,20)
plt.scatter(X,Y,c='orange',s=80)
plt.plot(z,fit.predict(z.reshape(-1,1)),c='k')
plt.title("Two points determine a straight line")
plt.show()
昨天写完了KNN算法,去图书馆想找本关于爬虫的书,对于爬虫只能说会一点,但是AI是由数据驱动的科学,巧妇难为无米之炊嘛,不精通爬虫怎么拿数据。也很遗憾,没有一本和我心意,还不如看文档。又看了本《未来简史》,怎说,观点新颖,数据翔实,作者以色列人,战火连年,看待问题看得透彻的多,是个有思想的人。
又是清闲的一天。
–2019.9.7
- 简单入门之【三点确定一条直线】
- 概述
两点确定一条直线是我们大家都知道的常识,并没有看出有什么特别,事实上这条曲线是拟合出来的,为了更好的理解什么是拟合,我们用三点确定一条直线的实例更好的理解一下 - 绘图
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
X = [[1],[3],[5]]
Y = [2,8,10]
line = LinearRegression()
fit = line.fit(X,Y)
z = np.linspace(0,5,20)
plt.scatter(X,Y,c='orange',s=80)
plt.plot(z,fit.predict(z.reshape(-1,1)),c='k')
plt.title("Three points determine a straight line")
plt.show()
- 分析
我们看到,三点并不是在同一条直线上的,但是我们的算法进行了拟合,这条线是位于和三个点的距离相加最小的位置。对于两点确定一条直线的算法实际上也是一样的,只不过恰好和两个点的距离相加最小的位置就是经过两点的位置
- 获得方程
> print("y= %s x + %s "% (line.coef_[0],line.intercept_) )
y= 1.9999999999999996 x + 0.6666666666666687 //不美观
> print('y= {:.2f}'.format(line.coef_[0])+'x'+'+ {:.2f}'.format(line.intercept_))
y= 2.00x+ 0.67
- 多点拟合
- 尝试多点进行拟合
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
//唯一的区别
X,Y = make_regression(n_samples=60,n_features=1,n_informative=1,noise=50,random_state=8)
line = LinearRegression()
fit = line.fit(X,Y)
z = np.linspace(-5,5,200)
plt.scatter(X,Y,c='orange',s=60)
plt.plot(z,fit.predict(z.reshape(-1,1)),c='k')
plt.title("Three points determine a straight line")
plt.show()
print('y= {:.2f}'.format(line.coef_[0])+'x'+'+ {:.2f}'.format(line.intercept_))
- 打分
> print("模型的得分是%s"% fit.score(X,Y))
模型的得分是0.5822662968081783 //着实不高
- 小结,线性模型的特点
在【多点拟合】的实例中,我们对模型进行了打分,发现模型的得分只有0.58,这是一个很低的分数了,回想当
时我们的KNN算法,正确率可以达到96%。不过对比一下生成的图片或许就可以发现这是应该的嘛,KNN的曲线是
弯曲的尽量拟合到更多的点,线性模型是一条直线,虽然它也想照顾尽量多的点,但是心有余而力不足呐
但这并不代表线性回归比KNN要差。不知道曾记否,KNN在挑战多维度的数据时的同样表现不佳,仅仅76%的正确
率,而线性回归却可以胜任特征变量较多的情况。
这需要我们继续学习如何确定模型参数w和b,以及控制模型的复杂度
- 线性回归
- 概述
最基本的线性模型 - 原理
最小二乘法 - 实例
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
X,Y = make_regression(n_samples=150,n_features=3,n_informative=3,noise=50,random_state=8)
x0,x1,y0,y1 = train_test_split(X,Y,random_state=8)
lr = LinearRegression().fit(x0,y0)
print(lr.coef_[:]) //打印出W
print(lr.intercept_) //打印出b
//因为在此处我们的特征(features)有三个,不好用图直观的表现出来,所以通过方程系数来观察
结果
[33.88580927 90.99326451 -0.47505101]
6.459306001047711
改进
print("y = ",end=" ")
for w in lr.coef_:
i = 1
print("{:.2f}".format(float(w)) +"[X%s]"%i+" +",end=" ")
i=i+1
print("{:.2f}".format(float(lr.intercept_)),end=" ")
结果
y = 33.89[X1] + 90.99[X1] + -0.48[X1] + 6.46
//这就是我们拟合出来的线性回归方程
好几天没学习了,让弄得心烦气躁的。
滴,老年卡
–2019.9.10
打分:
print(lr.score(x1,y1)
结果:
0.8443642455178372 //还是一般,比KNN好点儿
//这是我们自己生成的数据集,用现实的数据集试试看
- 葡萄酒实例
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
import numpy as np
from sklearn.datasets import load_wine
wine = load_wine()
x0,x1,y0,y1 = train_test_split(
wine.data,wine.target,random_state=0)
lr = LinearRegression().fit(x0,y0)
print("y = ",end=" ")
for w in lr.coef_:
i = 1
print("{:.2f}".format(float(w)) +"[X%s]"%i+" +",end=" ")
i=i+1
print("{:.2f}".format(float(lr.intercept_)))
结果:
y = -0.09[X1] + 0.03[X1] + -0.09[X1] + 0.03[X1] + -0.00[X1] + 0.22[X1] + -0.47[X1] + -0.43[X1] + 0.08[X1] + 0.05[X1] + -0.12[X1] + -0.32[X1] + -0.00[X1] + 3.20
打分:
print(lr.score(x1,y1)
结果:
0.8043532631769539 //差不多( •̀ ω •́ )
- 糖尿病实例
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
import numpy as np
from sklearn.datasets import load_diabetes
diabete = load_diabetes()
x0,x1,y0,y1 = train_test_split(
diabete.data,diabete.target,random_state=0)
lr = LinearRegression().fit(x0,y0)
print("y = ",end=" ")
for w in lr.coef_:
i = 1
print("{:.2f}".format(float(w)) +"[X%s]"%i+" +",end=" ")
i=i+1
print("{:.2f}".format(float(lr.intercept_)))
结果:
y = -43.27[X1] + -208.67[X1] + 593.40[X1] + 302.90[X1] + -560.28[X1] + 261.48[X1] + -8.83[X1] + 135.94[X1] + 703.23[X1] + 28.35[X1] + 153.07
打分:
print(lr.score(x1,y1))
结果:
0.35940090989715534 //这也太低了吧
总结:
看来,我们的回归模型需要得到改进
昨天是精彩的一天,我有故事,你有酒吗?
–2019.9.11
- L1正则化线性回归–套索回归
- 正则化?
当我们使用数据进行机器学习的时候,有时候会过拟合的现象即,训练集表现很好,打分可能达到100%,但是测试集表现较差的情况,这个时候就需要正则化对数据进行处理,降低模型的复杂度,减少测试误差。
可以参考之前的一篇博客 - 原理
简单粗暴的设置某些特征的系数为0,这样会使模型得到简化,重要的特征得到突出 - 糖尿病实例
//因为线性回归模型栽在了糖尿病问题上了,所以我们就和他死磕了,这次还是用糖尿病实例
from sklearn.linear_model import Lasso
from sklearn.datasets import load_diabetes
diabete = load_diabetes()
x0,x1,y0,y1 = train_test_split(
diabete.data,diabete.target,random_state=0)
lasso = Lasso()
ls = lasso.fit(x0,y0)
print("y = ",end=" ")
for w in ls.coef_:
i = 1
print("{:.2f}".format(float(w)) +"[X%s]"%i+" +",end=" ")
i=i+1
print("{:.2f}".format(float(ls.intercept_)))
print(ls.score(x0,y0))
print(ls.score(x1,y1))
结果:
y = 0.00[X1] + -0.00[X1] + 442.68[X1] + 0.00[X1] + 0.00[X1] + 0.00[X1] + -0.00[X1] + 0.00[X1] + 330.76[X1] + 0.00[X1] + 152.52
0.41412544493966097
0.27817828862078764 //分数更低了//但我们看到的确有几项W变成了0
分析:
其实在套索回归(lasso regression)中有一个正则化参数alpha,这个参数用来控制特征变量系数约束的强度,默认值是1.0。
alpha的调节:
简单来说,alpha的值越小,正则化的效果越弱,容易出现过拟合现象,模型的泛化就越难
from sklearn.linear_model import Lasso
from sklearn.datasets import load_diabetes
diabete = load_diabetes()
x0,x1,y0,y1 = train_test_split(
diabete.data,diabete.target,random_state=0)
lasso = Lasso(alpha=0.1) //调参
ls = lasso.fit(x0,y0)
print("y = ",end=" ")
for w in ls.coef_:
i = 1
print("{:.2f}".format(float(w)) +"[X%s]"%i+" +",end=" ")
i=i+1
print("{:.2f}".format(float(ls.intercept_)))
print(ls.score(x0,y0))
print(ls.score(x1,y1))
结果:
y = -0.00[X1] + -129.78[X1] + 592.20[X1] + 240.12[X1] + -41.64[X1] + -47.63[X1] + -219.10[X1] + 0.00[X1] + 507.36[X1] + 0.00[X1] + 152.99
0.5482904661846931
0.35500225702888577 //L1正则化还不如不进行正则话呢
- 葡萄酒实例:
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_wine
from sklearn.linear_model import Lasso
wine = load_wine()
x0,x1,y0,y1 = train_test_split(
wine.data,wine.target,random_state=0)
lasso = Lasso(alpha=0.1)
ls = lasso.fit(x0,y0)
print("y = ",end=" ")
for w in ls.coef_:
i = 1
print("{:.2f}".format(float(w)) +"[X%s]"%i+" +",end=" ")
i=i+1
print("{:.2f}".format(float(ls.intercept_)))
print(ls.score(x0,y0))
print(ls.score(x1,y1))
结果:
y = -0.00[X1] + 0.00[X1] + -0.00[X1] + 0.03[X1] + 0.00[X1] + -0.00[X1] + -0.34[X1] + 0.00[X1] + -0.00[X1] + 0.09[X1] + -0.00[X1] + -0.01[X1] + -0.00[X1] + 1.37
0.8599103077552858
0.8298747376836272 //比线性回归的分数高上一些
分析:
看来,L1正则化并不是适合所有的情况
它更适合:
数据特征很多,但是只有一小部分是真正重要的。(葡萄酒实例有13个features)
接下来介绍一个更好一点的模型,岭回归.
- L2正则化线性回归–岭回归
-
原理
实际上是一种改良版的最小二乘法。它保留所有的特征,但是会减小特征变量的系数值,这样一来,特征的影响力就相对的变小了。比如说,我们通过一定的办法,把特征值限定在0~1之间,这样一来,特征对模型的影响将是很有限的。
L1正则化线性回归算是比较“正统的”的正则化思想 -
参数alpha
与套索回归一样,岭回归有个参数alphs
较高的alpha值表示对模型的限制更加严格(正则化程度高)
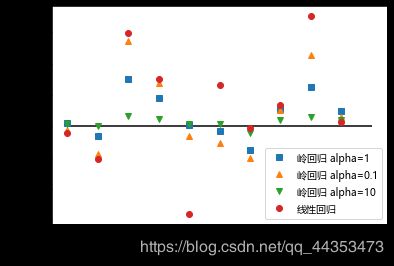
- 不同alpha值对应参数值比较:
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
from sklearn.linear_model import Lasso
from sklearn.linear_model import LinearRegression
plt.rcParams['font.sans-serif'] =['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
diabete = load_diabetes()
x0,x1,y0,y1 = train_test_split(
diabete.data,diabete.target,random_state=0)
lr = LinearRegression().fit(x0,y0)
ridge = Ridge()
ri = ridge.fit(x0,y0)
ridge = Ridge(alpha=10)
ri10 = ridge.fit(x0,y0)
ridge = Ridge(alpha=0.1)
ri01 = ridge.fit(x0,y0)
plt.plot(ri.coef_,"s",label="岭回归 alpha=1")
plt.plot(ri01.coef_,"^",label="岭回归 alpha=0.1")
plt.plot(ri10.coef_,"v",label="岭回归 alpha=10")
plt.plot(lr.coef_,"o",label="线性回归")
plt.xlabel("系数序号")
plt.ylabel("系数量级")
plt.hlines(0,0,len(lr.coef_))
plt.legend()
可以发现,数据alpha越大,量级越”稳定“,这就是正则化的效果
- 糖尿病实例
from sklearn.linear_model import Ridge
from sklearn.datasets import load_diabetes
diabete = load_diabetes()
x0,x1,y0,y1 = train_test_split(
diabete.data,diabete.target,random_state=0)
ridge = Ridge(alpha=0.1)
ri = ridge.fit(x0,y0)
print("y = ",end=" ")
for w in ri.coef_:
i = 1
print("{:.2f}".format(float(w)) +"[X%s]"%i+" +",end=" ")
i=i+1
print("{:.2f}".format(float(ri.intercept_)))
print(ri.score(x0,y0))
print(ri.score(x1,y1))
结果:
y = -24.58[X1] + -176.86[X1] + 542.07[X1] + 278.68[X1] + -64.30[X1] + -106.36[X1] + -203.48[X1] + 103.46[X1] + 455.48[X1] + 57.87[X1] + 152.86
//并没有一个W是0
0.5502042988482881
0.36901969445308314 //有进步,但还是离我们想要的结果差的远
//有时候你不得不认怂,因为糖尿病问题就是不适合线性模型,选对模型也是很重要的一件事儿
- 葡萄酒实例
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_wine
from sklearn.linear_model import Lasso
wine = load_wine()
x0,x1,y0,y1 = train_test_split(
wine.data,wine.target,random_state=0)
ridge = Ridge(alpha=0.1)
ri = ridge.fit(x0,y0)
print("y = ",end=" ")
for w in ri.coef_:
i = 1
print("{:.2f}".format(float(w)) +"[X%s]"%i+" +",end=" ")
i=i+1
print("{:.2f}".format(float(ri.intercept_)))
print(ri.score(x0,y0))
print(ri.score(x1,y1))
结果:
y = -0.09[X1] + 0.03[X1] + -0.09[X1] + 0.03[X1] + -0.00[X1] + 0.22[X1] + -0.47[X1] + -0.39[X1] + 0.08[X1] + 0.05[X1] + -0.12[X1] + -0.31[X1] + -0.00[X1] + 3.19
0.9185037114126158
0.8062350353487193
- 总结
- 套索回归与回归的对比
如果数据集中有许多特征,但不是每个特征都会对结果产生重要影响,那就用L1
如果数据特征不多,每一个都有重要作用,那就用L2
- 线性回归优点
算法简单,所以快
对于特征数量多的时候,拟合的比较好
>>> import time
>>> time.ctime()
'Wed Sep 11 17:58:28 2019' //博客完成时间