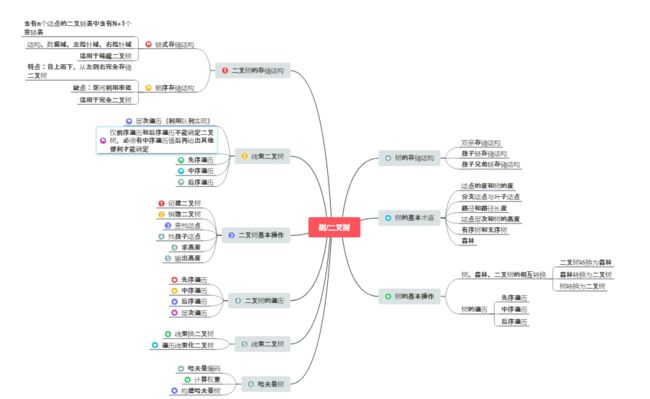
1.思维导图及学习体会
1思维导图
2.谈谈你对树结构的认识及学习体会。
- 1. 树形结构属于非线性结构,常用的树形结构有树和二叉树。树是由n(n>=1)个有限节点组成一个具有层次关系的集合。树的基本术语有:结点的度与树的度;分支节点与叶子结点;路径与路径长度;孩子结点、双亲结点和兄弟结点;结点层次和树的高度等等。树有多种类型,可分为二叉树和哈夫曼树等,其中二叉树又可分为完全二叉树和满二叉树。 在树中主要学习了二叉树和哈夫曼树这种树。
- 2. 二叉树:二叉树是一种特殊的树。二叉树的特点是每个结点最多有两个儿子。二叉树的存储结构可以有顺序存储结构和连式存储结构。可以通过二叉树的疏密以及题目要求等来决定树的存储结构。二叉树遍历的方法有先序遍历、中序遍历、后序遍历与层次遍历四种方法。不论在树的建立或其他基本运算中基本是要运用到递归,代码量少,但是理解起来不容易,而且错误地方不容易调试看出来。
- 3. 树的学习还是学的更懵逼了,特别是一开始递归部分不好理解,而且这章节需要记住的知识点很多,孩子节点、兄弟节点、满二叉树、完全二叉树等等一堆东西,我觉得我脑子已经不够用了,PTA上的题目以及不友好了,特别是表达式还有一堆的编程题,还有需要递归的地方,以及这次大作业,能写出来感觉真是厉害了,这学期真是不容易啊,学的要死要活的...转专业来不及了都
2.PTA实验作业
2.1.题目1:6-4 jmu-ds-表达式树
输入一行中缀表达式,转换一颗二叉表达式树,并求解.
表达式只包含+,-,*,/,(,)运算符,操作数只有一位,且为整数(有兴趣同学可以考虑负数小数,两位数做法)。按照先括号,再乘除,后加减的规则构造二叉树。
如图所示是"1+(2+3)*2-4/5"代数表达式对应二叉树,用对应的二叉树计算表达式的值。 转换二叉树如下:
2.1.1设计思路(伪代码)
void InitExpTree(BTree &T, string str) //建表达式的二叉树
建立字符栈op和树根栈node
创建树结点p等于NULL,a,b
定义i=0表示循环变量 定义字符来存判断两符号的优先关系的函数返回的符号
while 表达式str未结束
if str[i] 是数字字符 then
创建树节点p
将结点存入树栈node中 node.push(p)
else if str[i]是运算符 then
if op.empty() then op.push(str[i]) //如果栈空 则将字符存进去
else
f = Precede(op.top(), str[i]) //判断两符号的优先关系
switch f
case:'>'
从树栈node出栈两个结点存入a,b中
调用CreateExpTree函数创建数二叉树p并入栈
i--
break
case '<':op.push(str[i]); break; //优先级比栈顶元素高
case '=':op.pop(); break;
end while
while 运算符栈op中不为空且栈node也不为空
从树栈node出栈两个结点存入a,b中
调用CreateExpTree函数创建数二叉树p并入栈
end while
double EvaluateExTree(BTree T)
定义浮点数sum,b,m
建立double类型的栈 num表示将每一次计算结果存进去以及取出来
建立字符栈 s表示存入的数据有运算符有数
建立树类型的栈 node表示每次取数的结点
while T
将每个结点的数据一个个存入s,以及将结点T存入node中
end while
while s不为空
if s的栈顶元素为数字 then
将字符转化为数存入num中
else //为运算符时候
sum=num的栈顶元素
num去栈顶元素
b=num的栈顶元素
num去栈顶元素
switch s的栈顶元素
case '+':sum += b; break;
case '-':sum -= b; break;
case '*':sum *= b; break;
case '/':
if b等于0
输出divide 0 error!\n
关闭程序
else sum /= b;
end if
break
s.pop();
num.push(sum);
返回sum2.1.2代码截图
2.1.3本题PTA提交列表说明。
- Q1:一开始提交时候是为多种错误,里面有段错误有答案错误
- A1:当我在判断了栈顶优先级高的时候,搞错了要从node中弹出两个根结点出来,我只弹出一个导致出现错误,主要还是老师给我们讲过了,还给了我们建树的ppt的伪代码,然后才会打...
- Q2:后来只对了五分的情况,是只对了除0错误这个测试点,至于其他两个主要测试点都没过
- A2:这个改了特别久,改了好几天,一直没发现错误,后来发现,原来在建立这棵树的时候,判断符号优先级别时,当Precede返回大于号时候,还要i减一,不然在后面i在加一可能不能一直判断栈顶元素与当前元素的优先级谁高
2.2.题目1:7-4 jmu-ds-二叉树叶子结点带权路径长度和
二叉树叶子结点的带权路径长度指:叶子结点的权重路径长度。本题要求算出二叉树所有叶子结点的带权路径长度和。 如下面的二叉树:
2.2.1设计思路(伪代码)
主要说建树函数和计算权值的函数
BiTree create(string str, int n)
建立新的树节点 BT
if str[n] 等于字符# 返回NULL end if
if n>str.size() - 1 返回NULL end if
BT->data = str[n];
BT->lchild = create(str, 2 * n); //递归建树
BT->rchild= create(str, 2 * n+1);
返回 BT;
void GetWPL(BiTree bt,int h,int&wpl)
if bt等于NULL 返回
end if
if bt左右孩子不空
wpl=wpl+(bt->data-'0')*h;
end if
GetWPL(bt->lchild,h+1,wpl);
GetWPL(bt->rchild,h+1,wpl);
2.2.2代码截图
2.2.3本题PTA提交列表说明。
- Q1:第一次和第二次的只有五分的测试点过了,然后也百度过了也是没出来
- A1:直到正确答案出来我再看一下原来代码,发现错误的是在计算权值的函数中,再对左右子树的搜索中,我是将对左右子树的遍历放在判断是否为叶子结点里面,导致其实没对整颗二叉树进行遍历
- Q2:再第三四次的提交中,还是只有五分,后来上课看了老师的做题后发现了错误
- A2:在传参时候应该先传进去0,而不是传进去1,如果是1的话会导致层数多1,而导致最后结果错误
- Q3:在其中还有就是有时devc有跳错
A3:递归口设置的不对,导致最后到了空时候还进行操作导致出错
***2.3.题目1:7-2 根据后序和中序遍历输出先序遍历
本题要求根据给定的一棵二叉树的后序遍历和中序遍历结果,输出该树的先序遍历结果。
2.3.1设计思路(伪代码)
#include
using namespace std;
int in[31], post[31];
typedef struct BiTNode
{
int data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
BiTree Build(int *in, int *post, int n)//第一个参数是中序序列的起始位置,第二个参数是后序序列的起始位置,n是长度
定义len, *p
if n <= 0 then//如果长度小于等于0,直接返回即可
return NULL
end if
p = in;
for pto in+n //少打了一个+n
if *p == *(post + n - 1) then break
end if
enf for
建立新结点T
T->data = *p
len = p - in;
T->lchild = Build(in, post, len);
T->rchild = Build(p + 1, post + len, n - len - 1);
返回T
void PreOrder(BiTree T)
if T不为空 then
输出 T->data;
PreOrder(T->lchild);
PreOrder(T->rchild);
end if
return
int main()
定义 n, i=0分别表示数组长度和循环变量;
BiTree T;//只需要定义,不需要赋值->[BiTree T = new BiTNode;]
输入 n
for i to n do
输入 post[i]
end for
for i to n do
输入 in[i]
end for
T = Build(in, post, n)
输出"Preorder:"
PreOrder(T)
return 0
2.3.2代码截图
2.3.3本题PTA提交列表说明。
- Q1:多种错误中有答案错误还有格式错误
- A1:格式错误可以解决,那个答案错误,一开始以为应该将p赋值放在循环外,但这个没影响啊,后来是循环条件错了,忘了in是用指针来的,应该p小于in+n
- Q2:再改了循环条件后再次提交就过了一个测试点
- A2:对于形参n,再创建右子树时候错误,本来是写n-len,后来调试一点点画图一点点看时候,发现应该还要再减一才正确
3、阅读代码
3.1 题目 :判断一棵树是否是另一棵树的子树
3.2 解题思路
3.4 学习体会
- 1. 他通过中序和后序来建树和我不太一样,看起来比我方便多了,还多了个形参
- 2.在层次输出那一块的代码,我在打pta的那道题时候,打不出来,然后他用了队列的方法,这个一开始是没想到的,用队列做的确更快,本来我想用递归的