线段树

0 引言

Leetcode307
这道题除了使用树状数组，还可以使用线段树。
线段树是一种平衡二叉树，支持快速区间查找\(O(lgn+k)\)和更新\(O(lgn)\)。

1 线段树

线段树核心思想是叶子结点负责保存原始信息，非叶结点负责其孩子表示范围的union，可以是求和、最值等：

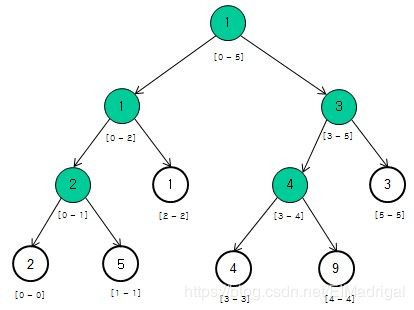
对于每个结点，需要存储起始点、终止点、值、左右指针：

class segTreeNode {
public:
    segTreeNode(int start, int end, int val, segTreeNode* left = nullptr, segTreeNode* right = nullptr) : start(start), end(end), val(val), left(left), right(right) {}

    ~segTreeNode() {
        delete left;
        delete right;
        left = right = nullptr;
    }

    int start;
    int end;
    int val;    // can be sum, min, max...
    segTreeNode* left;
    segTreeNode* right;
};

建树可以通过递归方式进行：

segTreeNode* buildTree(int start, int end, vector& nums) {
    if (start == end)
        return new segTreeNode(start, end, nums[start]);
    int mid = (start + end) / 2;
    auto left = buildTree(start, mid, nums);
    auto right = buildTree(mid + 1, end, nums);
    auto root = new segTreeNode(start, end, left->val + right->val, left, right);
    return root;
}

对于更新操作，只要找到叶子结点，一路向上更新至根结点，复杂度\(O(lgn)\)：

void update(segTreeNode* root, int i, int newVal) {
    if (root->start == i && root->end == i) {
        root->val = newVal;
        return;
    }
    int mid = root->start + (root->end - root->start) / 2;
    if (i <= mid)
        update(root->left, i, newVal);
    else
        update(root->right, i, newVal);
    root->val = root->left->val + root->right->val;
}

对于查询操作，查询范围有三种情况：

1. 范围正好和根结点负责的范围一致，直接返回；
2. 范围由某个下层结点负责，找到该结点返回其值；
3. 范围由两个下层结点组合负责，返回两个结点的sum。

查询最好情况复杂度\(O(1)\)，最坏情况\(O(lgn+k)\)，\(k\)是某层结点的数目：

int query(segTreeNode* root, int i, int j) {
    if (i == root->start && j == root->end)
        return root->val;
    int mid = root->start + (root->end - root->start) / 2;
    if (j <= mid)  // 查询范围完全落在左子树
        return query(root->left, i, j);
    else if (i > mid)  // 查询范围完全落在右子树
        return query(root->right, i, j);
    else
        return query(root->left, i, mid) + query(root->right, mid + 1, j);
}

2 Reference

• 花花酱 Segment Tree 线段树 SP14
• 一步一步理解线段树