NB的程序员,亮瞎了你的眼吗？

郑重声明: 本文首发于人工博客

1、导读

你能想象到1K的代码能写出什么样的功能强大、效果炫酷的作品吗？来吧，今天小编带领大家认识下下面这位大神的作品。

西班牙程序员Roman Cortes用纯JavaScript脚本编写的玫瑰花。
这才是牛逼程序员送给女友的最好情人节礼物呢！(提示：在不同浏览器下观看效果、速度会有很大的不同)

2、先来张效果图

在线预览
预览效果1:

预览效果2

3、原理解读

3.1 蒙特卡罗方法

蒙特卡罗方法是令人难以置信的强大的工具。我用他们所有的时间,对于很多类型的函数优化和抽样问题,他们几乎像魔法一样当你有更多的CPU时间比设计和编码算法。在上升的情况下,它是非常有用的代码大小的优化。
如果你不知道很多关于蒙特卡罗方法,你可以读到他们在这个优秀的维基百科文章。

3.2 明确的表面和采样/绘图

定义的形状玫瑰我使用多个explicit-defined表面。我使用一个共有31表面:24花瓣,萼片4(周围的薄叶花瓣),2叶和1的玫瑰。
这些显式的表面如此,它们是如何工作的?它是很容易的,我要提供一个二维的例子:
首先我定义明确的表面功能:

function surface(a, b) {  // I'm using a and b as parameters ranging from 0 to 1.
    return {
        x: a*50,
        y: b*50
    };
    // this surface will be a square of 50x50 units of size
}

然后,画它的代码:

var canvas = document.body.appendChild(document.createElement("canvas")),
    context = canvas.getContext("2d"),
    a, b, position;

// Now I'm going to sample the surface at .1 intervals for a and b parameters:

for (a = 0; a < 1; a += .1) {
    for (b = 0; b < 1; b += .1) {
        position = surface(a, b);
        context.fillRect(position.x, position.y, 1, 1);
    }
}

结果:

现在,让我们尝试更多密集采样间隔(比间隔=更稠密采样):

正如你所看到的,当你样品越来越密集,点越来越近,到密度时的距离从一个点到他们的邻居比像素更小,表面是完全填充在屏幕上(见0.01)。之后,让它更密集的视觉差异,不会引起太大,你只会画的区域已经(0.01和0.001)的比较结果。
好的,现在让我们重新定义表面函数画一个圆。有多种方法,但是我会使用这个公式:(x-x0) ^ 2 + (y-y0) ^ 2 <半径^ 2,(x0, y0)是圆的中心:

function surface(a, b) {
    var x = a * 100,
        y = b * 100,
        radius = 50,
        x0 = 50,
        y0 = 50;

    if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) {
        // inside the circle
        return {
            x: x,
            y: y
        };
    } else {
        // outside the circle
        return null;
    }
}




if (position = surface(a, b)) {
    context.fillRect(position.x, position.y, 1, 1);
}

结果:

就像我说的,有不同的方法来定义一个圆,他们中的一些人不需要采样的拒绝。我将展示一个方法,但是,正如报告;我不会继续使用它在本文后面:

function surface(a, b) {
    // Circle using polar coordinates
    var angle = a * Math.PI * 2,
        radius = 50,
        x0 = 50,
        y0 = 50;

    return {
        x: Math.cos(angle) * radius * b + x0,
        y: Math.sin(angle) * radius * b + y0
    };
}

(这个方法需要一个密度采样来填补这个比上一个圈)
好,现在让变形圆所以它看起来更像一个花瓣:

function surface(a, b) {
    var x = a * 100,
        y = b * 100,
        radius = 50,
        x0 = 50,
        y0 = 50;

    if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) {
        return {
            x: x,
            y: y * (1 + b) / 2 // deformation
        };
    } else {
        return null;
    }
}

结果:

好,现在这看起来更像玫瑰花瓣的形状。我建议你玩有点变形。你可以使用任何你想要的数学函数,加、减、乘、除,罪恶,因为,战俘…任何东西。只是实验有点修改功能,大量的形状会出现(一些更有趣,更少)。
现在我想添加一些颜色,所以我要将颜色数据添加到表面:

function surface(a, b) {
    var x = a * 100,
        y = b * 100,
        radius = 50,
        x0 = 50,
        y0 = 50;

    if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) {
        return {
            x: x,
            y: y * (1 + b) / 2,
            r: 100 + Math.floor((1 - b) * 155), // this will add a gradient
            g: 50,
            b: 50
        };
    } else {
        return null;
    }
}

for (a = 0; a < 1; a += .01) {
    for (b = 0; b < 1; b += .001) {
        if (point = surface(a, b)) {
            context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";
            context.fillRect(point.x, point.y, 1, 1);
        }
    }
}

结果:

3.3 3D曲面和透视投影

定义3d曲面很简单:只需向surface函数添加一个z属性

function surface(a, b) {
    var angle = a * Math.PI * 2,
        radius = 100,
        length = 400;

    return {
        x: Math.cos(angle) * radius,
        y: Math.sin(angle) * radius,
        z: b * length - length / 2, // by subtracting length/2 I have centered the tube at (0, 0, 0)
        r: 0,
        g: Math.floor(b * 255),
        b: 0
    };
}

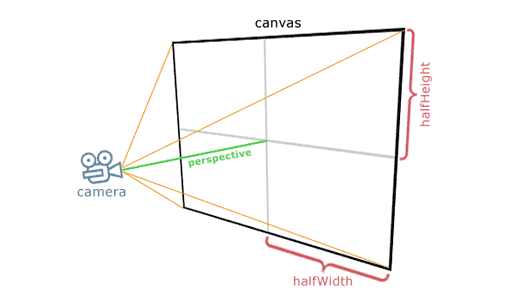
现在，添加透视投影，首先我们必须定义一个相机:

结果:

我将我的相机放在(0,0,cameraZ)，我将调用“透视图”的距离，从相机到画布。我将考虑我的画布在x/y平面上，以(0,0,cameraZ + perspective)为中心。现在，每个采样点将被投影到画布:

var pX, pY,  // projected on canvas x and y coordinates
    perspective = 350,
    halfHeight = canvas.height / 2,
    halfWidth = canvas.width / 2,
    cameraZ = -700;

for (a = 0; a < 1; a += .001) {
    for (b = 0; b < 1; b += .01) {
        if (point = surface(a, b)) {
            pX = (point.x * perspective) / (point.z - cameraZ) + halfWidth;
            pY = (point.y * perspective) / (point.z - cameraZ) + halfHeight;
            context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";
            context.fillRect(pX, pY, 1, 1);
        }
    }
}

结果如下：

3.4 Z-buffer

z-buffer是计算机图形学中很常见的一种技术，它可以在距离摄像机较近的点上绘制距离摄像机较远的点。它的工作原理是保持一个数组与每像素画近z的图像。

这是可视化的z缓冲的玫瑰，与黑色的相机远，白色接近它。
实现:

var zBuffer = [],
    zBufferIndex;

for (a = 0; a < 1; a += .001) {
    for (b = 0; b < 1; b += .01) {
        if (point = surface(a, b)) {
            pX = Math.floor((point.x * perspective) / (point.z - cameraZ) + halfWidth);
            pY = Math.floor((point.y * perspective) / (point.z - cameraZ) + halfHeight);
            zBufferIndex = pY * canvas.width + pX;
            if ((typeof zBuffer[zBufferIndex] === "undefined") || (point.z < zBuffer[zBufferIndex])) {
                zBuffer[zBufferIndex] = point.z;
                context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";
                context.fillRect(pX, pY, 1, 1);
            }
        }
    }
}

3.5旋转这个圆柱体

你可以使用任何向量旋转方法。对于玫瑰，我使用了欧拉旋转。让我们实现一个绕Y轴的旋转:

function surface(a, b) {
    var angle = a * Math.PI * 2,
        radius = 100,
        length = 400,
        x = Math.cos(angle) * radius,
        y = Math.sin(angle) * radius,
        z = b * length - length / 2,
        yAxisRotationAngle = -.4, // in radians!
        rotatedX = x * Math.cos(yAxisRotationAngle) + z * Math.sin(yAxisRotationAngle),
        rotatedZ = x * -Math.sin(yAxisRotationAngle) + z * Math.cos(yAxisRotationAngle);

    return {
        x: rotatedX,
        y: y,
        z: rotatedZ,
        r: 0,
        g: Math.floor(b * 255),
        b: 0
    };
}

3.6 蒙特卡洛取样

我在文章中使用了基于时间间隔的抽样。它需要为每个表面设置一个适当的间隔。如果间隔很大，渲染速度会很快，但最终会在表面留下一些没有填充的洞。另一方面，如果间隔太短，则呈现增量的时间会达到无法接受的数量。
那么，让我们切换到蒙特卡罗抽样:

var i;

window.setInterval(function () {
    for (i = 0; i < 10000; i++) {
        if (point = surface(Math.random(), Math.random())) {
            pX = Math.floor((point.x * perspective) / (point.z - cameraZ) + halfWidth);
            pY = Math.floor((point.y * perspective) / (point.z - cameraZ) + halfHeight);
            zBufferIndex = pY * canvas.width + pX;
            if ((typeof zBuffer[zBufferIndex] === "undefined") || (point.z < zBuffer[zBufferIndex])) {
                zBuffer[zBufferIndex] = point.z;
                context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";
                context.fillRect(pX, pY, 1, 1);
            }
        }
    }
}, 0);

现在，a和b参数被设置为两个随机值。采样足够的点，表面就会以这种方式完全填充。我每次画10000个点然后让屏幕根据间隔更新。

另外，只有在伪随机数发生器质量良好的情况下，才能保证曲面的完全填充。在一些浏览器中，数学。随机是用一个线性同余发生器实现的，这可能会导致一些曲面的问题。如果你需要一个好的PRNG采样，你可以使用高质量的像Mersenne Twister(它有JS实现)，或者在一些浏览器中可用的加密随机生成器。使用低差异序列也是非常明智的。

4、总结

完成玫瑰，玫瑰的每一部分，每一个表面，都是同时呈现的。我为函数添加了第三个参数，该函数选择玫瑰的部分来返回一个点。数学上它是一个分段函数，每一块都代表玫瑰的一部分。在花瓣的例子中，我使用旋转和拉伸/变形来创建所有的花瓣。所有的工作都是通过混合本文中暴露的概念来完成的。

虽然通过采样显式表面是一种非常著名的方法，也是最古老的3d图形方法之一，但我的分段/蒙特卡罗/z-buffer方法可能很少像我这样用于艺术目的。虽然不是非常具有创新性，在实际场景中也不是很有用，但是它非常适合js1k的环境，在这种环境中，简单性和最小的大小都是需要的。

通过这篇文章，我真的希望能够激励那些对计算机图形感兴趣的读者去尝试和享受不同的渲染方法。在图形领域有一个完整的世界，研究和使用它是令人惊奇的。

---

版权声明：本文为人工博客的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
本文链接：https://www.94rg.com/article/1724