红黑树又称二叉搜索树,它主要是通过红和黑两种颜色(red、black)来标识节点。通过对任何一条从根节点到叶子节点路径上的节点颜色进行约束,红黑树保证最长路径不超过最短路径的两倍,所以说:红黑树是近似于平衡的。
■下面是红黑树的主要特点:
(1)红黑树的根节点是黑色的。
(2)红黑树中若一个节点是红色的,则它的两个子节点必须是黑色的。
(3)红黑树中从该节点到后代叶节点的路径上,黑色节点数目是相同的。
◆红黑树的应用:
C++库、linux内核、java库等
◆红黑树与AVL树的区别:
红黑树和AVL树都是高效的平衡搜索树,时间复杂度都是O(lgN);
红黑树对平衡的要求不是特别高,它只需要满足最长路径不超过最短路径的两倍,所以性能相对较高。
■下面是红黑树中节点结构:
enum color //枚举节点的两种颜色
{
RED,
BLACK,
};
template
struct RBTreeNode
{
color _col;
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;
K _key;
V _value;
RBTreeNode(const K& key, const V& value)
:_key(key)
, _value(value)
, _left(NULL)
, _right(NULL)
, _parent(NULL)
, _col(RED) //颜色必须插入的是红色,因为要保证黑色节点的个数是平衡的
{ }
};
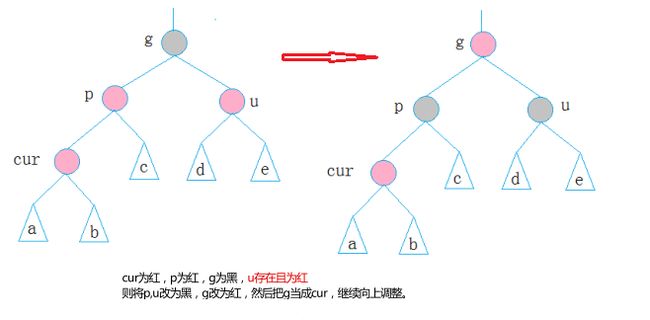
■下面分析红黑树的插入情况:
(1)
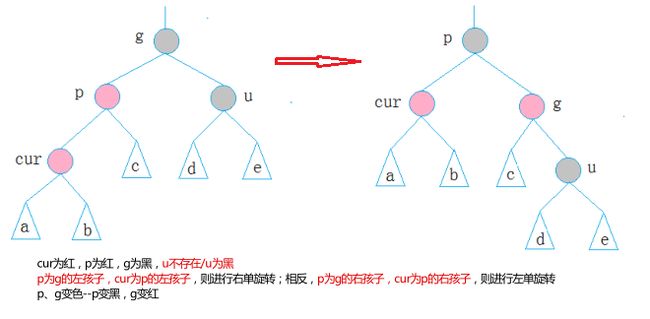
(2)
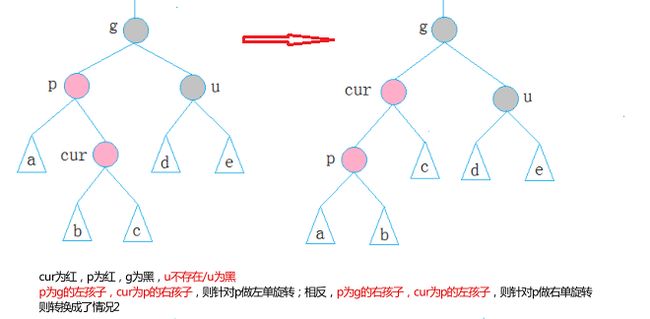
(3)
■下面是主要的代码:
#pragma once
//实现红黑树的基本功能
/*
1.红黑树中的节点只能是红色或者黑色
2.红黑树的根节点为黑色
3.红黑树的左、右子树的黑色节点个数是相同的
4.红黑树中红色节点的两个孩子节点必须都为黑色节点
*/
enum color //枚举节点的两种颜色
{
RED,
BLACK,
};
template
struct RBTreeNode
{
color _col;
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;
K _key;
V _value;
RBTreeNode(const K& key, const V& value)
:_key(key)
, _value(value)
, _left(NULL)
, _right(NULL)
, _parent(NULL)
, _col(RED) //颜色必须插入的是红色,因为要保证黑色节点的个数是平衡的
{ }
};
template
class RBTree
{
typedef RBTreeNode Node;
public:
RBTree()
:_root(NULL)
{}
bool Insert(const K& key, const V& value)
{
if (_root == NULL) //根节点为空的情况,必须将根节点置为黑色
{
_root = new Node(key, value);
_root->_col = BLACK;
return true;
}
Node* cur = _root;
Node* parent = NULL;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
break;
}
}
//寻找到数据该插入的位置
if (parent->_key < key)
{
Node* tmp = new Node(key, value);
parent->_right = tmp;
tmp->_parent = parent;
}
else if (parent->_key > key)
{
Node* tmp = new Node(key, value);
parent->_left = tmp;
tmp->_parent = parent;
}
//处理(如果父节点为黑色,则不用对树进行调整,树保持红黑树的状态)
while(cur != _root && parent->_col == RED)
//插入的不是根节点,且父节点的颜色为红
{
Node* grandFather = parent->_parent;
if (parent == grandFather->_left)
{
Node* uncle = grandFather->_right;
//情况一:需要将祖父节点置为红色,将父亲节点和叔叔节点置为黑色,
//下次直接从祖父节点向上进行调整
if (uncle != NULL && uncle->_col == RED)
{
grandFather->_col = RED;
parent->_col = BLACK;
uncle->_col = BLACK;
cur = grandFather;
parent = cur->_parent;
}
else
{
//情况二:需要先进行右单旋,然后将父亲节点置为黑色,祖父节点置为红色
//情况三:需要先进行左单旋,然后就会转化为情况二
if (cur == parent->_right && parent->_right != NULL) //情况三左、右
{
_RotateL(parent);
}
parent->_col = BLACK;
grandFather->_col = RED;
_RotateR(grandFather);
}
}
else //父亲节点为祖父节点的右节点
{
Node* uncle = grandFather->_left;
//情况一:需要将祖父节点置为红色,将父亲节点和叔叔节点置为黑色,
//下次直接从祖父节点向上进行调整
if (uncle != NULL && uncle->_col == RED)
{
grandFather->_col = RED;
parent->_col = BLACK;
uncle->_col = BLACK;
cur = grandFather;
parent = cur->_parent;
}
else
{
//情况二:需要先进行左单旋,然后将父亲节点置为黑色,祖父节点置为红色
//情况三:需要进行右单旋,然后就会转化为情况二
if (cur == parent->_left && parent->_left != NULL)//情况三右、左
{
_RotateR(parent);
}
parent->_col = BLACK;
grandFather->_col = RED;
_RotateL(grandFather);
}
}
}
_root->_col = BLACK;
return true;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool Check() //检查是否为红黑树
{
int countBlack = 0;
Node* cur = _root;
while (cur->_left != NULL) //统计一条路径上的黑色节点的数目
{
if (cur->_col == BLACK)
{
countBlack++;
}
cur = cur->_left;
}
return _Check(_root, 0, countBlack);
}
protected:
bool _Check(Node* root, int blackNum, int curBalanceNum)
{
if (root == NULL)
{
return false;
}
if (root->_parent != NULL && root->_col == BLACK)
{
if (root->_parent->_col == RED)
{
return true;
}
}
if (root->_left == NULL && root->_right == NULL) //递归到叶子节点是的黑色节点数目是否相等
{
if (blackNum == curBalanceNum)
{
return true;
}
else
{
return false;
}
}
return _Check(root->_left, blackNum++, curBalanceNum)
&& _Check(root->_right, blackNum++, curBalanceNum);
}
void _InOrder(Node* root)
{
if (root == NULL)
{
return;
}
_InOrder(root->_left);
cout << root->_key <<":"<_col<_right);
}
void _RotateL(Node*& parent) //左单旋
{
Node* SubR = parent->_right; //新建两个节点指针
Node* SubRL = SubR->_left;
parent->_right = SubRL; //进行调整
if (SubRL)
{
SubRL->_parent = parent;
}
SubR->_left = parent;
SubR->_parent = parent->_parent;
parent->_parent = SubR;
parent = SubR;
if (parent->_parent == NULL) //parent为根节点的情况
{
_root = parent;
}
else //parent不为根节点
{
Node* ppNode = parent->_parent;
if (ppNode->_key > parent->_key)
{
ppNode->_left = parent;
}
else
{
ppNode->_right = parent;
}
}
}
void _RotateR(Node*& parent) //右单旋
{
Node* SubL = parent->_left; //新建两个节点指针
Node* SubLR = SubL->_right;
parent->_left = SubLR; //进行调整
if (SubLR)
{
SubLR->_parent = parent;
}
SubL->_right = parent;
SubL->_parent = parent->_parent;
parent->_parent = SubL;
parent = SubL;
if (parent->_parent == NULL) //parent为根节点的情况
{
_root = parent;
}
else //parent不为根节点
{
Node* ppNode = parent->_parent;
if (ppNode->_key > parent->_key)
{
ppNode->_left = parent;
}
else
{
ppNode->_right = parent;
}
}
}
protected:
Node* _root;
};
void Test()
{
RBTree ht;
ht.Insert(5, 1);
ht.Insert(9, 1);
ht.Insert(3, 1);
ht.Insert(1, 1);
ht.Insert(8, 1);
ht.Insert(2, 1);
ht.Insert(4, 1);
ht.Insert(6, 1);
ht.Insert(7, 1);
ht.InOrder();
cout<