卡尔曼滤波剪影__Kalman Filtering

<本文采用CC-BY-NC-SA 4.0 Int'l协议，共享时请署名并注明采用相同的协议，不用于任何商业用途。>

铺垫用の引论

Kalman Filtering 算法是一种最优滤波估计算法，有了它之后，就算只知道观测对象的少量不准确观测信息也有可能对这一对象实现完全控制，它的Advantages和Disadvantages(Constraints)在下面分别以标黑"匚"以及普通"匚"记录下来。

(DIS)Advantages总览

Can be operated on a continuous function or a discrete function;
Can handle not only stationary processes, but also non-stationary and multidimensional processes;
Faster speed;
Well suited for embedded systems, and real time problems;
Smaller memory requirements;
When information about the initial state is unknown and no prior knowledge is available, KF can be extended to EKF, thus solve the problem;
It is expected to be mixed with artificial neural networks, to gain some newer properties;
The object must be in the time domain, and the discrete model can be constructed;
The runtime is limited by the computer hardware, which leads to the singularity of the covariance matrix in the process of calculation transfer, so there will be great instability in the numerical calculation, these can be avoided by its extension such as Singular Value Filter, UD Decomposition Filter, Particle Filter;
Ordinary filtering must be recursive and applied to linear systems, while non-linearity needs to be replaced by EKF with high complexity. Recursion is also not conducive to stack management in C++.

利用分而治之的思想，可以分两步理解这个算法：

"Filtering"的理解

这个词由Telecommunication的信号处理工程引入，在信息传输过程中，噪声使信息很难从信源准确无误地到达信宿因此，怎样除去噪声的影响^[1]，从所获得的信息(含有噪声等干扰因素故不准确)中提取出人们想要的那一部分就成了一个重要的课题，就是专门用来解决这一问题的操作。这种除掉噪声的目的，可以通过

1.时域中进行某些奇异的运算提取出想要的信息;

频域中将处于某些频段信息分量提取出来;

两种方法实现，它们都可以反过来看做是将观测得到的数据处理后得到相应参数的估计值，被叫做“滤波估计”，第二类滤波方法在早期滤波估计中较为常见，它们大多是基于Fourier变换的一些应用方法并且在信号处理领域大显身手，其中，于1940被提出的Wiener滤波作为一种基于频域的统计最优滤波器，开启了对于随机信号进行处理的先河，然而它因为频域的限制，只能处理一维平稳随机信号。而第一类滤波方法是近代才兴起的，它们有更加广泛的应用范围以及更优良的性能，即如何从已知的(不精确)数据中估计出准确信息，具有代表性且最为常用的就是Kalman Filtering算法。

综上，可以将滤波这件事总结为：

`滤波的实质, Vernacularism`

为最大限度上降低信息在传输过程中收到的噪声干扰，对于所接收到的各种随机信号的混合信号进行处理，并得到此条件下最优估计信号的方法，就是滤波.

"KF"的应用

但话说回来，Kalman Filtering^[2]一经发明，就成为了应用范围最广泛的滤波算法，其最早的工程应用是在Apollo moon landing program，在这个登月项目中，需要通过温度传感器测得的火箭燃料温度进行动力控制，然而火箭燃料温度超高，一般的温度传感器在里面根本不能生存，这时Kalman Filtering就派上用场了，温度传感器可以用来间接地测量火箭外围的温度，根据观测到的这一数据，Kalman Filtering就能预测到真实的燃料温度，如下图所示。

卡尔曼滤波剪影__Kalman Filtering · Make Intuitive_第1张图片

Rocket_Draft.jpg

想要切实地解决掉一个最优估计问题，需要的大多不仅仅是所测量得到的数据们，也需要如下这些部分(可以看作是最优估计问题的组分)：<1>先验知识，即已知的一些问题相关的物理量；<2>约束条件，即问题中某些参数或系统必须满足的条件；<3>估计准则函数，用来评判一个估计解决方案的优劣。领会Kalman Filtering就是在学习求解最优估计问题，有必要形成一个遇到问题后将<1><2><3>分别对号入座的意识。

下面列举出来了这种滤波算法超广泛的应用场景，可以见到，它几乎覆盖了所有与信息处理有些许关联的领域... ...会Kalman Filtering的人理论上真就能解决所有的观测信号真实信号的转换问题。

通信

定位、跟踪

图像处理领域

卫星导航等速度方向的估计

语音信息重建领域

地质勘探，有效整合各种传感器送来的信息

天气、地震预报

证券和股票行情预测

医疗行业，这种估计方式能参与诊断某些具有统计特征的病症

Kalman Filteringの详述

根据上述铺垫，KF在这里所解决的问题是：求解一种Operation它以"随机信号的观测值"作为输入，以"信息处理后得到的估计参数/研究对象当前的状态"作为输出。，为清楚起见，可以用下图来表示Kalman Filtering所充当的角色，就算不了解算法的真正原理，你也可以把它当作一个黑匣子无脑使用。

Apollo_machine.png

可以看到，原则上来说，我们往Kalman Filter这个滤波机器内投入每一个观测时刻的观测值，它就能以你投入观测值的频率不断吐出你想要的对应时刻的系统参数或者对象状态了。接下来就要具体看一看这个算法到底是怎样一回事了。

`Assumption, 事前設定`

要想用KF来解决之前说的最优估计问题，此问题需要满足以下预设条件：^[3]-[5]

1.系统状态的变量是随机变量，且满足Gaussian Distribution

系统可能受到的外界影响是满足叠加定律且已知的

测量噪声存在，且为高斯白噪声

只适用于线性系统，非线性则采用Extended Kalman Filtering

`Modeling Formulation, 実体、正規化`

首先，对于研究对象进行建模，观测系统在第个时间段所在的状态，可以由一个状态向量来描述，例如说一个车站就是研究对象，那它的状态向量可能就是下面这个样子：
$\color{deeppink}{\mathbf{\hat{x}}_{k}} \color{black}{= \begin{bmatrix} 車両台数\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Num\\ 車両の流れ\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Phi_{Car}\\ \vdots\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \end{bmatrix}}$
更详细一些的话，一个对象的状态向量是一个包裹，里面装了你想在时刻了解到的属于对象的所有有关信息(精确的)，例如时的车辆数++++++++，车流量。为什么要用而不是呢？这是因为在观测前，对象当前的状态对于我们而言是含糊不清的，一般只能知道好多近似信息，因此，我们使用随机分布来表示对象的状态，根据假设1.，它们满足Gaussian Distribution。^[6]

依据时刻的状态向量，根据牛顿决定论，我们原则上能够预测出时刻的状态向量，因此，可以引入一个线性变换矩阵(一说，预测矩阵Prediction Matrix)，这样可以由前一时段的状态向量表示为

如果进一步考虑到外界对于系统的控制，则控制部分也应计入我们预测的状态向量中去，根据假设2.，我们已经知道了控制矩阵以及控制向量，可以将这一影响叠加在前述的基础上，因此有
$\begin{equation} \begin{split} \color{deeppink}{\mathbf{\hat{x}}_k} \color{black}{= \mathbf{F}_k} \color{royalblue}{\mathbf{\hat{x}}_{k-1}} \color{black}{+} \mathbf{B}_k \color{darkorange}{\vec{\mathbf{u}_k}} \end{split} \end{equation}$
另一方面，为了充分挖掘出状态向量带给我们的信息，从而更好地完成估计的任务，我们也应将状态向量中个元素之间的关系考虑在内，每两个元素(随机变量)之间的关系可以由叫做“协方差”的量来描述^[6]，它定义为，即两个随机变量同时减去各自均值的期望，所有协方差按照的顺序排列所得的矩阵成为协方差矩阵，容易看出，每一个状态向量就对应着一个协方差矩阵，根据，可以得到时刻与时刻的协方差矩阵之间的关系

如果进一步考虑来自环境的额外的干扰，在预测/估计的时候就可以在所得的协方差矩阵中加入一个不确定性作为修正，这里并不需要考虑这一额外因素对于状态向量本身的影响，因为不确定性仅带来随机变量方差的变化，而不会对其均值产生影响，因此，我们预测出的协方差矩阵应为

另外，传感器对于研究对象的观测被认为是一个线性系统模型，它在时刻给出的状态向量和协方差矩阵为
$\begin{equation} \begin{split} \vec{x}_{expected}\color{black}{}&= \color{fuchsia}{\mathbf{H}_k} \color{deeppink}{\mathbf{\hat{x}}_{k}}\\ \Sigma_{expected} = P_{expected}&=\color{fuchsia}{\mathbf{H_k}} \color{deeppink}{\mathbf{P}_{k}} \color{fuchsia}{\mathbf{H}_k^T} \end{split} \end{equation}$
上式就是只凭借预测得到的最终答案，然而，我们还未利用实际测量得到的值：一个是测量得到的观测值(均值)，另一个是观测值向量的协方差矩阵。Kalman Filtering的工作就是怎么权衡好这两个组所得的值，最终给出一个最优的估计结果。

综上，正规化的字母描述如下表所示(包含的未出现字母会在Processing中给出诠释)：

Variables (Described)	Symbols (in LaTeX)
时刻，研究对象的状态向量
研究对象在时刻预测部分的协方差
时刻，研究系统的状态向量
研究对象在时刻统计分布的协方差
时刻的控制矩阵
时刻的控制向量
目标为时刻状态向量，我们的预测矩阵
目标为时刻状态向量，传感器的观测矩阵
时刻来自外界的额外不确定性
时刻传感器观测值的值(即观测值的均值)
时刻传感器观测值的协方差
Kalman系数，时刻以及时刻的值
时刻，状态向量的最优估计
时刻，最优估计状态向量的协方差

`Processing, 具象処理`

下面是！很重要的一个环节！为了使ni更加深刻地理解KF的算法套路，这里我们慢一些行进。

Kalman Filtering的思维分为五个步骤，它大体遵循着自回归算法的策略，利用对于状态和协方差的预测数据(时间更新，上文已给出)来更新二者的值(预测更新)，而后又返回来根据新的状态和协方差来更改预测数据... ...

根据前述，剩下的步骤就是怎样有效地将以及融合在一起，它们是两个概率分布，且都服从Gaussian Distribution，将它们画在一张图中，如下图所示，可以推测，最优的估计值大概率会出现在二者的交集处。

卡尔曼滤波剪影__Kalman Filtering · Make Intuitive_第2张图片

Fig_for_multiply_Gaussian.jpg

由此可知，从两个Gaussian Distribution中取得最优估计的过程就是求二者乘积的过程。

两个一维Gaussian Distribution的乘积会是个什么样的分布呢？答案是：仍然是一个Gaussian Distribution，它的均值和方差(注意这里，一维概率分布中的方差就是它的协方差)为
$\begin{equation} \begin{aligned} \color{royalblue}{\mu’} &= \mu_a + \frac{\sigma_a^2 (\mu_b – \mu_a)} {\sigma_a^2 + \sigma_b^2}\\ \color{mediumblue}{\sigma’}^2 &= \sigma_a^2 – \frac{\sigma_a^4} {\sigma_a^2 + \sigma_b^2} \end{aligned} \end{equation}$
这样的公式或许缺少了一些直观性，可以引入系数，这样，上式可记作：
$\begin{equation} \begin{split} \color{royalblue}{\mu’} &= \mu_a + &\color{purple}{\mathbf{k}} (\mu_b – \mu_a)\\ \color{mediumblue}{\sigma’}^2 &= \sigma_a^2 – &\color{purple}{\mathbf{k}} \sigma_a^2 \end{split} \label{update} \end{equation}$
可以看到，新的概率分布系数，都是由原来的分布系数加上同一个系数乘上一个“修正值”得到的！将这一思想推广至高维统计分布，也应如此，即：更新后的最优融合估计值可以描述为根据前一时刻得出的估计值加上这一时刻传感器给出的修正：
$\begin{equation} \begin{split} \color{royalblue}{\vec{\mu}’} &= \vec{\mu_a} + &\color{purple}{\mathbf{K}} (\vec{\mu_b} – \vec{\mu_a})\\ \color{mediumblue}{\Sigma’} &= \Sigma_a – &\color{purple}{\mathbf{K}} \Sigma_a \end{split} \label{matrixupdate} \end{equation}$
其中的被称作Kalman系数，表示为

由前述分析可知，有
$\begin{equation} \begin{split} \begin{array}{} \Sigma_a &= \ \ \color{fuchsia}{\mathbf{H_k}} \color{deeppink}{\mathbf{P}_{k}} \color{fuchsia}{\mathbf{H}_k^T} \\ \Sigma_b &= \ \ \color{mediumaquamarine}{\mathbf{R}_k} \\ \mu_a &= \ \ \color{fuchsia}{\mathbf{H}_k} \color{deeppink}{\mathbf{\hat{x}}_{k}} \\ \mu_b &= \ \ \color{yellowgreen}{\vec{\mathbf{z}_k}} \end{array} \end{split} \end{equation}$
代入(9)，(10)式，得到用于Updation的式子如下
$\begin{equation} \begin{split} \color{fuchsia}{\mathbf{H}_k}\color{royalblue}{\mathbf{\hat{x}}_k’} &= \color{fuchsia}{\mathbf{H}_k}\color{deeppink}{\mathbf{\hat{x}}_k} & + & \color{purple}{\mathbf{K}} ( \color{yellowgreen}{\vec{\mathbf{z}_k}} \color{black}{-} \color{fuchsia}{\mathbf{H}_k}\color{deeppink}{\mathbf{\hat{x}}_k} \color{black}{)} \\ \color{fuchsia}{\mathbf{H}_k}\color{royalblue}{\mathbf{P}_k’} &= \color{fuchsia}{\mathbf{H}_k}\color{deeppink}{\mathbf{P}_k} & – & \color{purple}{\mathbf{K}} \color{fuchsia}{\mathbf{H}_k} \color{deeppink}{\mathbf{P}_k} \end{split} \end{equation}$
Kalman系数为
$\color{purple}{\mathbf{K}} = \color{fuchsia}{\mathbf{H}_k}\color{deeppink}{\mathbf{P}_k}\color{fuchsia}{ \mathbf{H}_k^T} ( \color{fuchsia}{\mathbf{H}_k \color{deeppink}{\mathbf{P}_k} \color{fuchsia}{\mathbf{H}_k^T}} \color{black}{+} \color{mediumaquamarine}{\mathbf{R}_k}\color{black}{)^{-1}}$
此时为计算方便，可以将从三个式子中同时除去，用代替原来的Kalman系数，最终的结果作为Updation步骤与前一部分(Prediction步骤，(3)，(5))一同在下面的全流程中以(15), (16)出现... ...

Kalman Filtering Algorithm:

Prediction:

$\begin{equation} \begin{split} \color{deeppink}{\mathbf{\hat{x}}_k} &= \color{black}{\mathbf{F}_k} \color{royalblue}{\mathbf{\hat{x}}_{k-1}}\color{black}{ + \mathbf{B}_k }\color{darkorange}{\vec{\mathbf{u}_k}} \\ \color{deeppink}{\mathbf{P}_k} &= \color{black}{\mathbf{F}_k} \color{royalblue}{\mathbf{P}_{k-1}} \color{black}{\mathbf{F}_k^T +} \color{mediumaquamarine}{\mathbf{Q}_k} \end{split} \label{kalpredictfull} \end{equation}$

Updation:

$\begin{equation} \begin{split} \color{royalblue}{\mathbf{\hat{x}}_k’} &= \color{deeppink}{\mathbf{\hat{x}}_k} & + & \color{purple}{\mathbf{K'}} ( \color{yellowgreen}{\vec{\mathbf{z}_k}} \color{black}{-} \color{fuchsia}{\mathbf{H}_k}\color{deeppink}{\mathbf{\hat{x}}_k} \color{black}{)} \\ \color{royalblue}{\mathbf{P}_k’} &= \color{deeppink}{\mathbf{P}_k} & – & \color{purple}{\mathbf{K'}} \color{fuchsia}{\mathbf{H}_k} \color{deeppink}{\mathbf{P}_k} \end{split} \end{equation}$

$\color{purple}{\mathbf{K'}} = \color{deeppink}{\mathbf{P}_k}\color{fuchsia}{ \mathbf{H}_k^T} ( \color{fuchsia}{\mathbf{H}_k \color{deeppink}{\mathbf{P}_k} \color{fuchsia}{\mathbf{H}_k^T}} \color{black}{+} \color{mediumaquamarine}{\mathbf{R}_k}\color{black}{)^{-1}}$

这种递归过程最终是否能收敛到一个最优解是由给定的参数初值决定的，因此给定初值也算是一项重要环节。

综上所述，可以将Kalman Filtering的算法流程用以下流程图概括为^[7]

卡尔曼滤波剪影__Kalman Filtering · Make Intuitive_第3张图片

Oil_Chart_for_KF.png

`Final EKF, 開拓`

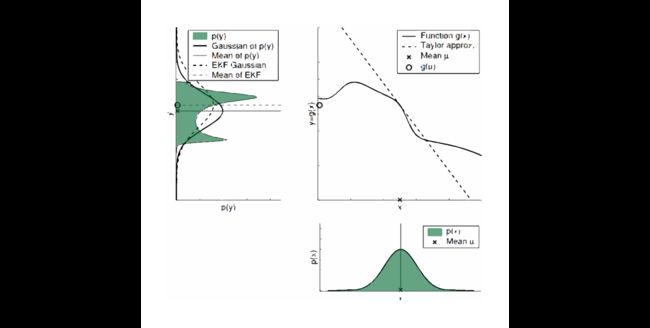
前面讨论的算法(KF)仅适用于线性系统，然而对于非线性系统而言，输入一个满足Gaussian Distribution的变量，其输出并非Gaussian Distribution，举个栗子，下图证明了这一点，这里是用以描述系统的非线性函数，将满足Gaussian Distribution的变量输入，其输出会变成一个奇奇怪怪的家伙(见下图左侧)^[8]。

卡尔曼滤波剪影__Kalman Filtering · Make Intuitive_第4张图片

Oil_Graph_of_EKF.png

非线性系统里，我们一开始使用的方程中，我们的预测以及传感器的观测都演化为以下非线性向量函数
$\begin{equation} \begin{split} \color{deeppink}{\mathbf{\hat{x}}_k} \color{black}{}&= g(\color{royalblue}{\mathbf{\hat{x}}_{k-1}}\color{black}{,}\color{darkorange}{\vec{\mathbf{u}_k}}\color{black}{)}\\ \vec{x}_{expected} &= h(\color{deeppink}{\mathbf{\hat{x}_k}}\color{black}{}) \end{split} \end{equation}$
其中，是非线性连续函数，为应对这类情形，扩展卡尔曼滤波(Extended Kalman Filtering, EKF)被发明出来，专门用来处理非线性系统的滤波问题，我们用下面的伪代码将KF-EKF进行对比，从而给出更加直观的解释：

卡尔曼滤波剪影__Kalman Filtering · Make Intuitive_第5张图片

KF-EKF.png

可见，除了(17)式中所提到的变化外，KF中的都被所替代，都被所替代，它们分别为两个非线性函数的线性近似(即矩阵求导的Jacobi矩阵)：
$\begin{equation} \begin{split} \mathbb{F}_k &= \frac{\partial g(\hat{x}_{k-1},\hat{u}_k)}{\partial \hat{x}_{k-1}}\\ \mathbb{H}_k &= \frac{\partial h(\hat{x}_{k})}{\partial \hat{x}_{k}} = \begin{bmatrix} \frac{\partial h(\hat{x}_1)}{\partial \hat{x}_1}&\frac{\partial h(\hat{x}_1)}{\partial \hat{x}_2}&\cdots&\frac{\partial h(\hat{x}_1)}{\partial \hat{x}_n}\\ \frac{\partial h(\hat{x}_2)}{\partial \hat{x}_1}&\frac{\partial h(\hat{x}_2)}{\partial \hat{x}_2}&\cdots&\frac{\partial h(\hat{x}_2)}{\partial \hat{x}_n}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial h(\hat{x}_n)}{\partial \hat{x}_1} & \frac{\partial h(\hat{x}_n)}{\partial \hat{x}_2} & \cdots & \frac{\partial h(\hat{x}_n)}{\partial \hat{x}_n} \end{bmatrix} \end{split} \end{equation}$
综上，我们已经覆盖了关于KF以及EKF的所有基础内容，可以知道实际上EKF只是将非线性函数线性化后套用KF的框架而已，由于需要求解Jacobian极大增加了算法的复杂度，EKF在实际生活中的应用要远少于KF。

Codebaseの整备场

(∪.∪ )...zzz，下面是一个实例，为更好地证实KF算法在实际Coding中的简易性以及具体操作流程给出了相应的佐证，框架是利用C++编写，借助于MATLAB进行了最终的二次处理，实现了试验结果的可视化。

//The source code are prepared in the supplement files
See../"Kalman_fi.h", ../"Kalman_fi.cpp", ../"Kalman_fi.mlx"

但是你会逐渐发现算法本身以及代码实现并不是影响大家学习Kalman Filtering的原因，关键在于理解它和套用它，并不是所有的领域内都有像火箭燃料那样子有个间接观测量，这时就需要自己去寻找适合的观测量去与想要估计的参数之间的关系，这种先验是很重要的。无论如何，我们还是来落到实处，具体地体会一下Kalman Filtering在实际问题中提供的具体方案。

案例，AHSの无偏估计

作为一个真实的，能够很好地帮助理解的栗子，希望滤除噪声，使得航向姿态系统^[8]中的陀螺仪尽量精确地反映出所观测物理量的真实值，Kalman Filtering 在这里作为一种首选的方法，能很好地适应线性系统的估值，然而对于这里的非线性系统(是一个含有多个角度值的模型，由四元数表征)，却只能提供EKF这种暴力、不利于计算机高效实现的方法(见上文，需要求一个Jacobi矩阵)，由此，在工程中利用Hamilton算子改写状态方程为线性形式，使KF算法能够直接应用于问题中是一个很好的策略。

此案例取自^[10]-[14]。

`ref-用上的和further reading`

[1] 这里指广义噪声，即混在信息中的一些干扰因素，如你喜欢的xka和你表白时，第三方在一旁大声说话/打闹

[2] Kalman R E. A new approach to linear filtering and prediction problems[J]. Journal of basic Engineering, 1960, 82(1): 35-45.

[3] https://www.cnblogs.com/TIANHUAHUA/p/8473029.html

[4] http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/#mathybits

[5] http://home.wlu.edu/~levys/kalman_tutorial/

[6] 这里给出一个示意图，满足高斯分布的变量会像下图一样，有均值和方差

卡尔曼滤波剪影__Kalman Filtering · Make Intuitive_第6张图片

Gaussian_Distribution.png

协方差代表两个随机变量之间的正比例、反比例或“无”的关系，下面的图示给出了协方差大于、小于、等于零时的二维分布图像，它们分别对应着两个变量呈成比例关系，反比例关系，无显性关系。

卡尔曼滤波剪影__Kalman Filtering · Make Intuitive_第7张图片

Comparision_fairly.png

[7] https://www.bzarg.com/wp-content/uploads/2015/08/kalflow.png，所采用的取自讲义的素材，都经过了油滴类的矢量化处理，后文与此相同

[8] https://pic4.zhimg.com/80/v2-46b2cd8935b79c519ad0b0380cd60aaf_hd.jpg

[9] Faragher R. Understanding the basis of the kalman filter via a simple and intuitive derivation {lecture notes}[J]. IEEE Signal processing magazine, 2012, 29(5): 128-132.

[10] Attitude and Heading System，AHS，由一套测量、显示和提供航向角和姿态角信号的仪表(如陀螺仪、磁感应传感器)组成，为了给自动驾驶仪、火力控制系统、雷达天线、航空照相机等一系列系统Controller提供更加精准的信息，Kalman Filtering可以作为最优无偏的一种估值器，能对于原始信号进行滤波处理，帮助系统进行姿态解算以及最优控制等任务。

[11] https://github.com/Krasjet/quaternion/

[12] 高显忠, 侯中喜, 王波, 等. 四元数卡尔曼滤波组合导航算法性能分析[J]. 控制理论与应用, 2013, 30(2): 171-177.

[13] 郜丽鹏, 朱嘉颖, 游世勋. 超视距目标跟踪的卡尔曼滤波算法研究[J]. 应用科技, 2019, 46(4): 61-69.

[14] Sabatini A M. Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing[J]. IEEE transactions on Biomedical Engineering, 2006, 53(7): 1346-1356.

卡尔曼滤波剪影__Kalman Filtering · Make Intuitive

铺垫用の引论

(DIS)Advantages总览

"Filtering"的理解

滤波的实质, Vernacularism

"KF"的应用

Kalman Filtering****の详述

Assumption, 事前設定

Modeling Formulation, 実体、正規化

Processing, 具象処理

Kalman Filtering Algorithm:

Prediction:

Updation:

Final EKF, 開拓