算法（三） - 数据结构

列表

列表的存储方式：

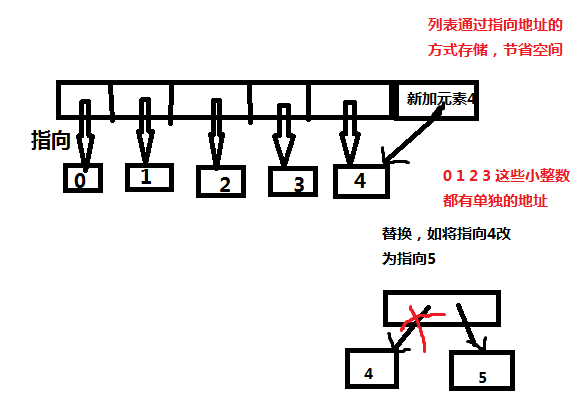
列表的存储方式

列表的操作以及他的复杂度：

append  —— O(1)
insert     —— O(N)
remove  —— O(N)
改          —— O(1)
查( in 操作) —— O(N)

栈（Stack）

后进先出（想象是一叠书）。
用列表就可以实现栈：

stack = []
入栈 = 进制 = 压栈 = push   ->   stack.append()
出栈 = pop                           ->    stack.pop()
取栈顶 = gettop                   ->     stack[-1]

栈的应用：括号的匹配问题，如

{[()]}         匹配
(){}[]         匹配
[](             不匹配
[(])            不匹配
思路，遇到左括号入栈，遇到右括号出栈，最后栈为空就匹配

def check_(s):
    stack = []
    for char in stack:
        # 这里用集合来查，速度更快
        if char in {'(', '[', '{'}:
            stack.append(char)
        elif char = ')':
            if len(stack) > 0 and stack[-1] == '(':
                stack.pop()
            else:
                return False
        elif char = ']':
            if len(stack) > 0 and stack[-1] == '[':
                stack.pop()
            else:
                return False
        elif char = '}':
            if len(stack) > 0 and stack[-1] == '{':
                stack.pop()
            else:
                return False
        if len(stack) == 0:
            return True
        else:
            return False
 

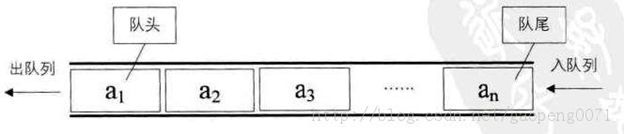
队列（Queue，读Q）

仅允许在列表的一端进行插入，另一端进行删除，进行插入的一端叫队尾（rear），插入动作叫入队 / 进队。进行删除的一端叫队头（front），删除动作叫出队。

队列

队列的使用：

from collections import deque

# 创建队列，li为列表
queue = deque(li)
# 进队
queue.append(x)
# 出队
queue.popleft()

还有，双向队列，即两边都可以出或入，但应用场景少。

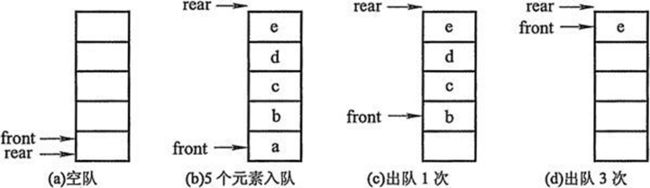
队列的实现原理：
初步假设：列表 + 两个指针。

• 创建一个列表和两个变量，front变量指向队首，rear变量指向队尾。初始时，front和rear都为0。
• 进队操作：元素写到li[rear]的位置，rear自增1。

• 出队操作：返回li[front]的元素，front自减1。

  
  
  

  初步假设

这种方式的问题：
因为出完队，列表存在，导致内存的浪费。

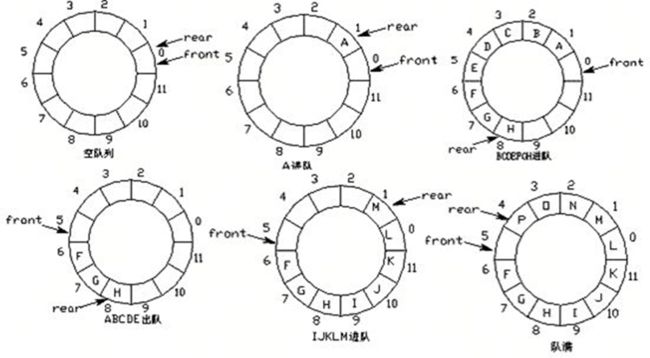
改进：环形队列，即将列表的首尾相连。

改进

实现方式：求余数运算
队首指针前进1：front = (front + 1) % MaxSize
队尾指针前进1：rear = (rear + 1) % MaxSize
队空条件：rear == front
队满条件：(rear + 1) % MaxSize == front

链表

链表中的每一个元素都是一个对象，每个对象称为一个节点。包含有数据域key和指向下一个节点的指针next。通过各个节点之间的相互连接，最终串联成一个链表。
节点定义：

class Node(obj):
    def __init__(self, item=None):
        self.item = item
        self.next = None

头节点，不存元素的节点，以此为头往后找。

单向列表

遍历链表：

def traversal(head):
   curNode = head  # 临时用指针      
   while curNode is not None:        
        print(curNode.data)        
        curNode = curNode.next

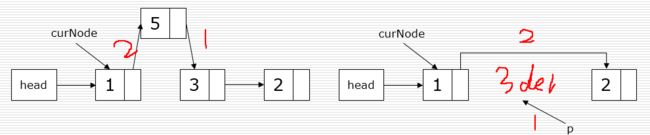
节点的插入，复杂度O(1)：

1 p.next = curNode.next
2 curNode.next = p

节点的删除，复杂度O(1)：

1 p = curNode.next
2 curNode.next = p.next
3 del p

节点的插入与删除

建立链表：

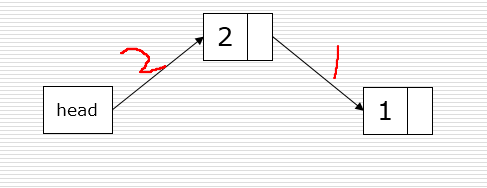
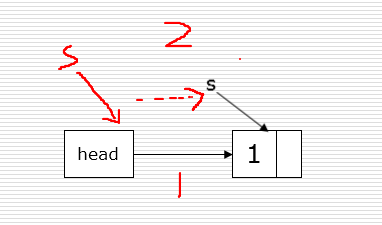
• 头插法，即每次新加的节点的next都是通过拿到头节点的next，然后头节点再重新指向新加的节点的方式创建链表的。所以创建出来的链表是倒序的。

def createLinkList_head(li):
    head = Node()
    for num in li:
        s = Node(num)
        s.next = head.next
        head.next = s
    return head

头插法

• 尾插法，设立一个尾节点，每次新加一个节点，就将新节点赋给尾节点的next，然后让新节点作为尾节点，顺序是正序的。

def createLinkList_tail(li):
    head = Node()
    # tail指向尾节点，刚开始只有一个数，所以tail即是头也是尾。
    tail = head
    for num in li:
        s = Node(num)
        tail.next = s
        tail = s

尾插法

双链表中每个节点有两个指针：一个指向后面节点、一个指向前面节点。用的少。

为什么查时集合与字典比列表快？

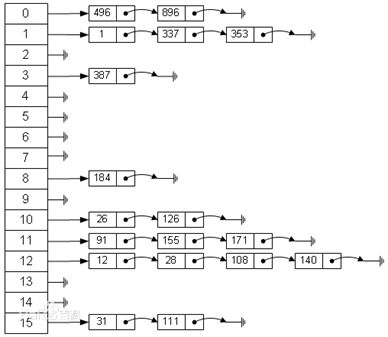
哈希表（Hash Table，又称为散列表），是一种线性表的存储结构。通过把每个对象的关键字k作为自变量，通过一个哈希函数h(k)，将k映射到下标h(k)处，并将该对象存储在这个位置。
例如：数据集合{1,6,7,9}，假设存在哈希函数h(x)使得h(1) = 0, h(6) = 2, h(7) = 4, h(9) = 5，那么这个哈希表被存储为[1,None, 6, None, 7, 9]。
当我们查找元素6所在的位置时，通过哈希函数h(x)获得该元素所在的下标（h(6) = 2），因此在2位置即可找到该元素。

哈希函数种类有很多，这里不做深入研究。
哈希冲突：由于哈希表的下标范围是有限的，而元素关键字的值是接近无限的，因此可能会出现h(102) = 56， h(2003) = 56这种情况。此时，两个元素映射到同一个下标处，造成哈希冲突。

解决哈希冲突：
拉链法，将所有冲突的元素用链表连接
开放寻址法，通过哈希冲突函数得到新的地址

拉链法

在Python中的字典：
a = {'name': 'Alex', 'age': 18, 'gender': 'Man'}
使用哈希表存储字典，通过哈希函数将字典的键映射为下标。假设h(‘name’) = 3, h(‘age’) = 1, h(‘gender’) = 4，则哈希表存储为[None, 18, None, ’Alex’, ‘Man’]
在字典键值对数量不多的情况下，几乎不会发生哈希冲突，此时查找一个元素的时间复杂度为O(1)。