原文:http://www.cnblogs.com/wangnfhy/p/4956711.html
参考:http://theory.stanford.edu/~amitp/GameProgramming/
写在前面的话
无意中在cocoaChina的首页看到了一篇介绍A*算法用swift实现的文章,对A*寻路算法产生了兴趣。在百度谷歌了很多文章后,终于A*算法的流程,同时让我发现了两篇非常好的英文文章:
A* Pathfinding for Beginners
Introduction to A*
第一篇文章是非常好的A*算法入门文章,通读一遍就基本可以用代码实现了;第二篇文章可以说给我带来了震撼,原来算法可以这样讲,推荐大家都看一下。
看完第二篇文章就产生了要学习作者的方式讲一下A*算法的冲动,同时也当是练练手,好久没写javaScript了。
讲解方式也按照一文中的顺序,从最简单的广度优先算法(Breadth-First-Search)、大名鼎鼎的Dijkstra算法到Greed-Best-First-Search算法,最后是A*算法。
(关于A*算法,网上资料很多,A*算法的变种也很多,有兴趣的朋友可以自行搜索,
本文仅对四种常见寻路算法进行简单介绍,若有不合理或错误之处,请谅解并在回复中指出)
广度优先算法
广度优先算法是最简单的寻路算法,算法执行的结果是获得从地图上任意一点S到其他所有可达点的最短路径,这里只考虑上下左右四方向行走的情况,算法流程非常容易理解:
设定搜索起点S,放入openList中;
判断openList是否为空,若为空,搜索结束;若不为空,拿出openList中的第一个节点G;
遍历G的上下左右四个相邻节点N1-N4,对每个节点N,如果N不在openList或closeList中,那么令N的父节点为G,将N放入openList中;如果N已经在openList或closeList中,跳过不处理;
将G放入closeList中,重复步骤2.
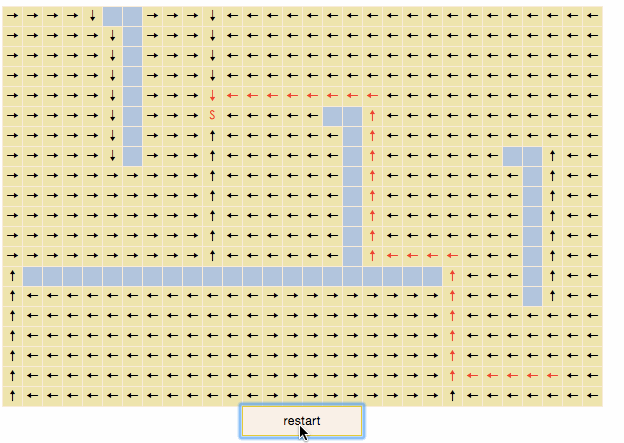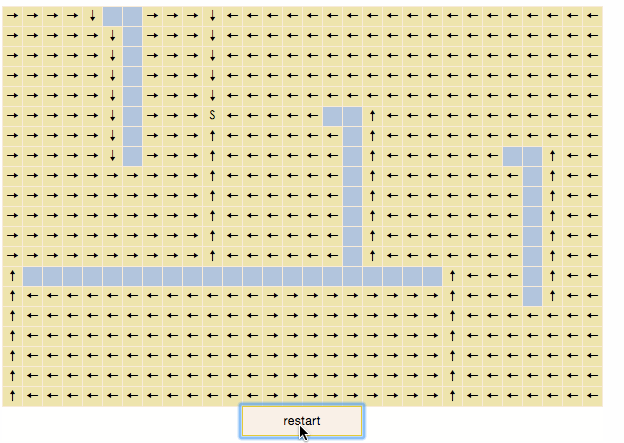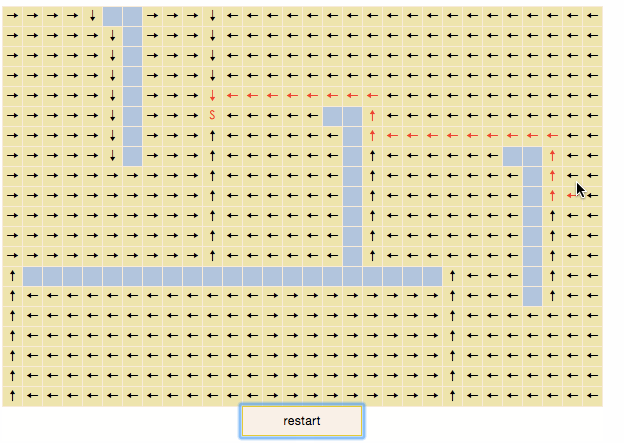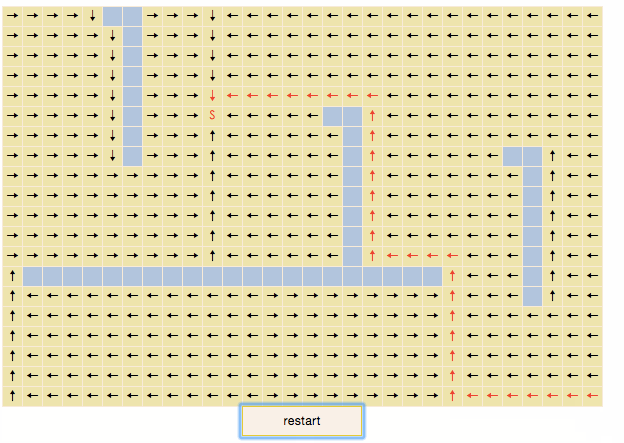
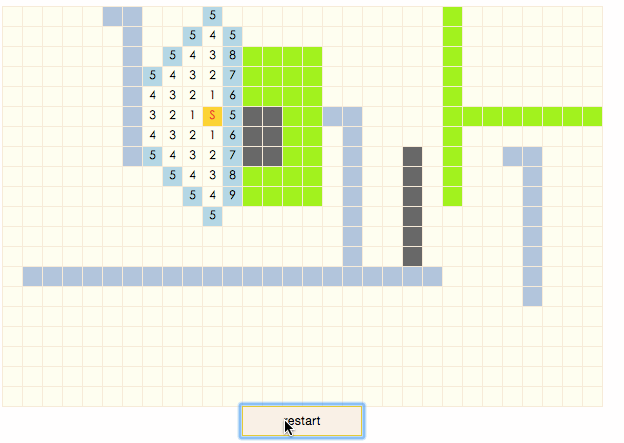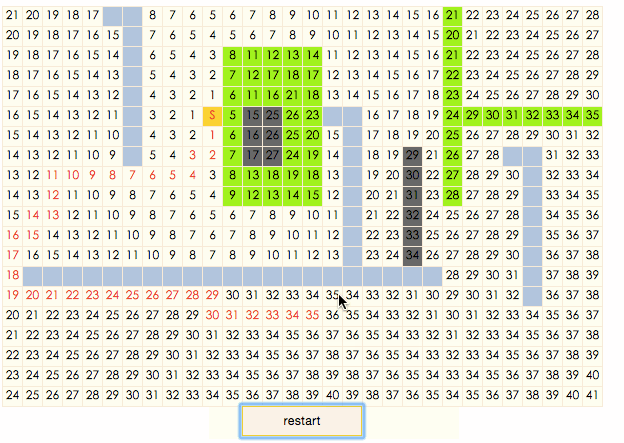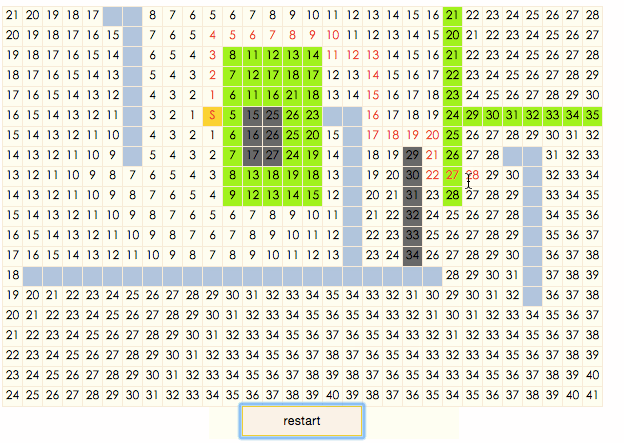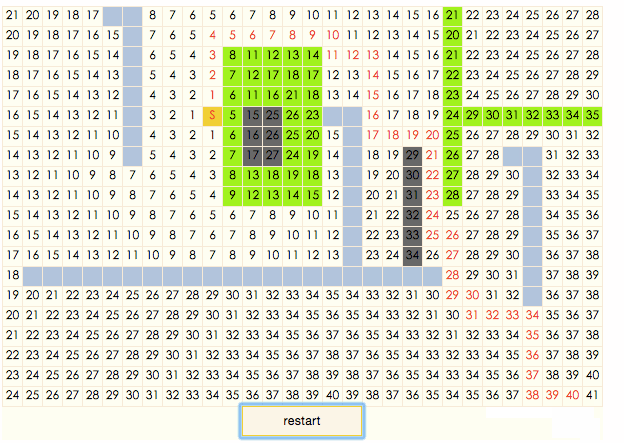
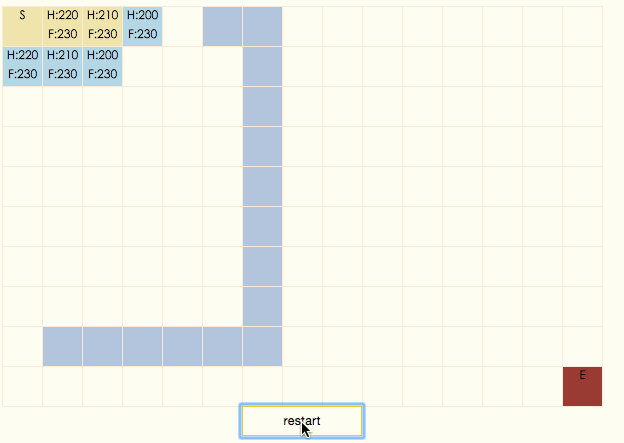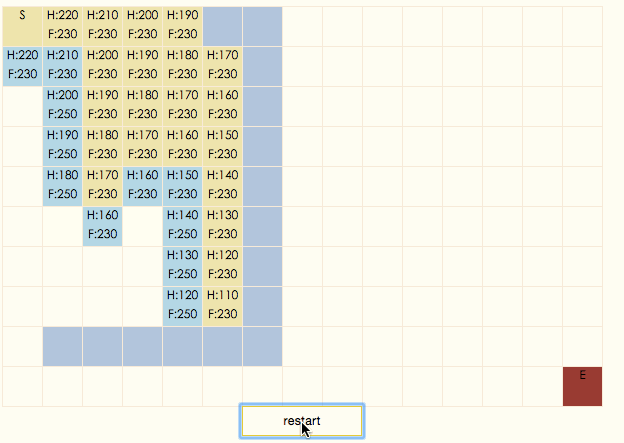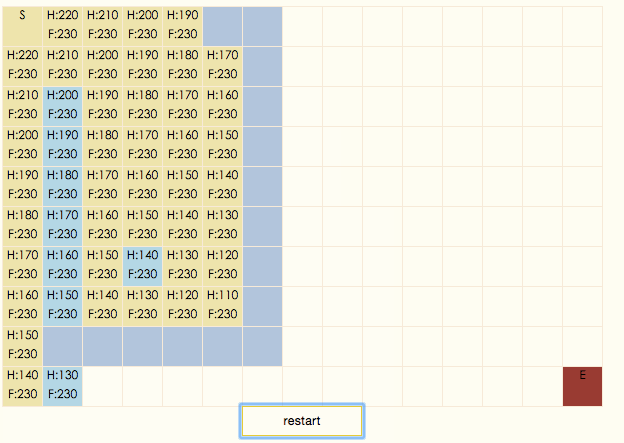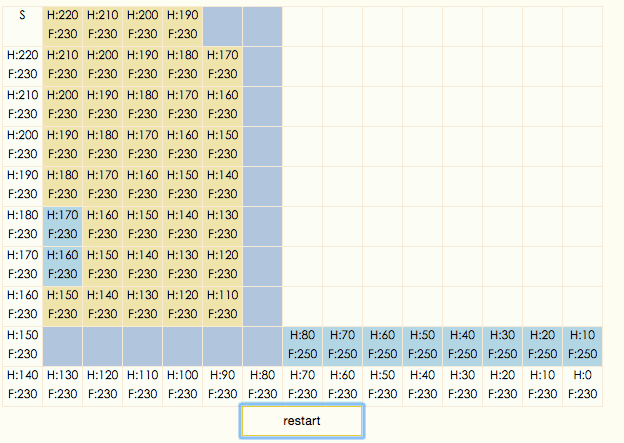
演示gif:
演示程序
蓝色方块是不可通过的,S为扫描的起始点,一层层向外扩展,最终所有可到达的节点都被扫描,这一过程有时被称为“flood fill”。对于每一个被扫描的节点,为其添加一个指向父节点的方向箭头,然后你会发现,从地图上任意一点开始,只要沿着箭头的方向移动,总能走到起始点S,而且走过的路径必然是最短路径之一。
看到广度优先算法,最先想到的应用场景就是塔防,敌人总是从固定的一个或几个出生点出现,向着固定的一个或几个目标移动,我们完全可以在每一关开始前以出生点为起始点遍历整个地图,这样本关中怪物的移动路线就可以确定了。
下面让我们考虑以下场景,地图中存在森林、山岭和平原,角色在这些地形上移动时,移动力消耗是不同的,比如《文明》中。这就要求我们把每一个区块的消耗考虑在内,这时,Dijkstra算法就可以发挥作用了。
Dijkstra算法
在地图内的每个区块移动消耗不同时,Dijkstra算法可以非常方便的找出从地图上某个起始区块到其他所有可达区块的最短路径,这里仍然只考虑上下左右四个方向移动的情况,算法流程如下:
说明:起始区块记作S,从S到当前区块G的总移动消耗记作CG,优先队列openList中数据为(G,CG)(区块,S到当前区块总移动消耗),区块G自身移动消耗记作ZG。
设定起始区块S,将区块S和总移动消耗C=0(记作(S,0))放入openList,其中openList是一个优先队列(PriorityQueue),总移动消耗C越低优先级越高;
判断openList是否为空,如果是空,算法结束;否则,从openList中拿出优先级最高的区块G;
遍历G的上下左右四个相邻区块N1-N4,对每个区块N,如果N已经在closeList中,忽略该区块;如果N不可达,忽略该区块;否则会有两种情况:
如果N不在openList中,那么将(N,CN)放入openList中,其中CN=CG+ZN,既S到N的移动总消耗等于S到G的移动总消耗加上N本身的移动消耗,令N的父节点为G;
如果N已经在openList中,取出(N,CN),仍然计算CN1=CG+ZN,如果CN1小于CN,用(N,CN1)替换openList中的(N,CN),令N的父节点为G;如果CN1大于或等于CN,不做处理。
重复步骤2直至算法结束。
演示gif :
演示程序
蓝色区域不可通过,白色区块代表平原地形,移动一格消耗为1,绿色区块代表森林,移动一格消耗为5,黑色区块带表山脉,移动一格消耗为10。区块中的数字表示从起始点到当前区块的最小移动消耗。从演示程序可以看出,由于优先队列的存在,区块消耗越高,进入closeList的时间越靠后,这与广度优先算法中一层层向外扩展的方式不同。
不难想到,当地图上的所有区块移动消耗相同时,Dijkstra算法就简化为广度优先算法,因为移动总消耗最低的区块总会是当前区块的相邻区块。
在《Introduction to A*》中,作者提出了一个非常有趣的Dijkstra算法的应用,在这里和大家分享下:在某个游戏中,当我希望我的角色更倾向于经过某些区块时(比如经过这些区块可以获得增益效果、道具等等)或者倾向于躲避某些区块时(比如经过这些区块会丢失生命值,或者这些区块上的敌人非常危险),我们可以通过调整这些区块的移动消耗来影响移动路径的产生从而影响角色的移动行为。一片区域上的移动消耗很小时,算法生成的最短路径会倾向于经过这片区域,如gif中要到达森林区块的右侧时,路径没有横穿森林,而是绕着森林边缘走的,反之亦然。
广度优先算法和Dijkstra算法都需要遍历整个地图,而在大多数场景中,我们只需要知道一个点到另一个点的最短路径,下面的Greed-Best-First-Search为我们提供了一个思路。
Greed-Best-First-Search
网上没有找到比较官方的翻译,有人译作“最好优先贪婪算法”,我们暂时这么称呼它。
最好优先贪婪算法与上面两种算法的不同之处在于,它总是尝试向离目标节点更近的方向探索,怎样才算离目标节点更近呢?在只能上下左右四方向移动的前提下,我们通过计算当前节点到目标节点的曼哈顿距离来进行判断。
假设当前节点坐标为(x,y),目标节点的坐标为(x1,y1),曼哈顿距离计算公式如下:
Manhattan_distance = abs(x1-x)+abs(y1-y)
由于曼哈顿距离只在两点之间没有障碍物的情况下才与实际距离相等,一般情况下曼哈顿距离总是小于实际距离。因此,当节点间不存在障碍物时,算法可以保证找出最短路径,但是一旦障碍物出现,最短路径就无法保证了。
算法流程如下:
说明:起始节点记作S,目标节点记作E,对于任意节点G,从当前节点G到目标节点E的曼哈顿距离记作MG,优先队列openList中数据为(G,MG)(节点,当前节点到目标节点E的曼哈顿距离)。
将起始节点S放入openList,openList是一个优先队列,曼哈顿距离越小的节点,优先级越高。
判断openList是否为空,如果为空,搜索失败,目标节点E不可达;如果不为空,从openList中拿出优先级最高的节点G;
遍历节点G的上下左右四个相邻节点N1-N4,如果N在openList或closeList中,忽略节点N;否则,令N的父节点为G,计算N到E的曼哈顿距离MN,将(N,MN)放入openList。
判断节点G是不是目标节点E,如果是,搜索成功,获取节点G的父节点,并递归这一过程(继续获得父节点的父节点),直至找到初始节点S,从而获得从G到S的一条路径;否则,重复步骤2。
演示gif:
演示程序
演示程序中,暗蓝色表示节点是障碍物,土黄色表示节点处于closeList中,淡蓝色表示节点处于openList中,白色表示节点处于搜索出的结果路径上。点击地图上的区块可以重新设置目标节点E。可以看出,当目标节点处于地图左下方时,搜索路径很明显不是最短路径。虽然算法不能保证可以找到最短路径,但当地形不复杂时(如gif中起点和终点间没有障碍物),路径搜索速度是四种算法中最快的。
最好优先贪婪算法虽然不能保证找出最短路径,但为我们提供了一个思路,A*算法就是Dijkstra算法与最好优先贪婪算法结合后得到的算法。
A*算法
A*算法与最好优先贪婪算法一样都通过计算一个值来判断探索的方向。对于节点N,计算公式如下:
F(N)=G(N)+H(N)
其中G(N)就是Dijkstra算法中计算的,从起点到当前节点N的移动消耗,而H(N),在只允许上下左右移动的前提下,就是最好优先贪婪算法中当前节点N到目标节点E的曼哈顿距离。因此,当节点间移动消耗非常小时,G对F的影响也会微乎其微,A*算法就退化为最好优先贪婪算法;当节点间移动消耗非常大以至于H对F的影响微乎其微时,A*算法就退化为Dijkstra算法。
算法流程如下:
说明:起始节点记作S,目标节点记作E,对于任意节点P,从S到当前节点P的总移动消耗记作GP,节点P到目标E的曼哈顿距离记作HP,从节点P到相邻节点N的移动消耗记作DPN,用于优先级排序的值F(N)记作FP。
选择起始节点S和目标节点E,将(S,0)(节点,节点F(N)值)放入openList,openList是一个优先队列,节点F(N)值越小,优先级越高。
判断openList是否为空,若为空,则搜索失败,目标节点不可达;否则,取出openList中优先级最高的节点P;
遍历P的上下左右四个相邻接点N1-N4,对每个节点N,如果N已经在closeList中,忽略;否则有两种情况,
如果N不在openList中,令GN=GP+DPN,计算N到E的曼哈顿距离HN,令FN=GN+HN,令N的父节点为P,将(N,FN)放入openList;
如果N已经在openList中,计算GN1= GP+DPN,如果GN1小于GN,那么用新的GN1替换GN,重新计算FN,用新的(N,FN)替换openList中旧的(N,FN),令N的父节点为P;如果GN1不小于GN,不作处理。
将节点P放入closeList中。判断节点P是不是目标节点E,如果是,搜索成功,获取节点P的父节点,并递归这一过程(继续获得父节点的父节点),直至找到初始节点S,从而获得从P到S的一条路径;否则,重复步骤2;
演示gif:
演示程序
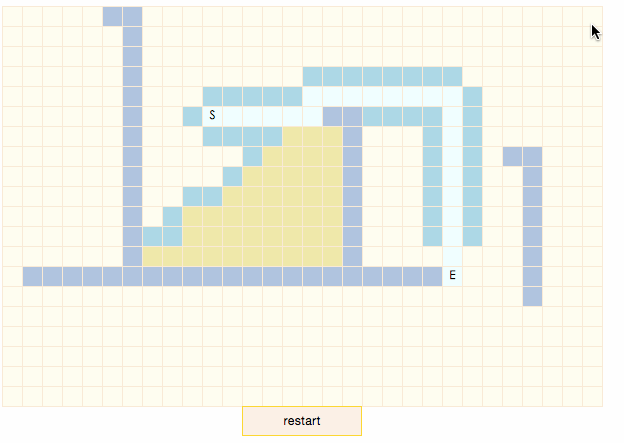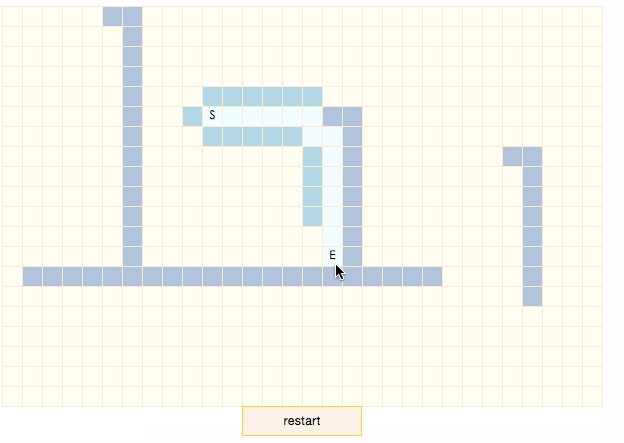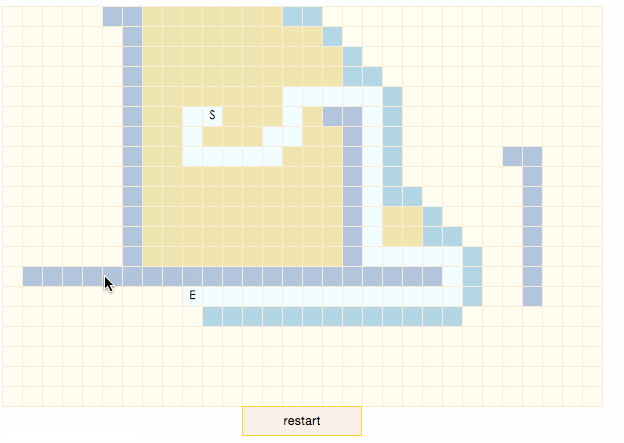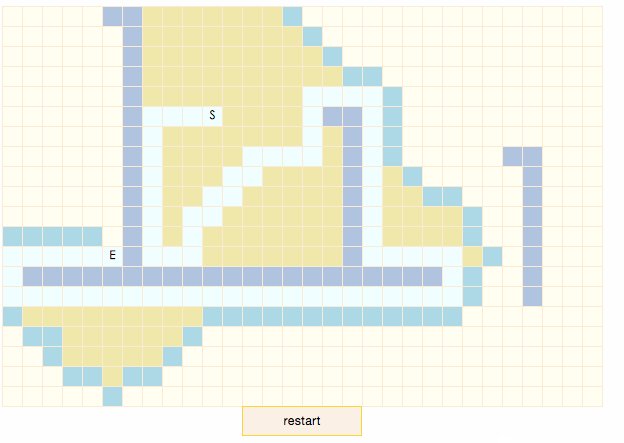
演示gif中,土黄色表示节点在closeList中,淡蓝色表示节点在openList中,深蓝色表示节点不可通过,白色表示节点在搜索出的结果路径上。可以看出,A*算法总是设法保证搜索路径上的F值保持不变。
在继续测试演示程序时,我发现了一个问题:
由于我用JS开发的上述演示程序,没有趁手的优先队列,所以用Array客串了一把,每次取值时根据F值进行倒序排序,取队列末尾的值。从gif中可以看出,算法执行的并不完美,我们当然希望A*算法在简单环境下能够拥有和最好优先贪婪算法一样的运行速度,但我的A*算法却出现了无用的扫描,并不在搜索结果上的区域也参与了计算。怎样避免这一情况呢?
首先想到的当然是改进我的优先队列,但这有点麻烦啊,别着急,有更简单的方法,这个方法和接下来要了解的启发式算法有关。
关于最优选择贪婪算法和A*算法中的曼哈顿距离的运用属于启发式算法(Heuristic Algrathm)的一种,这也是A*算法公式F=G+H中H的由来。
这里摘抄一段《Introduction to A*》的作者在另一篇文章《Heuristic》中的一小段,讲述H(n)如何影响A*算法的行为。
At one extreme, if h(n) is 0, then only g(n) plays a role, and A* turns into Dijkstra’s algorithm, which is guaranteed to find a shortest path.
If h(n) is always lower than (or equal to) the cost of moving from n to the goal, then A* is guaranteed to find a shortest path. The lower h(n) is, the more node A* expands, making it slower.
If h(n) is exactly equal to the cost of moving from n to the goal, then A* will only follow the best path and never expand anything else, making it very fast. Although you can’t make this happen in all cases, you can make it exact in some special cases. It’s nice to know that given perfect information, A* will behave perfectly.
If h(n) is sometimes greater than the cost of moving from n to the goal, then A* is not guaranteed to find a shortest path, but it can run faster.
At the other extreme, if h(n) is very high relative to g(n), then only h(n) plays a role, and A* turns into Greedy Best-First-Search.
翻译如下:
一种极端情况是,当H(n)=0时,只有G(0)有效,此时A*算法变为Dijkstra算法,可以保证找到最短路径。
如果H(n)总能保证不大于从n到终点的实际距离,那么A*算法就可以保证找到最短路径(如上面演示程序中,在智能上下左右四方向移动的前提下,曼哈顿距离总是小于或等于实际距离)。H(n)相比实际距离越小,A*算法需要探索的节点就更多,性能就会更差一些。
如果H(n)与n到终点的实际距离相等,那么A*算法就可以一直保持探索路径在最优路径上而不需要探索额外的节点,使得算法执行非常快。虽然这是理想状态下的场景,但是如果提前对地图进行分析,我们还是可以保证A*算法在近似理想的状态下工作。(关于A*算法的优化后面会讲到)
另一种极端情况是,当H(n)相对于G(n)非常大时,只有H(n)有效,A*算法就会变成最优选择贪婪算法,不能保证找到最短路径。
回到刚才的问题,这个简单的方法就是修改我们的H(n),新的曼哈顿距离公式为
Manhattan_distance =abs(x1-x)+abs(y1-y)*1.01
我们对上下方向的距离进行了轻微的调整,效果如何呢?
演示程序
允许斜方向移动演示程序
可以看到,扫描过程非常高效,所有closeList中的节点都出现在了结果路径上。这是因为A*算法会沿着F值变小的方向搜索,由于曼哈顿公式的调整,原本F值相等的节点不再想等,同一列由上到下递减,这就产生了gif中的现象,结果路径总是先向下走,直到和目标节点同一行后,再向右走。
关于四种算法的选择
虽然最优选择贪婪算法只在特定情况下才可以找到最短路径(没有障碍物、没有地形移动消耗差异),但是它的运行速度是最快的。如果情况允许,优先使用本算法。
当需要知道地图上某个点到所有其他点的最短路径,或者反过来,地图上所有点到某个点的最短路径时,选择广度优先算法(各区块移动消耗相同)或Dijkstra算法(各区块移动消耗不同)。
在一般情况下,使用A*算法总是正确的。
A*算法的一般优化
在情况允许的前提下,在生成地图或者加载地图时,记录地图上的特征区域。特征区域分为两类:
第一类是不可到达区域,当目标点位于不可到达区域时,以上四类算法都会进行全图扫描,这绝对是资源的极大浪费;
第二类是导航点,所谓导航点,就是地图上两个区域间移动的必经之路,例如游戏中两片陆地被河流分割,中间一座小桥,这座桥就是导航点,当需要找到从一片大陆到另一片大陆的最短路径时,可以先算出起点到这座桥的最短路径,再算出这座桥到终点的最短路径,那么两者加起来就是起点到终点的最短路径。同样的道理,如果地图分为两层,楼梯的部分也是导航点。