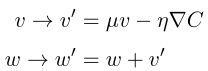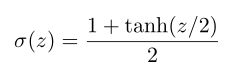《neural network and deep learning》题解——ch03 其他技术（momentun，tanh）

http://blog.csdn.net/u011239443/article/details/77848503

问题一

• 如果我们使⽤ µ > 1 会有什么问题？
• 如果我们使⽤ µ < 0 会有什么问题？

如果我们使⽤ µ > 1，∇C趋近于0时，v依旧会越来越大。如果我们使⽤ µ < 0，∇C趋近于0时，v会变为梯度的反方向。

问题二

增加基于 momentum 的随机梯度下降到 network2.py 中。

增加 b_velocity 和 w_velocity

    def default_weight_initializer(self):
        self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
        self.weights = [np.random.randn(y, x)/np.sqrt(x)
                        for x, y in zip(self.sizes[:-1], self.sizes[1:])]
        self.b_velocity = [np.random.randn(y, 1) for y in self.sizes[1:]]
        self.w_velocity = [np.random.randn(y, x)/np.sqrt(x)
                        for x, y in zip(self.sizes[:-1], self.sizes[1:])]

增加参数 µ （mu）

    def SGD(self, training_data, epochs, mini_batch_size, eta,
            lmbda = 0.0,mu = 1.0,
            evaluation_data=None,
            monitor_evaluation_cost=False,
            monitor_evaluation_accuracy=False,
            monitor_training_cost=False,
            monitor_training_accuracy=False):
        ......
        for j in xrange(epochs):
            random.shuffle(training_data)
            mini_batches = [
                training_data[k:k+mini_batch_size]
                for k in xrange(0, n, mini_batch_size)]
            for mini_batch in mini_batches:
                self.update_mini_batch(
                    mini_batch, eta, lmbda,mu, len(training_data))
             ......

    def update_mini_batch(self, mini_batch, eta, lmbda,mu, n):
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]

        self.w_velocity = [mu*v-(eta/len(mini_batch))*nw for v, nw in zip(self.w_velocity, nabla_w)]
        self.weights = [(1-eta*(lmbda/n))*w + v for w, v in zip(self.weights, self.w_velocity)]
        self.b_velocity = [mu*v-(eta/len(mini_batch))*nb for v, nb in zip(self.b_velocity, nabla_b)]
        self.biases = [b + v for b, v in zip(self.biases, self.b_velocity)]

问题三

证明公式 (111)

$\large \frac{1+ tanh(z/2)}{2} = \frac{1 + (e^{z/2} - e^{-z/2})/(e{z/2} + e^{-z/2})}{2} = \frac{e^{z/2}}{e{z/2} + e^{-z/2}} = ^{分子分母除以 e^{z/2}} \frac{1}{1+e^{-z}}$

这里写图片描述