多因一果
——《小学数学这样教》读书笔记13
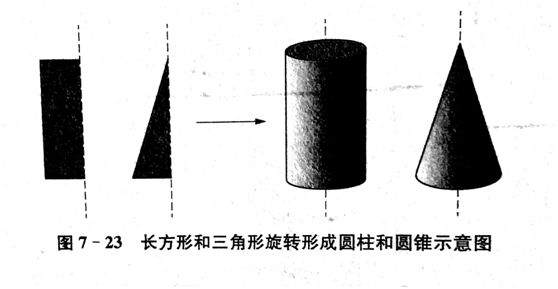
把一个长方形绕一条边旋转得到一个圆柱,同理把这个长方形一分为二得到一个直角三角形,绕其直角边旋转得到一个圆锥。按我们的直观经验,旋转前的三角形是长方形面积的一半,而且它们又是同步旋转,因此,圆锥的体积就应该是圆柱的一半呀?可实际上为什么不是一半呢?原来,这里涉及了因果关系。有的现象是一因一果,而有的现象则是多因一果。那么,在数学中是如何来描述因果关系呢?
从某种意义上说,数学是一门研究“关系”的学问。比如说,认识自然数“2”,实际上就是认识它与“1”的关系。所谓长方形面积公式实际上就是表达长方形的面积与边的关系。
一般来说,关系分为两大类。第一类叫做“相合与相离”的关系,概念的种属关系就属于这一类。第二类叫做“依赖与制约”的关系,因果关系就属于这一类。在研究因果关系的时候,往往有两种思路,一种是通过原因寻找结果,叫做“执因寻果”;另一种是通过结果寻找原因,叫做“执果寻因”。
比如对于一个正方形,如果把利用边长求周长叫做“执因寻果”,那么知道周长求边长就是“执果寻因”,这两个问题都是不难解决的,原因在于这是“一因一果”的问题。(因为正方形的四条边都相等。)
对于长方形来说,如果已知长方形的长和宽,那么可以求出周长;反过来,如果知道长方形的周长,要想求出这个长方形的长和宽,就会出现多种答案的不确定现象,因为这是一个“二因一果”的问题。
由此,想到福建罗鸣亮老师在讲“圆的认识”这节课时的导入阶段:先出示平面图形长方形,正方形等,然后询问要描述它们的大小,要用几个数据;再追问,你觉得要描述圆的大小,要几个数据呢?这里就涉及到了几因几果的关系。在平时练习中,经常有这样的判断题,让孩子觉得很是困惑。比如:
1.正方形的周长越大面积就越大。(√)
2.长方形的周长越大面积就越大。 (×)
3.圆的周长越大面积就越大。(√)
也有的时候,会把面积与周长调换过来出判断题。可以发现,这里面也有着几因几果的关系,对孩子们的数学理解要求很高。现实教学中,常常把那些不是靠理解来学习的孩子弄得头昏脑涨的。当然,真的理解了的孩子,会说道:“圆与正方形是一个条件就可以决定的事情,而长方形要两个因素相互调节才能解决问题。”从这一块也再次说明:学习数学重在理解,理解后的数学,有一条清晰的思维线。
回到为什么等底等高的圆锥体积不是圆柱体积的一半这个问题中来,这实质上是二因一果的问题。换句话说,不能仅仅考虑旋转前的面积相等这一个因素,还要考虑旋转体到旋转轴的距离因素。
1. 初步解释
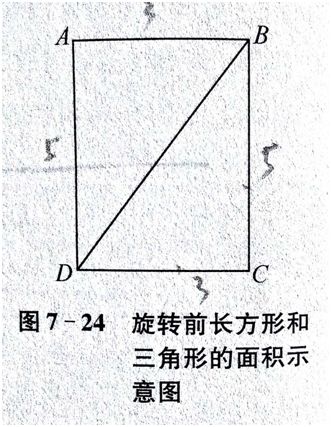
如上图7-24长方形的BC边长度为5cm,AB边的长度为3cm。假设这个长方形围绕AB边旋转一周得到一个圆柱,那么不难计算出这个圆柱的体积是75π,再假设图7-24长方形ABCD是围绕BC边旋转一周也得到一个圆柱,能算出这个圆柱的体积是45π.我们发现,同样的长方形,围绕不同的边旋转出来的圆柱体积是不同的。这就充分说明了旋转前面积的大小不是制约旋转后体积大小的唯一原因,还旋转面与到旋转轴的距离有关. 如果把旋转后的体积看作因果关系的结果,那么这个结果的产生不是一个原因,至少有以上2个原因。
古希腊后期有一位数学家帕普斯,在他所著的《数学汇编)中记载了这样一条定理:如果一个平面封闭图形绕图形的某一条直线旋转一周,则旋转出来的形体的体积等于初始面的面积乘以其重心所转过的圆周长度。这一定理显示出,旋转体的体积是如下两个量的乘积:第一是旋转前的面积;第二是旋转面的重心旋转的圆周长度。圆周长度是由半径的长度决定的,因此可以说旋转体的体积的大小由旋转面的面积和旋转面重心到旋转轴的距离这样两个因素决定的。
2. 图形的重心
这里说的平面图形的重心,是一个物理学中的概念。以上图长方形ABCD为例(AB=3,BC=5),重心BC边的距离1.5cm,重心到AB边的距离为2.5cm,如果这个长方形围绕BC边旋转,那么帕普斯斯定理中所说的重心所旋转的圆周长度就是“2×1.5×π=3π”,长方形面积是“3×5=15”依据帕普斯定理,旋转后圆柱的体积就是“3π×15=45π”,与前面计果是一致的。如果这个长方形围绕AB边旋转,同样得到旋转后的圆柱体积为(2×2.5×π)×(3×5)=75π。两个答案不一样的原因就是重心到旋转轴的距离不一样。
圆锥是由直角三角形绕直角边旋转而成的,因此,下面再来看三角形的重心情况。
经过一系列的转化(小学六年级的孩子是可以理解这种面积转化过程的),可以把三角形重心概括为这样两句话:
(1)任意三角形的重心是三条中线的交点;
(2)任意三角形的重心位于每一条中线靠近底边的三等分点处。
3.疑惑的解释
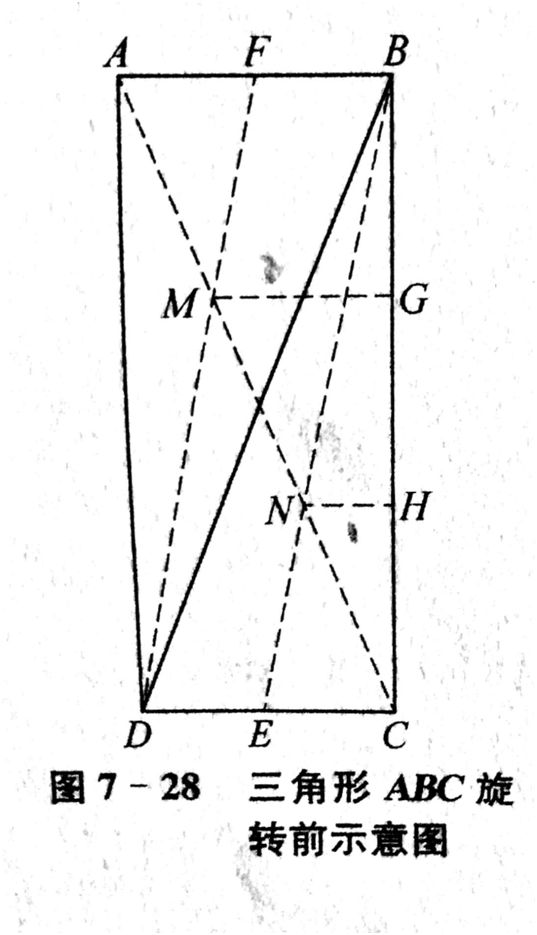
如上图,长方形中添加上对角线AC,三角形ABD的中线DF和三角形BDC的中线BE。这样就分别找到了三角形BCD的重心N和三角形ABD的重心M。重心N到旋转轴BC的距离是线段NH的长度,重心M到旋转轴BC的距离为线段MG的长度。这两个距离是不一样的。
利用一点初中“相似三角形对应边成比例”的知识可以知道,线段NH的长度是线段AB长度的三分之一,线段MG的长度是AB长度的三分之二,因此三角形ABD的重心到旋转轴的距离就是三角形BDC重心到旋转轴距离的2倍。
由于任意一个圆的圆周长度与这个圆的半径成正比例,因此三角形ABD的重心旋转的圆周长度就是三角形BDC的重心旋转的圆周长度的2倍。两个三角形面积相等,重心的旋转半径是2倍关系,根据帕普斯定理,三角形ABD旋转出来的体积就是三角形BDC旋转出来的体积的2倍。把三角形BDC旋转后的体积看成1,则三角形ABD旋转后的体积就是2,总份数就是3。因此长方形ABCD旋转出来圆柱的体积就是三角形BDC旋转出来圆锥体积的3倍,反过来圆锥体积就是圆柱体积的三分之一。至此,不仅解释了“为何不是二分之一”的问题”,还解释了“为何是三分之一”。
由于要用到物理学中的图形的重心,初中的相似比,小学生还是很难彻底弄明白。当然,到了大学,用微积分就更好理解圆锥的体积公式了。但是,知识的缺乏并不妨碍小学生去探究知识背后的道理,数学应该要促进孩子去探讨,深究……