说明: 最近在看Ng的DL课程,感觉说的非常好,浅显易懂!
本来打算记录一下自己的学习过程,网上几个大神总结的太完美了,根本没必要自己去写了,而且浪费时间~~
网易地址:http://mooc.study.163.com/course/2001281002?tid=2001392029#/info,我是用1.75倍的速度看的,可能之前看过ML的缘故吧,就感觉很简单了。
大神博客地址:http://kyonhuang.top/Andrew-Ng-Deep-Learning-notes/#/
https://redstonewill.github.io/2018/03/29/39/
http://binweber.top/2017/09/28/deep_learning_3/
https://zybuluo.com/hanbingtao/note/541458
后面干脆不看视频了,还是有点慢了。
现在直接看别人笔记,代码撸起来,最后TF去搭建框架。。。
难点记录一:
改善深层神经网络,其中的动量V的如何引入?
首先理解一下物理中动量的相关概念,M1V1 = M2V2动量守恒定律,说的就是速度带有方向性,当质量不变的时候(别想爱因斯坦的光速,就想牛顿世界),速度在某一个方向上是守恒的,在进一步说明了速度的方向性(矢量)。
再说一下这个速度V怎么去求解的?其实速度就是θ的梯度dθ,初始的速度V1=dθ1,第一步的V1和V2相同(方向和大小),所以第一步走的很远,之后就按照公式去计算了,后面的就不说了,直接看Ng的文档~~
难点记录二:
加速神经网络训练的几种方法联系和由来?
这里本来自己已经明白了,还是组织语言没有莫凡大神的好,干脆直接引用他的话来叙述吧!
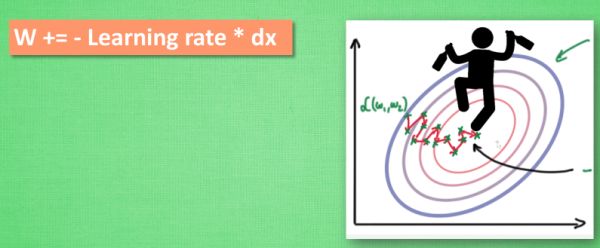
下面一张图描述了各种加速算法路径,这里我们不讨论每个算法的改进,如:正则化,归一化,惩罚因子,局部全局等
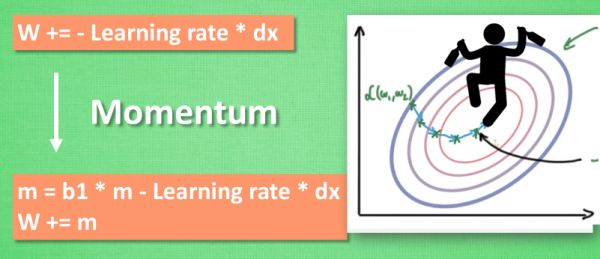
Momentum动量更新法:
大多数其他途径是在更新神经网络参数那一步上动动手脚. 传统的参数 W 的更新是把原始的 W 累加上一个负的学习率(learning rate) 乘以校正值 (dx). 这种方法可能会让学习过程曲折无比, 看起来像 喝醉的人回家时, 摇摇晃晃走了很多弯路.
所以我们把这个人从平地上放到了一个斜坡上, 只要他往下坡的方向走一点点, 由于向下的惯性, 他不自觉地就一直往下走, 走的弯路也变少了. 这就是 Momentum 参数更新.
补充:说白了就是加入了上一次权重W的作用(也可以说是上一次的梯度,因为权重就是梯度计算来的),因为不能总看当下,也要适当的回顾!这里的回顾是利用加减进行的!
AdaGrad:
这种方法是在学习率上面动手脚, 使得每一个参数更新都会有自己与众不同的学习率, 他的作用和 momentum 类似, 不过不是给喝醉酒的人安排另一个下坡, 而是给他一双不好走路的鞋子, 使得他一摇晃着走路就脚疼, 鞋子成为了走弯路的阻力, 逼着他往前直着走. 他的数学形式是这样的. 接下来又有什么方法呢? 如果把下坡和不好走路的鞋子合并起来, 是不是更好呢? 没错, 这样我们就有了 RMSProp 更新方法.
补充:其实这里还是看了上一次的梯度,不过这是运用的是乘除进行的!
RMSProp 更新方法:
有了 momentum 的惯性原则 , 加上 adagrad 的对错误方向的阻力, 我们就能合并成这样. 让 RMSProp同时具备他们两种方法的优势. 不过细心的同学们肯定看出来了, 似乎在 RMSProp 中少了些什么. 原来是我们还没把 Momentum合并完全, RMSProp 还缺少了 momentum 中的 这一部分. 所以, 我们在 Adam 方法中补上了这种想法.
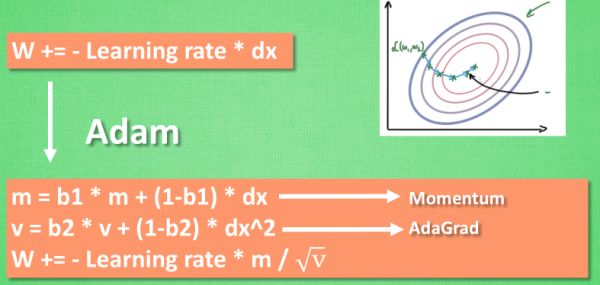
Adam更新方法:
计算m 时有 momentum 下坡的属性, 计算 v 时有 adagrad 阻力的属性, 然后再更新参数时 把 m 和 V 都考虑进去. 实验证明, 大多数时候, 使用 adam 都能又快又好的达到目标, 迅速收敛. 所以说, 在加速神经网络训练的时候, 一个下坡, 一双破鞋子, 功不可没.
总结:说白了每个优化算法都是利用梯度,只不过利用梯度的方式不同,有人会问既然都是利用W去做优化,为什么还有那么多区别呢?你如果看到PID算法就知道了,对于一个误差可以用 比例/积分/微分 去做,但是结果却不一样。废话不多说,这里需要自己理解一下。
难点记录三:
resnet(残差网络)的作用及由来?
这个问题网上说的都是一知半解,我也看了很久的资料才大概了解一点。
先看以下的两篇文章,了解一下工作机理及来龙去脉:
https://www.zhihu.com/question/53224378,
https://www.jianshu.com/p/e58437f39f65,
通俗易懂的解释:
1.社会越来越复杂,越复杂的东西越能证明一个人的智慧。那么神经网络的的层数越多,越能解决复杂的问题(运用的特征越多),这一点毋庸置疑吧?那么我们是不是可以理解,越多层的神经网络计算的精度越好呢?答案是否定的,实验证明层数达到一定范围精度就会下降,物极必反~~
2.那能不能这样,比如100层的网络可以很好的解决一个问题,假设精度为0.01.那我现在用了250层的网络,前面100层参数和之前的100层一样,后面150层直接用恒等函数y=x,完美解决?实验证明这样不行的,层数太多了,去拟合150个y=x难度很大。
3.当然作者还通过BN去减少梯度消逝的现象,效果很不明显。
4.我们回顾2和3提出的问题,首先不是数据的原因(BN没办法解决),再次和层数关系不是根本原因(理论说明层数越多,效果应该越好才对),最后查看3提出的问题,拟合150个y=x难度太大?既然不是数量原因,那就是y=x太难拟合了吗?
5.试着降低拟合难度,降低到y=k(k为一个常数),降低到y=0 ?如果这两个函数再拟合不出来,那就没办法了~~
6.我们的目的是拟合到y = x ,现在中间加一个 y = p + x , 那么我们现在的目的就是让p=0就可以了。实验证明效果很好~~
周密解释:
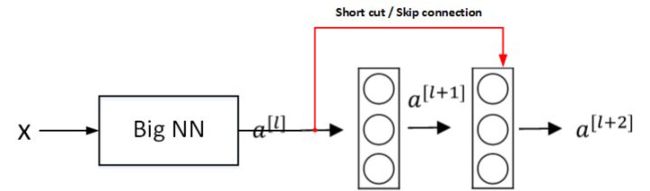
假设有一个大型神经网络,其输入为 X,输出为 a[l]。给这个神经网络额外增加两层,输出为 a[l+2]。将这两层看作一个具有跳远连接的残差块。为了方便说明,假设整个网络中都选用 ReLU 作为激活函数,因此输出的所有激活值都大于等于 0。
则有:![]()
当发生梯度消失时,![]() ,
,![]() ,则有:
,则有:
![]()
因此,这两层额外的残差块不会降低网络性能。而如果没有发生梯度消失时,训练得到的非线性关系会使得表现效果进一步提高。
注意,如果![]() 与
与 ![]() 的维度不同,需要引入矩阵 Ws与
的维度不同,需要引入矩阵 Ws与 ![]() 相乘,使得二者的维度相匹配。参数矩阵 Ws既可以通过模型训练得到,也可以作为固定值,仅使
相乘,使得二者的维度相匹配。参数矩阵 Ws既可以通过模型训练得到,也可以作为固定值,仅使 ![]() 截断或者补零。
截断或者补零。
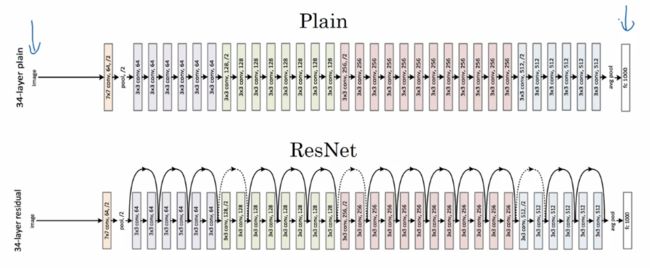
上图是论文提供的 CNN 中 ResNet 的一个典型结构。卷积层通常使用 Same 卷积以保持维度相同,而不同类型层之间的连接(例如卷积层和池化层),如果维度不同,则需要引入矩阵 Ws。
难点记录四:
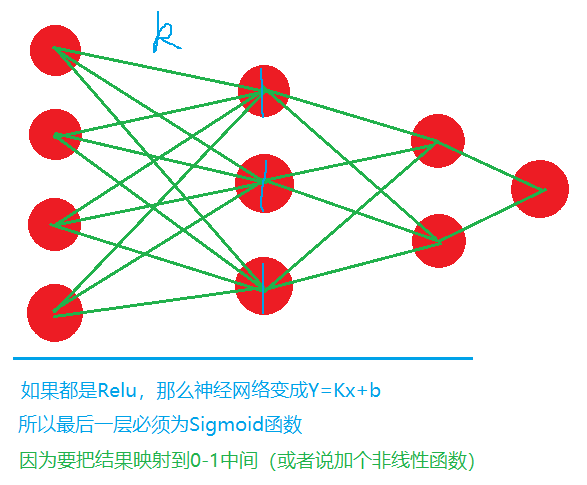
为什么ReLu比Sigmoid好?为什么不能全部用Relu?
1.首先我们解决第一个问题,从计算量和优化效果去理解!
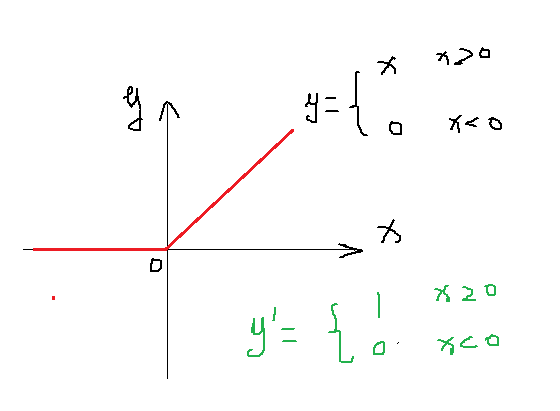
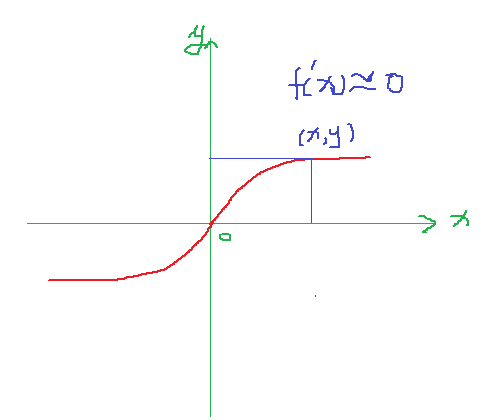
从上面的两幅图可以看出,ReLu函数的导数很简单,而且倒数为1很容易计算,而Sigmoid在(X,Y)处的导数接近于0 ,给梯度下降计算带来麻烦,也容易陷入局部最优!
好了?我们再来回答第二个问题~~
2.学到后面的问题时候,我们可以分类问题花费两类:A.单分类。B.多分类。
单分类:
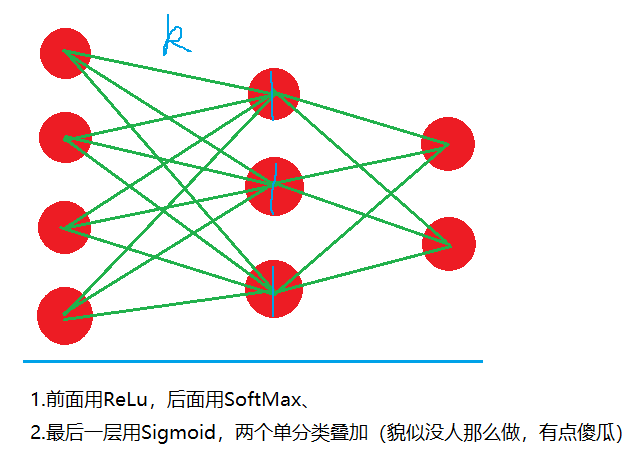
多分类: