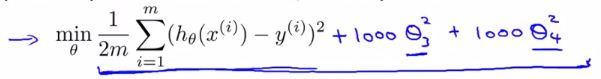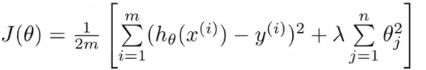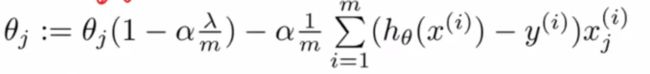MulticlassClassification and Representation
这周开始讲Classification问题啦。分类问题应用非常广泛。比如识别欺诈邮件、信用欺骗、分辨恶性肿瘤等等。
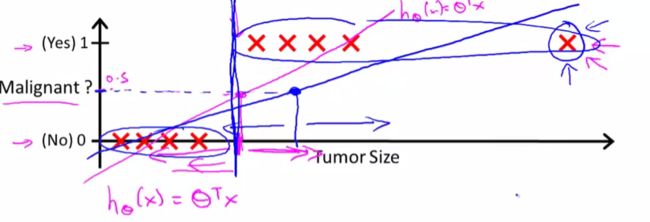
分类函数可以从线性回归出发,对线性回归的prediction做阈值划分,阈值上下用0 1 表示。当然这并不是一个合适的方法,误判的概率是很大的。
因此,Logistic Regression横空出世。LR的值域处于0-1之间,所以能很好地克服线性回归的劣势。
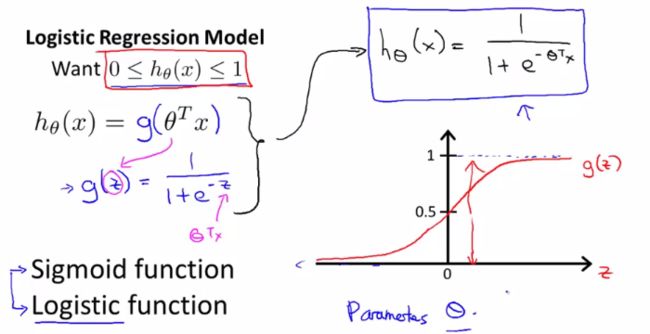
如Andrew所介绍,Logistic回归的核心要点是采用了Sigmoid函数,S函数,也就是slide里的g(z),很容易可以推断出当z的定义域在实数范围内时,S函数的值域在0到1之间,而且转换点在z取0附近,如右图。应用初等数学复合函数的思想就可以知道,当我们构建了一个S函数之后,把z替换为之前的linear regression model,那么新的假设不就可以很好地将prediction落在0-1之间了么,呵呵呵。S函数在classification问题的应用或许已经成为业界共识,但是遇到问题解决问题过程中涉及的巧妙转换和建模方法,值得我们思考和积累。
接下来对Logistic值的解释就更合理了,概率!Andrew还是以tumor为例,当h(x)=0.7的时候,我们可以认为有70%概率这个tumor是恶性的。使用概率统计的标志符可以记为:
htheta(x)=P(y=1|x;theta) % probability that y =1, given x, parameterized by theta
V3, Decision Boundary
Andrew首先介绍了一个简单的判别方法,从sigmoid函数值域可以看出,当x小于0,y有大于50概率为0,反之为1.所以,可以对复合函数中内层函数的值域进行简单的判定,若theta'x小于0,那么置htheta(x)=0; thata'x>=0, hthata(x)=1.
随后介绍了一个具体的例子来说明decision bounday,如下图所示,当我们通过某种手段fit出theta0-2的最优估计后,可以看到htheta所代表的直线将左右两侧的样本点进行了较好的分割,那么目前htheta所代表的直线就是decision boundary,从概率的角度来说,也就是50%分割线。注意decision boundary是hypothesis和parameter的性质,而不是样本性质。
当然boundary可以有各种各样的形式,比如可以用二元二次的假设,那么boundary可以是个圆 抛物线 双曲线,也可以是更复杂的多项式,那就是各种扭来扭去的曲线了。
Logistic Regression Model
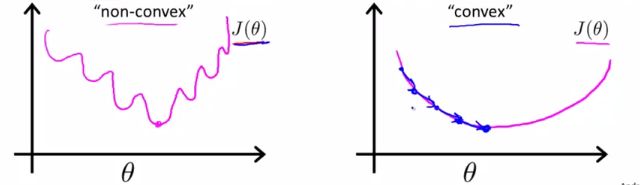
Andrew首先介绍了如果采用linear regression的cost function形式用于logistic regresion是不可以的,因为这将使得cost function成为"non-convex"(非凸)函数。
Andrew给出的sigmoid函数的cost function居然具有如此魔性的结构,当然用梯度下降是没法找到全局最小值的了。不过为什么函数曲线真的如此魔性么?视频中并没有具体推导,我们可以简单推想一下:假定cost function中y为0,这样就退化成考虑sigmoid函数的平方形式具有什么样的曲线特征。带入极限可以知道theta->-inf和+inf的时候,极限与S函数一样都是0和1,问题是中间怎么变的,简单替换了下发现其实在theta属于0~+inf是单调的,没有继续细究y存在是怎样的情况,这里留个open question。
我们对Logistic Regression设计的cost function非常有趣:
非常有意思,我们假定观测结果为1的话,也就是说事实上发生了事件,那么当我们预报完全失败的时候,也就是认为发生事件的概率为0的话,cost function会倾向于无穷大,这是个非常严厉的惩罚,而当很好的预报时,cost function则为minimum 0.当y=0时,通过log函数的变换也可以看出,效果是一致的。这样设计cost function一则简单,二则拥有了非常有效的性质。这种构建思想非常了不起。
V2介绍简化cost function和梯度下降,这里又一次展现了牛逼的构建技巧,因为观测结果y的存在无非只有0和1两种形态,因此可以将cost function分段形式合并到一起为:
Andrew随后介绍了这样构建CF的原因,通过最大似然估计(maximum likelihood estimation)推导可知道这一函数一来可以高效地为不同的model找到参数化数据(?没有明白,原文:efficiently find parameters' data for different models)而且还是凸函数。 之后我们就可以推导一下GD的公式啦:
向量化写法:
这样最终形式与线性回归是一致的,但是在Logistic回归中,假设htheta是不同的。V2最后,Andrew强调了scaling在logistic回归里同样有效,而且logistic回归在clustering方法里有非常重要应用。
V3介绍了更加牛逼的优化方法。
Conjugate gradient / BFGS /L-BFGS
优点基本是不用手动选取alpha,而且执行效率更高。但算法更加复杂。Andrew的建议反正是不要自己写啦,调库就好。
比如调用matlab库的话就是这样,注意@为指针符号,指向costFunction函数。所以调用快速收敛库的关键就是写对cost function和gradient项。
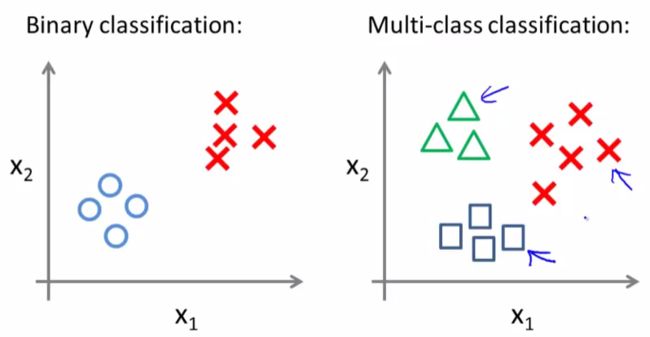
Multiclass Classification
比如邮件自动分类(工作、朋友、家庭……)
那么如何将binary的logistic reg改到multi-class呢?很简答,想分几个组就来几次logistic regression (one-vs-all)。总结如下:
quiz错了一题,大概是几个2类中间有个1类点怎么分,线性假设肯定没有多项式假设好,但是错在GD是可以converge的,我选了不能……囧
Solving the problem of overfitting
Andrew开始介绍overfitting的问题了,并且说采用regularization能够规避此类问题。overfitting大家都很熟悉啦,就是回测吊炸天,预报渣成翔。
那么处理的方法就是1. 手动选取靠谱的feature 2.采用model去选取feature (呵,其实大三统计预报方法已经讲过了逐步回归,不断试错,反复迭代,估计这里思想类似。)
Regularization是个非常牛逼的方法,我们继续保留所有的feature,但是去调节其magnitude,使得一些参数减小。
接下来我们看一下如何实现regularization。直觉上来说,为了使得feature的权重变小,我们可以在cost function中加入关于feature权重的调节项,比如:
这样只有在theta3的平方和theat4的平方足够小时,改版的cost function才能足够小。形象地说,这个过程就是在penalize(惩罚)这两个feature。一般地,我们可以将CF改写成
可以看到最后一项在每一个theta(除了theta0)之前都加入了参数lambda,theta0不考虑在内因为对结果影响不大。最后加入项叫做regularization term(正则化项),lambda称作regularization parameter。
注意lambda的设置如果过大的话,则是对feature的惩戒过大,导致所有theta接近于0,结果近似于h(x)=theta0...这当然是ridiculous的,也就是underfitting
接下来我们试着应用该方法,通过对改进的cost function求导,可以将各个feature update为
注意1-alpha*lambda/m有个神奇的性质,恒小于1.,因此每一轮,thetaj都会被缩小。
如果对NE进行正则化,那么可以得到最终的解析式为(很容易推导):
regularization非常好的一个优点就是能够克服NE不可逆的情况(木有证明,试试看?)。
下面看Logistic Regression的情况,所有的过程都是同LG的,因此可以最终推导出:
梯度下降求导也很简单啦:
然后Andrew就开始开玩笑啦,说我们现在懂的东西呢,就这些线性回归啦,logistic回归啦,什么的,已经比硅谷那些用ML赚了几百万美元的工程师多啦,我去……为啥我只想要那几百万美元呢……不过话说回来,我们可以深入思考一下这个问题:纵向的知识储备确实与实际领域应用的工业产出不一定呈简单的比例关系,或许有一定(可能弱的)正相关。类比例子可以考虑科研产出,这也是前几天和John尬聊职业发展的时候讨论的,John举了个例子说Silicon Valley的企业们呀,比如那个小伙子的FB,为啥就那么成功呢,因为他们抓到了用户痛点(当然John没有用这么商业化的词汇啦,只是说有good idea)然后实现了,科研也是这样,idea is everything。因此知识储备未必是决定赚钱多少的重要feature,事实上idea+足够的实现能力才是,如果idea足够好,商业化的边际成本能压得足够低,是可以触发一系列诸多牛X词汇可以描述的赚钱效应的,比如说盈利的非线性增加(正反馈)/马太效应/黑天鹅效应。不过呢,道理大家都懂,最难的当然是idea啦~
编程作业时发现一个很严重的问题是忘记了X y theta这些矩阵具体是怎么排布的,所以向量化总写不对。
当然还是要100分啦,不过这次真是ddl前半小时才submit的,而且optional没做,不行不行啊……
这部分后面还要回来看一下,尤其是矩阵排布的熟练程度很差。
这两周(我的buffer被我消耗了……)一直在收拾东西准备回程,非常浮躁。toggl也没有利用好,大概总时间在五六个小时吧。