1. 介绍
AVL树又称为高度平衡的二叉搜索树。它能保持二叉树的高度平衡,尽量降低二叉树的高度,减少树的平均搜索长度。
VL树性质:
左子树和右子树的高度之差的绝对值不超过1
树中的每个左子树和右子树都是AVL树
AVL树效率:
一棵AVL树有N个节点,其高度可以保持在lgN,插入/删除/查找的时间复杂度也是lgN。
2. 实现
2.1 类定义
public class AVLTree>{
}
2.2 节点定义
AVL树节点相对于二叉查找树节点,多了一个高度的定义。
高度的定义为:
对于任意结点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0
private static class TreeNode {
T data;
int height;
TreeNode left;
TreeNode right;
public TreeNode(T data) {
this(null, null, data);
}
public TreeNode(TreeNode left, TreeNode right, T data) {
this(left, right, data, 0);
}
public TreeNode(TreeNode left, TreeNode right, T data, int height) {
this.left = left;
this.right = right;
this.data = data;
this.height = height;
}
}
3. 旋转
AVL树最关键的也是最难的一步操作就是旋转。旋转主要是为了实现AVL树在实施了插入和删除操作以后,树重新回到平衡的方法。
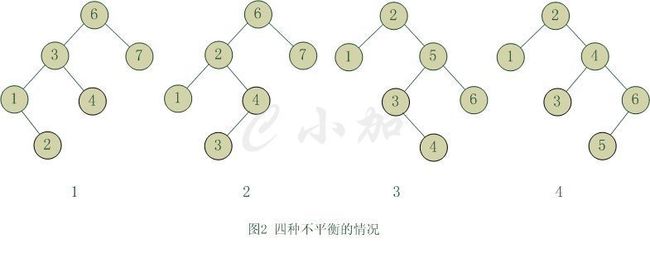
对于一个平衡的节点,由于任意节点最多有两个儿子,因此高度不平衡时,此节点的两颗子树的高度差2.容易看出,这种不平衡出现在下面四种情况:
图一: 6节点的左子树3节点高度比右子树7节点大2,左子树3节点的左子树1节点高度大于右子树4节点,这种情况成为左左。
图二:6节点的左子树2节点高度比右子树7节点大2,左子树2节点的左子树1节点高度小于右子树4节点,这种情况成为左右。
图三:2节点的左子树1节点高度比右子树5节点小2,右子树5节点的左子树3节点高度大于右子树6节点,这种情况成为右左。
图四:2节点的左子树1节点高度比右子树4节点小2,右子树4节点的左子树3节点高度小于右子树6节点,这种情况成为右右。
图一和图四两种情况是对称的,这两种情况的旋转算法是一致的,只需要经过一次旋转就可以达到目标,我们称之为单旋转。
图二和图三两种情况也是对称的,这两种情况的旋转算法也是一致的,需要进行两次旋转,我们称之为双旋转。
3.1 单旋转
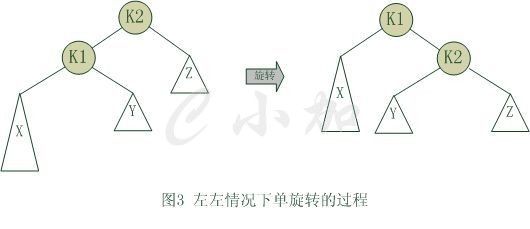
单旋转是针对于左左和右右这两种情况的解决方案,这两种情况是对称的,只要解决了左左这种情况,右右就很好办了。下图是左左情况的解决方案,节点k2不满足平衡特性,因为它的左子树k1比右子树Z深2层,而且k1子树中,更深的一层的是k1的左子树X子树,所以属于左左情况。
为使树恢复平衡,我们把k1变成这棵树的根节点,因为k2大于k1,把k2置于k1的右子树上,而原本在k1右子树的Y大于k1,小于k2,就把Y置于k2的左子树上,这样既满足了二叉查找树的性质,又满足了平衡二叉树的性质。
这样的操作只需要一部分指针改变,结果我们得到另外一颗二叉查找树,它是一棵AVL树,因为X向上一移动了一层,Y还停留在原来的层面上,Z向下移动了一层。整棵树的新高度和之前没有在左子树上插入的高度相同,插入操作使得X高度长高了。因此,由于这颗子树高度没有变化,所以通往根节点的路径就不需要继续旋转了。
/**
* 左左 单旋转
*
* @param node
* @return
*/
private TreeNode leftLeftRotate(TreeNode k2) {
TreeNode k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
k1.height = Math.max(height(k1.left), height(k1.right)) + 1;
return k1;
}
/**
* 右右 单旋转
*
* @param k2
* @return
*/
private TreeNode rightRightRotate(TreeNode k2) {
TreeNode k1 = k2.right;
k2.right = k1.left;
k1.left = k2;
k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
k1.height = Math.max(height(k1.left), height(k1.right)) + 1;
return k1;
}
3.2 双旋转
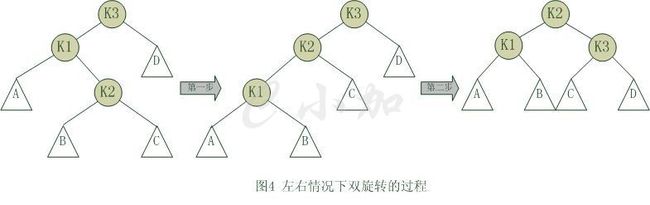
对于左右和右左这两种情况,单旋转不能使它达到一个平衡状态,要经过两次旋转。双旋转是针对于这两种情况的解决方案,同样的,这样两种情况也是对称的,只要解决了左右这种情况,右左就很好办了。下图是左右情况的解决方案,节点k3不满足平衡特性,因为它的左子树k1比右子树D深2层,而且k1子树中,更深的一层的是k1的右子树k2子树,所以属于左右情况。
为使树恢复平衡,我们需要进行两步,第一步,把k1作为根,进行一次右右旋转,旋转之后就变成了左左情况,所以第二步再进行一次左左旋转,最后得到了一棵以k2为根的平衡二叉树。
/**
* LR:双旋转-----先RR后LL
*
* @param k3
* @return
*/
public TreeNode leftRightRotate(TreeNode k3) {
k3.left = rightRightRotate(k3.left);
return leftLeftRotate(k3);
}
/**
* 双旋转-----先LL后RR
*
* @param k1
* @return
*/
public TreeNode rightLeftRotate(TreeNode k1) {
k1.left = leftLeftRotate(k1.left);
return rightRightRotate(k1);
}
4. 主要方法
AVL树 的 T max() 、T min()、TreeNode 与 二叉查找树 的逻辑完全一样。只是写法可以分为 递归写法 与 非递归写法。本文采用 非递归写法。
4.1 最大值 T max()
public T max() {
if(root == null) {
return null;
}
TreeNode node = root;
while (node.right != null) {
node = node.right;
}
return node.data;
}
4.1 最小值 T min()
public T min() {
if(root == null) {
return null;
}
TreeNode node = root;
while (node.left != null) {
node = node.left;
}
return node.data;
}
4.2 搜索 TreeNode search(T data)
public TreeNode search(T data) {
TreeNode node = root;
while (node != null) {
int result = node.data.compareTo(data);
if (result == 0) {
return node;
}
node = result > 0 ? node.left : node.right;
}
return node;
}
4.3 插入 void insert(T data)
public void insert(T data) {
if (data == null) {
throw new IllegalArgumentException("The data can't be null");
}
root = insert(data, root);
}
private TreeNode insert(T data, TreeNode node) {
if (node == null) {
node = new TreeNode(data);
return node;
}
int result = node.data.compareTo(data);
if (result == 0) {
throw new IllegalArgumentException("the AVL Tree can't have the same data for:" + data);
}
if (result > 0) {
node = insert(data, node.left);
if (height(node.left) - height(node.right) >= 2) {
if (data.compareTo(node.left.data) < 0) {
node = leftLeftRotate(node);
} else {
node = leftRightRotate(node);
}
}
} else {
node = insert(data, node.right);
if (height(node.right) - height(node.left) >= 2) {
if (data.compareTo(node.right.data) < 0) {
node = rightRightRotate(node);
} else {
node = rightLeftRotate(node);
}
}
}
node.height = Math.max(height(node.left), height(node.right)) + 1;
return node;
}
4.4 删除 void remove(T data)
删除逻辑与 二叉查找树 的逻辑完全一样,仅仅多了旋转的逻辑。
public void remove(T data) {
if (data == null) {
throw new IllegalArgumentException("The data can't be null");
}
root = remove(data, root);
}
private TreeNode remove(T data, TreeNode node) {
if (node == null) {
return null;
}
int result = node.data.compareTo(data); // 判断 节点值 和 要删除的节点值的大小
if (result > 0) { // 如果大于 0,则表示需要删除的节点在此节点的左边,删除后,此节点的右子树将高于左子树。
node.left = remove(data, node.left);
if (height(node.right) - height(node.left) >= 2) { // 如果右子树高度 - 左子树高度 大于等于 2, 则表明需要进行旋转。且旋转肯定是 右右 和 右左之一
TreeNode temp = node.right;
if (temp != null) {
if (height(temp.right) > height(temp.left)) {
node = rightRightRotate(node);
} else {
node = rightLeftRotate(node);
}
}
}
} else if (result < 0) { // 如果小于 0,则表示需要删除的节点在此节点的边,删除后,此节点的左子树将高于右子树。
node.right = remove(data, node.right);
if (height(node.left) - height(node.right) >= 2) { // 如果左子树高度 - 右子树高度 大于等于 2, 则表明需要进行旋转。且旋转肯定是 左左 和 左右之一
TreeNode temp = node.left;
if (temp != null) {
if (height(temp.left) > height(temp.right)) {
node = leftLeftRotate(node);
} else {
node = leftRightRotate(node);
}
}
}
} else { // 如果相等,则表示此节点就是需要删除的节点,删除方式与二叉查找树的删除方式一样
if (node.left != null && node.right != null) {
TreeNode minRight = min(node.right);
node.data = minRight.data;
node.right = remove(minRight.data, node.right);
} else if (node.left == null && node.right == null) {
node = null;
} else if (node.left == null || node.right == null) {
node = (node.left != null) ? node.left : node.right;
}
}
if (node != null) {
node.height = Math.max(height(node.left), height(node.right)) + 1;
}
return node;
}