1 简单排序算法
1.1 冒泡排序
sort algorithms_bubble.jpg
排序原理
比较相邻两数据，如果数据反序，则交换两数据的位置；指针后移，继续比较，直到未排序队列尾部。每一趟将待排序队列最大或最小数据冒泡至待排序队列尾部。最终达到完全有序。
代码实现
/**
* 冒泡排序
*/
public static void bubbleSort(int[] array) {
for (int i = array.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (array[j] > array[j + 1]) {
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
}
算法效率
每一轮比较将有一项数据排好序，因此下一轮比较次数将减一
比较次数= (N-1) + (N-2) + ... + 2 + 1 = N(N-1)/2 即 O(N²)
大约有一半次数会进行数据交换
交换次数=((N-1) + (N-2) + ... + 2 + 1)/2 = N(N-1)/4 即 O(N²)
时间复杂度:O(N²)
1.2 选择排序
sort algorithms_selection.jpg
排序原理
每次遍历从无序队列中选择最小数据将其放至无序队列队首。
代码实现
/**
* 选择排序
*/
public static void selectionSort(int[] array) {
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i + 1; j < array.length; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
if(minIndex != i){
int temp = array[i];
array[i] = array[minIndex];
array[minIndex] = temp;
}
}
}
算法效率
选择排序与冒泡排序执行了相同次数的比较
比较次数= (N-1) + (N-2) + ... + 2 + 1 = N(N-1)/2 即 O(N²)
但是交换次数减少至O(N)
交换次数= N 即 O(N)
时间复杂度:O(N²)
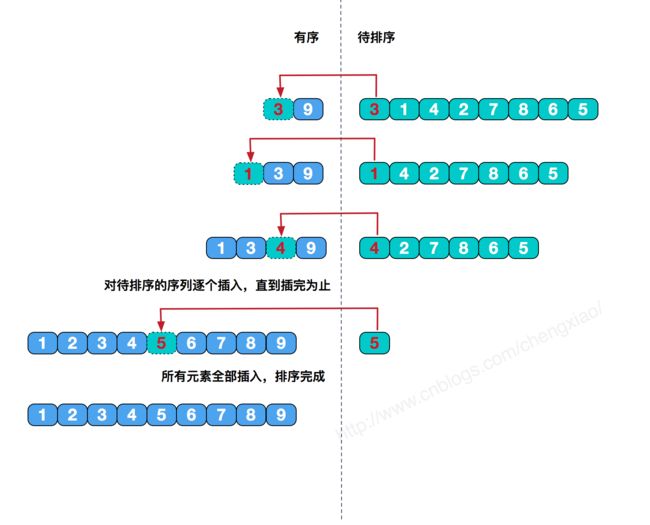
1.3 插入排序
sort algorithms_insert.jpg
排序原理
插入排序在遍历时，遍历数据左边已经有序，将当前数据插入左边有序队列中适当位置；遍历完成时，整个队列有序。
代码实现
/**
* 插入排序
*/
public static void insertSort(int[] array) {
int value;
for (int i = 1; i < array.length; i++) {
value = array[i];
int j = i;
while (j > 0 && array[j - 1] > value) {
array[j] = array[j - 1];
j--;
}
array[j] = value;
}
}
算法效率
平均比较次数约为总的一半
比较次数= (1 + 2 + ... + (N-2) + (N-1))/2 = N(N-1)/4 即 O(N²)
复制与交换耗时不同，复制耗时更少；复制次数约等同于比较次数
复制次数= N(N-1)/4 即 O(N²)
时间复杂度:O(N²)
总结
相对于随机数据,插入排序速度比冒泡排序快一倍，比选择排序略快。
2 复杂排序算法
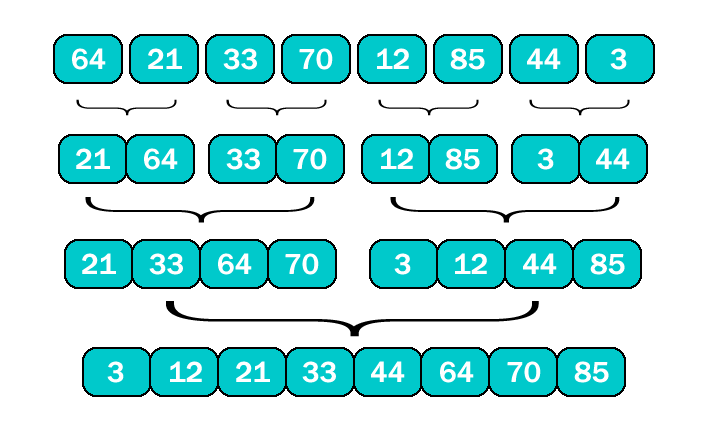
2.1 归并排序
sort algorithms_merge.png
排序原理
归并排序算法将数据分为两组，分别对每组数据排序，然后使用归并算法，归并两个有序数组。对每个分组的排序则又可以使用归并排序算法排序。
代码实现
public class MergeSort {
/**
* 归并排序算法
*/
public static void mergeSort(int[] sourceArray) {
int[] tempArray = new int[sourceArray.length];
mergeSort(sourceArray, tempArray, 0, sourceArray.length - 1);
}
private static void mergeSort(int[] sourceArray, int[] tempArray, int fromIndex, int lastIndex) {
if (fromIndex == lastIndex) {
return;
} else {
int midIndex = (fromIndex + lastIndex) / 2;
/* 对两个子分组使用归并排序 */
mergeSort(sourceArray, tempArray, fromIndex, midIndex);
mergeSort(sourceArray, tempArray, midIndex + 1, lastIndex);
/* 使用归并算法将两个有序子分组归并为一个有序数组 */
merge(sourceArray, tempArray, fromIndex, midIndex, midIndex + 1, lastIndex);
}
}
private static void merge(int[] sourceArray, int[] tempArray, int firstFromIndex, int firstLastIndex,
int secondFromIndex, int secondLastIndex) {
int firstCountIndex = firstFromIndex;
int secondCountIndex = secondFromIndex;
int tempArrayIndex = 0;
while (firstCountIndex <= firstLastIndex && secondCountIndex <= secondLastIndex) {
if (sourceArray[firstCountIndex] < sourceArray[secondCountIndex]) {
tempArray[tempArrayIndex++] = sourceArray[firstCountIndex++];
} else if (sourceArray[firstCountIndex] > sourceArray[secondCountIndex]) {
tempArray[tempArrayIndex++] = sourceArray[secondCountIndex++];
} else {
tempArray[tempArrayIndex++] = sourceArray[firstCountIndex++];
tempArray[tempArrayIndex++] = sourceArray[secondCountIndex++];
}
}
while (firstCountIndex <= firstLastIndex) {
tempArray[tempArrayIndex++] = sourceArray[firstCountIndex++];
}
while (secondCountIndex <= secondLastIndex) {
tempArray[tempArrayIndex++] = sourceArray[secondCountIndex++];
}
for (int i = 0; i < tempArrayIndex; i++) {
sourceArray[firstFromIndex + i] = tempArray[i];
}
}
}
算法效率
时间复杂度:O(NlogN)
缺点
需要一个和待排序数组一样大小的临时存储空间。
2.2 希尔排序
排序原理
希尔排序又命增量排序。希尔排序通过加大插入排序中元素之间的间隔，并在这些有间隔的元素中进行插入排序，从而使数据项能大跨度的移动。当这些数据项排过一次序后，希尔排序算法减小数据项的间隔（即增量，通常用h表示）再进行排序，依此进行下去，最后使用1-增量排序后，算法结束。
代码实现
public class ShellSort {
public static void shellSort(int[] array) {
int h = 1;
/* 计算初始增量h */
while ((3 * h + 1) <= array.length) {
h = 3 * h + 1;
}
int temp;
/* 增量为0，排序结束 */
while (h > 0) {
/* 进行h-增量排序 */
for (int i = h; i < array.length; i++) {
temp = array[i];
int j = i;
while (j > h - 1 && array[j - h] > temp) {
array[j] = array[j - h];
j -= h;
}
array[j] = temp;
}
/* 减少增量h */
h = (h - 1) / 3;
}
}
}
2.3 快速排序
排序原理
根据枢纽值，采用划分算法，将数组分为左右两个子数组，然后采用递归方式，分别对左右两个子数组进行排序。
代码实现
public class QuickSort {
public static void quickSort(int[] array) {
quick(array, 0, array.length - 1);
}
private static void quick(int[] array, int left, int right) {
if (right <= left) {
return;
} else {
/* 计算划分算法枢纽值 */
int pivot = (array[left] + array[right] + array[(left + right) / 2]) / 3;
/* 划分算法划分数组，返回枢纽值位置 */
int parttion = partition(array, left, right, pivot);
/* 排序枢纽值左边的子数组（递归调用快排） */
quick(array, left, parttion);
/* 排序枢纽值又边的子数组（递归调用快排） */
quick(array, parttion + 1, right);
}
}
private static int partition(int[] array, int leftIndex, int rightIndex, int pivot) {
while (true) {
while (leftIndex < rightIndex && array[leftIndex] < pivot) {
leftIndex++;
}
while (rightIndex > leftIndex && array[rightIndex] > pivot) {
rightIndex--;
}
if (leftIndex >= rightIndex) {
break;
} else {
int temp = array[leftIndex];
array[leftIndex] = array[rightIndex];
array[rightIndex] = temp;
}
}
return array[leftIndex] > pivot ? leftIndex - 1 : leftIndex;
}
}
算法效率
时间复杂度:O(NlogN)
2.4 堆排序
2.4.1 什么是堆
堆的特性
①堆是完全二叉树，除了树的最后一层节点不需要是满的，其它每一层从左到又都完全是满的。
②堆中每一个节点关键字都大于（或等于）这个节点的子节点的关键字。
③堆常常使用数组实现(由于是完全二叉树，数组不存在“空洞”)。
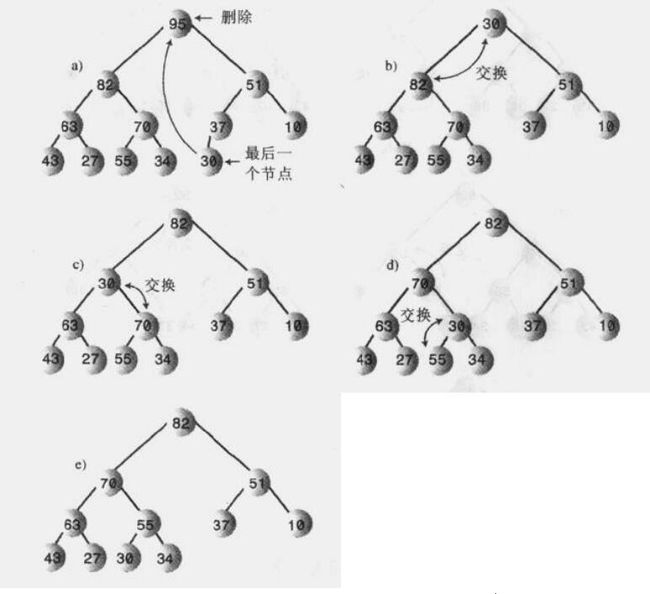
移除remove
移除是指删除关键字最大的节点，这个节点总是根节点，其在数组中的索引为0。
一旦移除根节点，数组出现“空洞”(即数组索引为0的位置)，树不再是完全二叉树，因此需要填补，使其重新成为完全二叉树。步骤如下：
①移除根。
②将最后一个节点(即数组中最后一个节点)移到根的位置。
③向下筛选这个节点，直到它处于一个大于它的节点之下，小于它的节点之上。
注意：筛选过程中，该节点需与较大子节点进行交换。否则将使较小子节点成为较大子节点的父节点。
sort algorithms_heapArray_remove.jpg
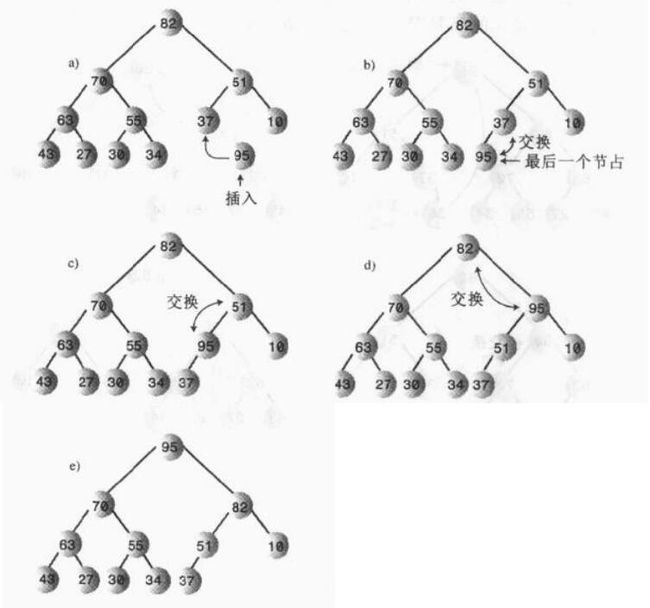
插入insert
插入采用向上筛选方式：
①将节点插入堆的最后，即数组的最后。
②与父节点比较，如果大于父节点则互换位置，直至节点出于一个大于它的父节点之下或成为根节点。
sort algorithms_heapArray_insert.jpg
基于数组的堆的代码实现
在数组中，如果一个节点的索引为x，则
父节点索引为(x-1)/2
左子节点索引为2x+1
右子节点索引为2x+2
public class Heap {
private int[] heapArray;
private int count;
public Heap(int[] heapArray, int count) {
this.heapArray = heapArray;
this.count = count;
}
public void insert(int num) {
heapArray[count] = num;
trickleUp(count++);
}
public int remove() {
int returnVal = heapArray[0];
heapArray[0] = heapArray[--count];
trickleDown(0);
return returnVal;
}
/**
* 向上筛选
*/
public void trickleUp(int index) {
int parent = (index - 1) / 2;
int indexVal = heapArray[index];
while (index > 0 && heapArray[parent] < indexVal) {
heapArray[index] = heapArray[parent];
index = parent;
parent = (index - 1) / 2;
}
heapArray[index] = indexVal;
}
/**
* 向下筛选
*/
public void trickleDown(int index) {
int largerChildIndex;
int indexVal = heapArray[index];
int leftChildIndex = 2 * index + 1;
int rightChildIndex = leftChildIndex + 1;
while (leftChildIndex < count) {
if (rightChildIndex < count && heapArray[rightChildIndex] > heapArray[leftChildIndex]) {
largerChildIndex = rightChildIndex;
} else {
largerChildIndex = leftChildIndex;
}
if (indexVal > heapArray[largerChildIndex]) {
break;
} else {
heapArray[index] = heapArray[largerChildIndex];
index = largerChildIndex;
leftChildIndex = 2 * index + 1;
rightChildIndex = leftChildIndex + 1;
}
}
heapArray[index] = indexVal;
}
}
2.4.2 堆排序
排序原理
利用堆的特性，调用insert方法，将待排序数组插入堆中，再调用remove方法，将数据取出，即完成排序。
代码实现
public class HeapSort {
public static void heapSort(int[] array) {
Heap heap = new Heap(new int[array.length], 0);
for (int i = 0; i < array.length; i++) {
heap.insert(array[i]);
}
for (int j = array.length - 1; j >= 0; j--) {
array[j] = heap.remove();
}
}
}
缺点：这种方式需要额外一个数组生成一个和待排序数组一样大小的临时空间。
将待排序数组看做是一个堆的数组表示，堆所有非叶子节点使用向下筛选
trickleDown方法,筛选完成，则数组变成一个正确的堆数组。然后再调用remove方法将数据移除；由于移除一个数据后，数组将空出一位，将移除数据，存入空出的空间即可。代码实现
public class HeapSort {
public static void heapSort(int[] array) {
Heap heap = new Heap(array, array.length);
for (int i = array.length / 2 - 1; i >= 0; i--) {
heap.trickleDown(i);
}
for (int j = array.length - 1; j >= 0; j--) {
array[j] = heap.remove();
}
}
}
算法效率
因为insert和remove方法的时间复杂度都是O(logN),而每个方法需要执行N此，因此
堆排序时间复杂度为O(NlogN)
由于其while循环中执行操作要比快速排序复杂，其排序速度不如快速排序。
优点：节省时间、节省内存。