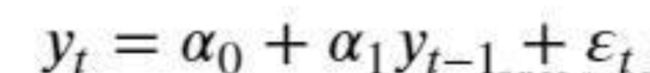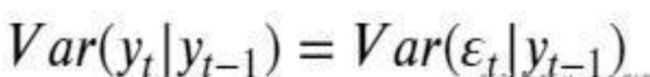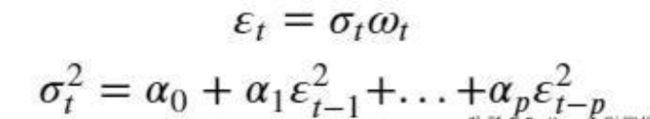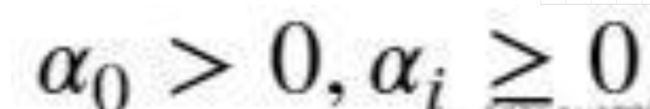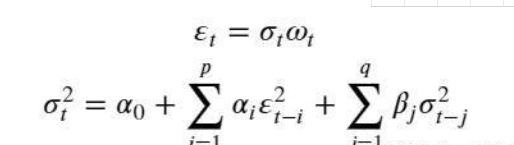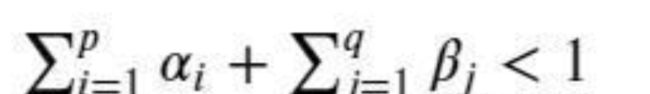Python玩转金融时间序列之ARCH与GARCH模型

01 引言

作为金融时间序列的专题推文，【手把手教你】时间序列之日期处理主要介绍了使用Python处理时间序列的日期和统计分析；【Python量化基础】时间序列的自相关性与平稳性主要介绍了时间序列的一些基础概念，包括自相关性、偏自相关性、白噪声和平稳性；而【手把手教你】使用Python玩转金融时间序列模型主要介绍了AR、MA、ARMA和ARIMA模型的基本原理与Python的实现。从上一篇推文不难看出，使用ARMA等模型对股票收益率的时间序列建模效果不是很理想，主要在于忽略了时间序列的异方差和波动聚集特性。所谓波动性聚集，是指金融时间序列的波动具有大波动接着大波动，小波动接着小波动的特征，即波峰和波谷具有连续性。ARCH和GARCH模型正是基于条件异方差和波动聚集的特性建模的。本次推文着重介绍 ARCH和GARCH模型的基本原理及其Python实现。

02 股票收益率时间序列特点

在介绍ARCH和GARCH模型之前，我们先来看看金融资产收益率的时间序列有哪些比较突出的特点。仍然以沪深300指数为例，考察其收益率时间的分布和统计特性。下面的Python代码与上一篇推文类似，包括导入需要用到的库、定义画图函数和使用tushare获取数据等。遇到问题没人解答，小编创建了一个Python学习交流裙：五二八 三九七 六一七， 寻找有志同道合的小伙伴，互帮互助，群里还有不错的学习视频教程和PDF电子书分享！

import pandas as pd

import numpy as np

import statsmodels.tsa.api as smt

#tsa为Time Series analysis缩写

import statsmodels.api as sm

import scipy.stats as scs

from arch import arch_model

#画图

import matplotlib.pyplot as plt

import matplotlib as mpl

%matplotlib inline

#正常显示画图时出现的中文和负号

from pylab import mpl

mpl.rcParams['font.sans-serif']=['SimHei']

mpl.rcParams['axes.unicode_minus']=False

def ts_plot(data, lags=None,title=''):

if not isinstance(data, pd.Series):

data = pd.Series(data)

#matplotlib官方提供了五种不同的图形风格，

#包括bmh、ggplot、dark_background、

#fivethirtyeight和grayscale

with plt.style.context('ggplot'):

fig = plt.figure(figsize=(10, 8))

layout = (3, 2)

ts_ax = plt.subplot2grid(layout, (0, 0))

acf_ax = plt.subplot2grid(layout, (1, 0))

pacf_ax = plt.subplot2grid(layout, (1, 1))

qq_ax = plt.subplot2grid(layout, (2, 0))

pp_ax = plt.subplot2grid(layout, (2, 1))

data.plot(ax=ts_ax)

ts_ax.set_title(title+'时序图')

smt.graphics.plot_acf(data, lags=lags,

ax=acf_ax, alpha=0.5)

acf_ax.set_title('自相关系数')

smt.graphics.plot_pacf(data, lags=lags,

ax=pacf_ax, alpha=0.5)

pacf_ax.set_title('偏自相关系数')

sm.qqplot(data, line='s', ax=qq_ax)

qq_ax.set_title('QQ 图')

scs.probplot(data, sparams=(data.mean(),

data.std()), plot=pp_ax)

pp_ax.set_title('PP 图')

plt.tight_layout()

return

使用tushare获取沪深300交易数据

import tushare as ts

token='输入你的token'

pro=ts.pro_api(token)

df=pro.index_daily(ts_code='000300.SH')

df.index=pd.to_datetime(df.trade_date)

del df.index.name

df=df.sort_index()

df['ret']=np.log(df.close/df.close.shift(1))

#df.head()

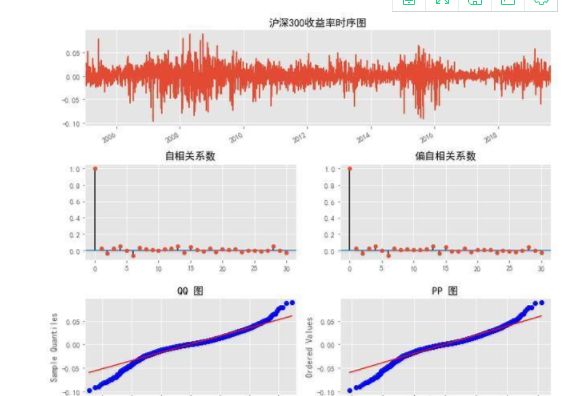
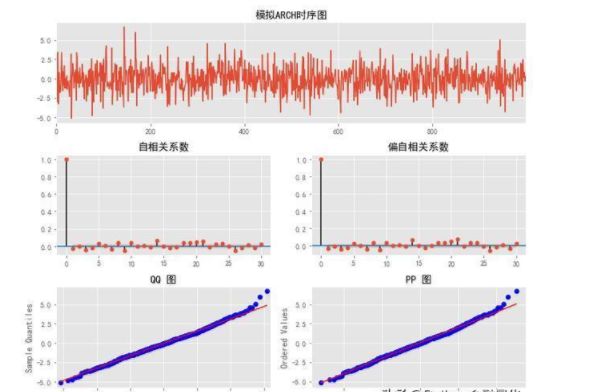
ts_plot(df.ret.dropna(),lags=30,title='沪深300收益率')

从上图可以看出，沪深300指数收益率时间序列呈现出以下几个现象，具有一定的普遍性。

自相关性比较弱，但对其进行变换后，如取平方、绝对值等，则表现出很强的自相关性（见后文）；

收益率的条件方差（Conditional Variance）随着时间而变化，即存在条件异方差的特征。

收益率序列的波动具有持续性，即存在波动集聚（Volatility Clustering）的现象。比如2007-2008、2015-2016、2019具有较大的波动性。

QQ图显示，收益率并不服从正态分布，极端值较多，具有厚尾的现象。

03 ARCH模型

ARCH模型全称是自回归条件异方差模型，Autoregressive Conditionally Heteroskedastic Models - ARCH(p)，是Engle在1982年分析英国通货膨胀率时提出的模型，主要用于刻画波动率的统计特征。

一般先假设收益率序列满足某个经典时间序列模型（MA、AR或ARMA），以AR（1）模型为例：

收益率yt的波动率（条件方差）可以使用残差项的波动率进行刻画：

为了刻画资产收益率的这种波动特性，可以令残差项的条件方差与过去残差项的平方相关。因此，ARCH（p）模型可以表示为：

其中，w是均值为0，方差为1的独立同分布时间序列，

，且满足一定条件使得的无条件方差有限。ARCH(p)模型能够很好地刻画金融资产收益率序列的波动特性和厚尾现象，但是其本身并不能用来解释金融资产收益率为何有这样的特征。关于ARCH模型的估计此处不详细展开，感兴趣的可以参见Ruey S. Tray的《金融时间序列分析》和计量经济学教材。下面简要介绍ARCH模型的建模步骤：

（1）检验收益率序列是否平稳，根据自相关性建立合适的均值方程，如ARMA模型，描述收益率如何随时间变化，根据拟合的模型和实际值，得到残差序列。

（2）对拟合的均值方程得到的残差序列进行ARCH效应检验，即检验收益率围绕均值的偏差是否时大时小。检验序列是否具有ARCH效应的方法有两种：Ljung-Box检验和LM检验。

（3）若ARCH效应在统计上显著，则需要再设定一个波动率模型来刻画波动率的动态变化。

（4）对均值方差和波动率方差进行联合估计，即假设实际数据服从前面设定的均值方差和波动率方差后，对均值方差和波动率方差中的参数进行估计，并得到估计的误差。

（5）对拟合的模型进行检验。如果估计结果（残差项）不满足模型本身的假设，则模型的可用性较差。

下面使用Python模拟ARCH模型并对沪深300收益率的ARCH效应进行统计检验。

# 模拟ARCH时间序列

np.random.seed(2)

a0 = 2

a1 = .5

y = w = np.random.normal(size=1000)

Y = np.empty_like(y)

for t in range(1,len(y)):

Y[t] = w[t] * np.sqrt((a0 + a1*y[t-1]**2))

ts_plot(Y, lags=30,title='模拟ARCH')

def ret_plot(ts, title=''):

ts1=ts**2

ts2=np.abs(ts)

with plt.style.context('ggplot'):

fig = plt.figure(figsize=(12, 6))

layout = (2, 1)

ts1_ax = plt.subplot2grid(layout, (0, 0), colspan=2)

ts2_ax = plt.subplot2grid(layout, (1, 0))

ts1.plot(ax=ts1_ax)

ts1_ax.set_title(title+'日收益率平方')

ts2.plot(ax=ts2_ax)

ts2_ax.set_title(title+'日收益率绝对值')

plt.tight_layout()

return

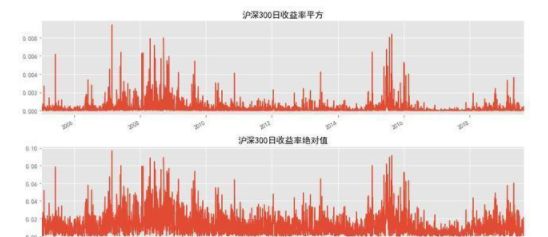
ret_plot(df.ret.dropna(), title='沪深300')

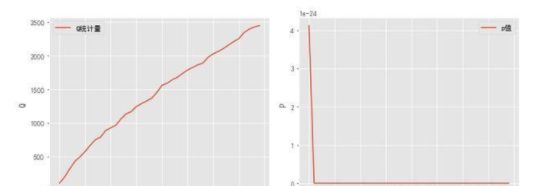
从沪深300的日收益平方和绝对值走势图可以看出，存在较明显的波动聚集的现象，初步可以判断出沪深300日收益序列存在ARCH效应。下面使用Ljung-Box统计量对收益率平方的自相关性进行统计检验。计算Q统计量和LB统计量都是用python中statsmodels模块acorr_ljungbox方法. 默认情况下, acorr_ljungbox只计算LB统计量, 只有当参数boxpierce=True时, 才会输出Q统计量。由LB白噪声检验可以看出，Q统计量的p值都在0.05以下, 表明原假设成立的概率极小, 可以拒绝沪深300收益率的平方是白噪音序列的原假设，说明原序列（沪深300收益率）存在ARCH效应。

def whitenoise_test(ts):

'''计算box pierce 和 box ljung统计量'''

from statsmodels.stats.diagnostic import acorr_ljungbox

q,p=acorr_ljungbox(ts)

with plt.style.context('ggplot'):

fig = plt.figure(figsize=(10, 4))

axes = fig.subplots(1,2)

axes[0].plot(q, label='Q统计量')

axes[0].set_ylabel('Q')

axes[1].plot(p, label='p值')

axes[1].set_ylabel('P')

axes[0].legend()

axes[1].legend()

plt.tight_layout()

return

ret=df.ret.dropna()

whitenoise_test(ret**2)

04 GARCH模型

GARCH模型是Bollerslev在1986年提出来的，全称为广义自回归条件异方差模型，Generalized Autoregressive Conditionally Heteroskedastic Models - GARCH(p,q)，是ARCH模型的扩展。GARCH模型认为时间序列每个时间点变量的波动率是最近p个时间点残差平方的线性组合，与最近q个时间点变量波动率的线性组合加起来得到。即GARCH模型的条件方差不仅是滞后残差平方的线性函数，还是滞后条件方差的线性函数，因而GARCH模型适合在计算量不大时，方便地描述高阶的ARCH过程，具有更大的适用性。

其中，

为白噪音，

，否则模型将是非平稳的。GARCH模型的估计与ARCH模型类似，具体推导过程参见计量经济学相关书籍。在实际应用中，GARCH(1,1)和GARCH(2,1)一般可以满足对自回归条件异方差的描述。下面使用Python对GARCH(1,1)模型进行模拟和估计。

Python中的ARCH包

先来看下arch包中arch_model函数各参数的含义以及模型设定方法。

arch.arch_model(y, x=None, mean='Constant', lags=0, vol='Garch', p=1, o=0, q=1, power=2.0, dist='Normal', hold_back=None)

各参数含义:

y : 因变量。

x : 外生变量，如果没有外生变量则模型自动省略。

mean: 均值模型的名称，可选: ‘Constant’, ‘Zero’, ‘ARX’ 以及 ‘HARX’。

lags:滞后阶数。

vol :波动率模型，可选: ‘GARCH’ （默认）, ‘ARCH’, ‘EGARCH’, ‘FIARCH’ 以及 ‘HARCH’。

p :– 对称随机数的滞后阶,即扣除均值后的部分。

o ：非对称数据的滞后阶。

q ：波动率或对应变量的滞后阶。

power：使用GARCH或相关模型的精度。

dist：误差分布，可选：正态分布: ‘normal’, ‘gaussian’ (default)；学生T分布: ‘t’, ‘studentst’；偏态学生T分布: ‘skewstudent’, ‘skewt’；通用误差分布: ‘ged’, ‘generalized error”。

hold_back：对同一样本使用不同的滞后阶来比较模型时使用该参数。

# 模拟GARCH(1, 1) 过程

np.random.seed(1)

a0 = 0.2

a1 = 0.5

b1 = 0.3

n = 10000

w = np.random.normal(size=n)

garch = np.zeros_like(w)

sigsq = np.zeros_like(w)

for i in range(1, n):

sigsq[i] = a0 + a1*(garch[i-1]**2) + b1*sigsq[i-1]

garch[i] = w[i] * np.sqrt(sigsq[i])

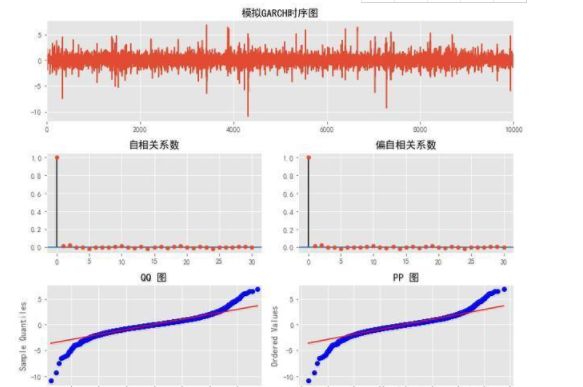
_ = ts_plot(garch, lags=30,title='模拟GARCH')

#update_freq=0表示不输出中间结果，只输出最终结果

# 使用模拟的数据进行 GARCH(1, 1) 模型拟合

#arch_model默认建立GARCH（1,1）模型

am = arch_model(garch)

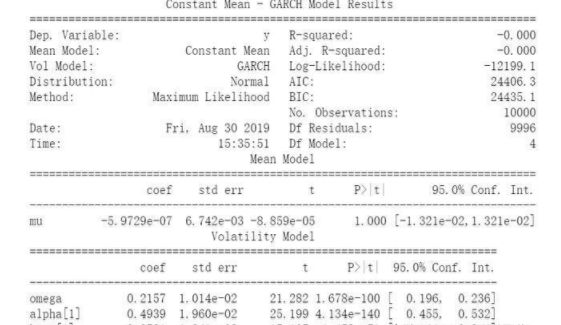
res = am.fit(update_freq=0)

print(res.summary())

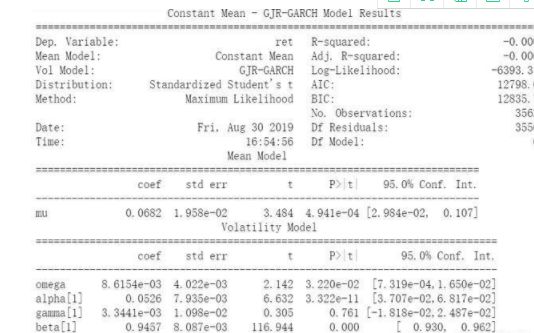
#拟合沪深300收益率数据

Y=ret*100.0

am = arch_model(Y,p=1, o=1, q=1, dist='StudentsT')

res = am.fit(update_freq=0)

#update_freq=0表示不输出中间结果，只输出最终结果

print(res.summary())

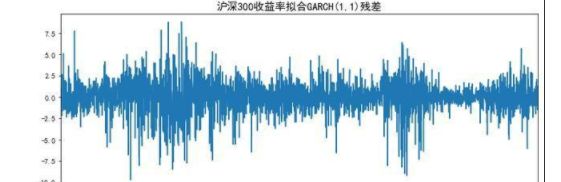
res.resid.plot(figsize=(12,5))

plt.title('沪深300收益率拟合GARCH(1,1)残差',size=15)

plt.show()

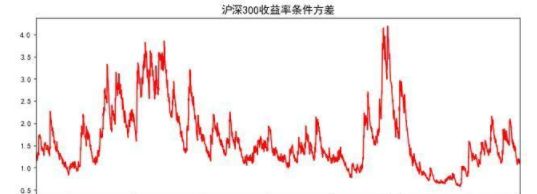
res.conditional_volatility.plot(figsize=(12,5),color='r')

plt.title('沪深300收益率条件方差',size=15)

plt.show()

05 结语

本文简要介绍了ARCH和GARCH模型的基本原理和Python实现，关于其应用还有待进一步拓展和挖掘。ARCH和GARCH模型能够较好的刻画金融资产收益率的波动性聚集和厚尾现象，因此在量化投资上的应用主要表现在波动率的估计上，尤其是金融工程（期权波动率）和风险管理（VaR模型）的应用上。同时，我们也注意到，ARCH和GARCH模型在应用中也存在一定的局限性和不足：首先，模型假定波动是对称的，即过去的波动对现在条件方差的影响是相同的，但学术上的实证结果却表明，当坏（好）消息发布时，股票收益率的波动会增加（减小）；其次，模型对参数的限制条件较强，尤其是高阶模型，参数需要满足的约束非常复杂。最后，模型并没有提供关于波动率变化的更进一步解释，而仅仅是拟合波动率变化的统计行为。针对现有模型的不足，学者们在GARCH模型的基础上又提出了一系列模型，简称GARCH模型族，包括IGARCH、TGARCH、EGARCH等，更复杂的还有BEKK-GARCH、Coupla-GARCH等模型。当然，模型并非越复杂越好，特别地，学术上用到的复杂模型，在现实的量化投资中能用到的往往很少。