数据结构算法（五） 之 树的 2 道面试题 23 & 24

• 剑指 Offer 面试题 23（Java 版）：从上往下打印二叉树

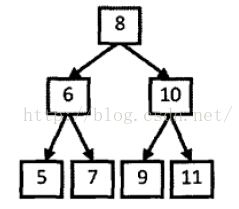
题目：从上往下打印二叉树的每个结点，同一层的结点按照从左到右的顺序打印。例如输入下图的二叉树，则一次打印出8，6，10，5，7，9，11。

例子

因为按层打印的顺序决定应该先打印的根结点，所以我们从树的根结点开始分析。为了接下来能够打印 8 的结点的两个子结点，我们应该在遍历到该结点时把值为 6 和 10 的两个结点保存到一个容器中，现在容器内就有两个结点了。按照从左到右打印的要求，我们先取出值为 6 的结点。打印出 6 后把它的值分别为 5 和 7 的两个结点放入数据容器。此时数据容器中有三个结点，值分别为10，5，7。接下来我们从数据容器中取出值为 10 的结点。注意到值为 10 的结点比值为 5，7 的结点先放入容器，此时又比这两个结点先取出，这就是我们通常说的先入先出，因此不难看出这个容器应该是一个队列。由于值为5，7，9，11 的结点都没有子结点，因此只要依次打印即可。

思路：通过分析具体例子，我们可以找到从上到下打印二叉树的规律：每一次打印一个结点的时候，如果该结点有子结点，把该结点的子结点放到一个队列的尾。接下来到队列的头部取出最早进入队列的结点，重复前面打印操作，直到队列中所有的结点都被打印出为止。

show my code

/**
 * 层序打印二叉树
 * @author innovator
 *
 */
public class PrintTreeByFloor {
    
    /**
     * 层序遍历树
     * @param root
     */
    public static void printTreeByFromTop2Bottom(BinaryTreeNode root){
        
        if(root == null){
            return;
        }
        
        //用队列装每次遍历到的结点
        Queue queue = new LinkedList();
        //存放头结点
        queue.add(root);
        
        while(queue.size() >0){
            //出队
            BinaryTreeNode temp = queue.poll();
            System.out.println("结点的值："+temp.value);
            
            //左子结点不为空，则放进队列
            if(temp.leftNode != null){
                queue.add(temp.leftNode);
            }
            
            if(temp.rightNode != null){
                queue.add(temp.rightNode);
            }
        }
    }
    
    
    public static void main(String[] args){  
        BinaryTreeNode A = new BinaryTreeNode(8);  
        BinaryTreeNode B = new BinaryTreeNode(6); 
        BinaryTreeNode C = new BinaryTreeNode(10);
        BinaryTreeNode D = new BinaryTreeNode(5);
        BinaryTreeNode E = new BinaryTreeNode(7);
        BinaryTreeNode F = new BinaryTreeNode(9);
        BinaryTreeNode G = new BinaryTreeNode(11);
    
        A.leftNode = B;  
        A.rightNode = C;
        B.leftNode = D;  
        B.rightNode = E;
        C.leftNode = F;  
        C.rightNode = G;

        printTreeByFromTop2Bottom(A);
    }

}

结果

• 剑指 Offer 面试题 24（Java 版）：二叉搜索树的后序遍历序列

题目：输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true，否则返回false。假设输入的数组的任意两个数字都互不相同。

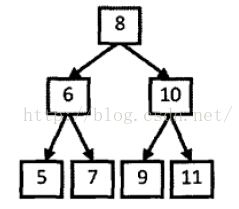
例如输入数组｛5，7，6，9，11，10，8｝则返回true，因为这个整数序列是下图二叉树的后序遍历的结果。如果输入的数组是｛7，4，6，5｝，由于没有哪颗二叉搜索树的后续遍历的结果是这个序列，因此返回false。

例子

思路：在后序遍历得到的序列中，最后一个数字是树的根结点的值。数组中前面的数字可以分为两部分：第一部分是左子树结点的值，它们都比根结点的值小；第二部分是右子树结点的值，他们都比根结点的值大。

以数组｛5，7，6，9，11，10，8｝为例，后序遍历结果的最后一个数字 8 就是根结点的值。在这个数组中，前 3 个数字 5，7 和 6
都比 8 小，是值为 8 的结点的左子树结点；后 3 个数字 9，11 和
10 都比 8 大，是值为 8 的结点的右子树结点。

我们接下来用同样的方法确定与数组每一部分对应的子树的结构。这其实就是一个递归的过程。对于序列 5，7，6，最后一个数字 6是左子树的根结点的值。数字 5 比 6 小，是值为 6 的结点的左子结点，而 7 则是它的右子结点。同样，在序列 9，11，10 中，最后一个数字 10 是右子树的根结点，数字 9 比 10 小，是值为 10 的结点的左子结点，而 11 则是它的右子结点。

我们再来分析一下另一个数组｛7，4，6，5｝。后序遍历的最后一个树是根结点，因此根结点的值是 5。由于第一个数字 7 比 5大，因此对应的二叉搜索树中，根结点上是没有左子树的，数字7，4 和 6 都是右子树结点的值。但我们发现在右子树中有一个结点的值是 4，比根结点的值 5 小，这违背了二叉搜索树的定义。因此不存在一颗二叉搜索树，它的后序遍历的结果是7，4，6，5。

show my code

/**
 * 判断一个序列是否为二叉搜索树的后序遍历序列
 * @author innovator
 *
 */
public class VerifySquenceOfBST {
    
    /**
     * 判断一个整数序列是否为二叉搜索树的后序遍历序列
     * @param squence
     * @param length
     * @return
     */
    public static boolean verifyIntSquenceOfBST(int[] squence,int length){
        
        if(squence == null || squence.length == 0){
            return false;
        }
        
        /**
         * 二叉搜索树的性质：
         * 左子树不为空，左子树的左右结点值均小于根结点值
         * 右子树不为空，右子树的左右结点值均大于根结点值
         * 左右子树也为二叉搜索树
         */
        
        //后序遍历的根结点就是序列最后一个值
        int root = squence[length-1];
        
        //遍历序列找到左右字树区分的位置，二叉搜索树中左子树均小于根结点，且最后一个肯定是根结点的左孩子
        int i = 0;
        for(; i root){
                break;
            }
        }
        
        int j = i;
        //判断右子树的值是否合法
        for(; j< length-1; j++){
            if(squence[j] <= root){
                return false;
            }
        }
        
        //判断左右字树是否为二叉搜索树
        boolean left = true;
        //左子树的长度大于0
        if(i > 0){
            //递归验证
            left = verifyIntSquenceOfBST(squence, i);
        }
        
        boolean right = true;
        //右子树有元素
        if(i < length -1){
            // 递归验证,构造右子树序列
            int[] rightSquence = Arrays.copyOfRange(squence, i,length-1);
            right = verifyIntSquenceOfBST(rightSquence, rightSquence.length);
        }
        
        return left && right;
    }

    
    public static void main(String[] args){  
        
        int[] s = {
                5,7,6,9,11,10,8
        };
        System.out.println("是否为二叉搜索树的后序遍历序列："+verifyIntSquenceOfBST(s, s.length));
    }
}

结果